基于改进卷积神经网络的无绝缘轨道电路调谐区故障诊断

田粉霞，杨世武，崔 勇，武 沛

（北京交通大学 电子信息工程学院， 北京 100044）

截至2019 年底，我国高速铁路里程已达3.5 万km。作为高铁基础设备，ZPW-2000 系列无绝缘轨道电路完成全线列车占用检查，并向车载设备发送连续信息，其功能完整性直接影响列车安全和运行效率，其故障诊断的实时性具有重要意义。在轨道电路故障诊断方面已开展了较多研究[1-2]。调谐区作为实现相邻两轨道区段轨道电路信号的隔离，且该部分设备在轨旁1.5 m 的位置[3]，受列车震动以及环境影响，极易发生故障。当调谐区设备发生故障时，相邻两区段的信号会发生混频，机车可能接收到相邻轨道区段的信号，造成错误解码，从而影响列车安全运行。当列车占用区间的发送端调谐区设备故障时，列车可接收运行前方区段的轨道电路信号，最严重情况下可能发生列车追尾事故；当列车占用区间的接收端调谐区设备故障时，列车可接收运行后方区段的轨道电路信号，最严重情况下可能导致本区段及后方区段列车停车，影响行车效率。因此，调谐区设备是否正常运行对列车运行安全及效率将产生直接影响。

文献[4-5]采用神经网络实现调谐区设备的故障诊断，其特征提取方法是通过对前4 个补偿电容区间内的信号进行曲线拟合，将拟合结果输入到神经网络实现故障分类，其前期特征提取过程较复杂；文献[6]采用定性趋势分析的方法，当噪声较小时诊断正确率可达到96.3%，当信噪比达到40 dB 时，诊断正确率降至65.4%，其诊断结果易受噪声的影响；文献[7]针对小波阈值去噪可能造成直接去除故障信号中较小幅度信号的影响，通过CEEMD 方法进行轨面电压信号的特征提取，但仅提取故障特征，需要与分类算法结合，才能实现故障诊断。

深度学习工具-卷积神经网络能同时实现特征提取及特征分类，且分类准确率高，在语音识别、图像处理、自然语言处理、信息抽取及故障诊断中应用广泛[8-10]。鉴于调谐区设备故障对机车信号电压的影响与图像分类中边缘特征的提取相类似，因此本文采用卷积神经网络来实现调谐区设备的故障诊断，该算法可以在集中监测设备上实现，当设备未发生完全松断时便可预测诊断出故障隐患，实时性及预防效果较好。

1 机车信号电压模型及调谐区故障影响分析

1.1 车地结合故障诊断方案

利用轨道电路地面采集的数据，信号集中监测系统只能实现部分故障的诊断。为实现完整的故障诊断，需进一步结合车载设备采集的数据。机车采集的数据存储在车载列车运行监控记录装置LKJ 中，通过无线通信，可将这些数据传输至地面设备，由地面设备完成故障诊断，车地结合故障诊断[4，11]的实现过程如图1 所示。

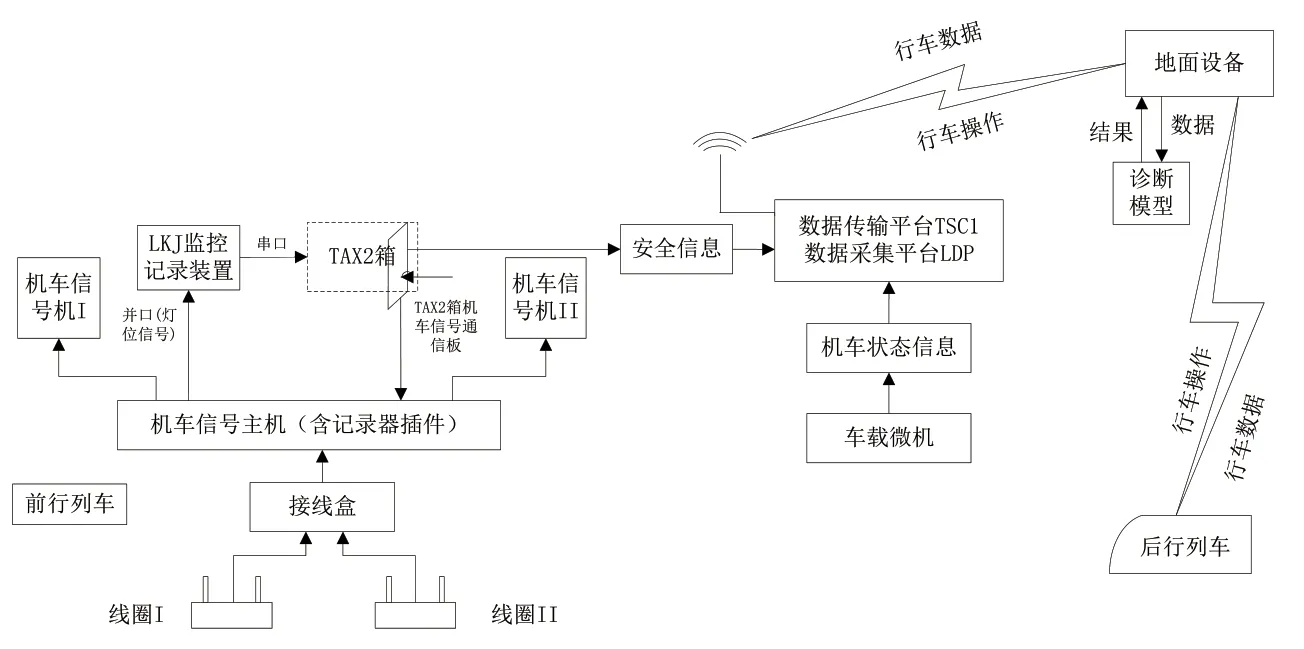
图1 车地结合故障诊断示意

1.2 机车信号电压模型

为获取机车信号电压，建立分路状态下机车信号电压模型[12-14]，如图2 所示。

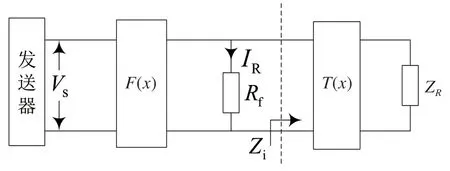
图2 分路状态下机车信号电压模型

图2 中，Vs为发送器输出电平；x为分路点在钢轨的位置；F(x)为发送器至分路点间设备的四端网传输矩阵；IR为分路电流；Rf为分路电阻；T(x)为分路点至接收端的传输矩阵；ZR为接收器的输入阻抗；Zi为分路点向接收端的输入阻抗。

机车分路电流为：

机车信号电压为：

其中，α为接近于常数的系数。

通过仿真得到调谐区无故障时机车信号电压，如图3a 所示；现场从LKJ 中截取的波形如图3b 所示，信号-时间关系曲线可通过采样频率与速度的关系转换为信号-位置关系[6]。由图3 可知，仿真值与现场数据基本一致；由于仿真模型中发送端到接收端的方向与现场的方向相反，因此波形的趋势相反。

1.3 故障模式对机车信号电压的影响分析

不同故障模式（BA2、SVA、BA1）下机车信号电压如图4 所示。仿真实验获取的数据中，各类故障模式的严重程度见表1。

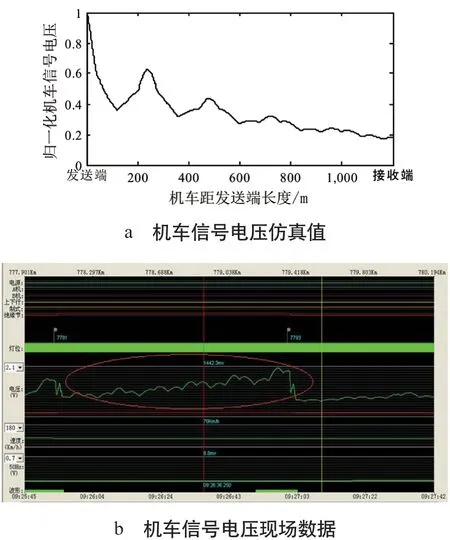
图3 机车信号电压

图4 不同故障类型时机车信号电压

表1 故障模式严重程度

考虑到机车信号电压补偿电容故障及道砟电阻大小等因素的影响，对数据集进行扩充，以补偿电容C3 及C9 故障为例说明，如图5a 所示。不同道砟电阻对机车信号电压的影响如图5b 所示。

图5 不同现场条件对机车信号电压的影响

由调谐区的结构组成可知，调谐区4 种故障模式对应CNN 分类层4 个输出神经元的输出；激活函数输出值为1 时，则输入信号属于该类故障；激活函数输出值为0 时，激活函数不属于该类故障。调谐区4 类故障模式对应的编码见表2。

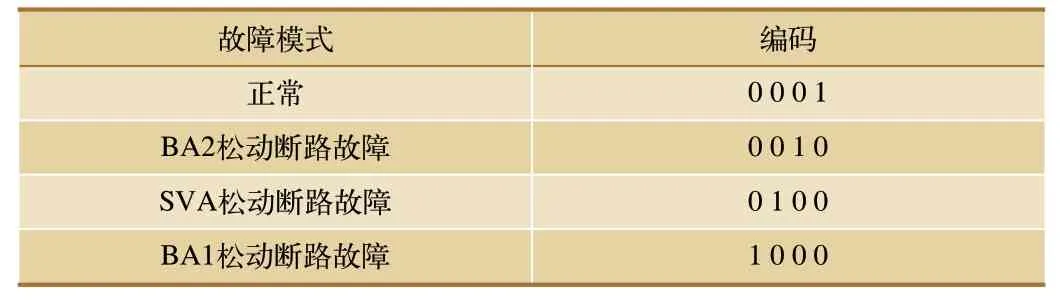
表2 故障模式编码

2 卷积神经网络

相对于前馈神经网络及BP 神经网络，CNN 在输入层后增加了卷积层及池化层，用来实现输入信号的特征提取及降维。采用BP 神经网络实现调谐区的故障诊断时，若直接将采集信号输入到算法中，会导致节点数量多，算法复杂度上升，内存占用率高；若降低输入信号的维度，则需要人为确定故障特征显著的区域， 并通过拟合等方法确定故障特征，数据前期处理过程较为繁琐。通过CNN 实现故障诊断时，卷积层可实现输入信号的特征提取，并通过设置池化层参数实现输入信号的降维。

2.1 特征提取

试验中区间轨道电路每隔1 m 生成一组数据，卷积神经网络单个输入数据维度为1×1 200，输出信号的维度为1×w；其中，w的计算公式为：

其中，m为卷积核的大小，p为补零的圈数，s为卷积层的采样步长。输出信号值的计算公式[10]为：

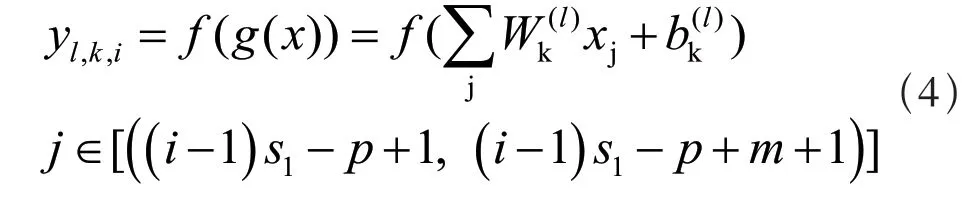
yl，k，i为第l 层卷积层第k个卷积核的第i个输出，W为第l 层卷积层的第k个卷积核的权值，xj为第l层卷积层的输入信号，为第l 层卷积层的第k个神经元的偏置。卷积层的激活函数f常采用relu 函数：

原始输入数据经卷积层进行特征提取后，其特征向量维度较高；因此，在尽量保持原特征的条件下，通过池化层降低特征向量的维度。常用的池化层方法有平均池化、最大池化和重叠池化，本文选择最大池化。若池化层的采样步长为s2，池化的区间大小为k2，输出信号的维度为1×((w+2p)/s2)，则第S层池化层中输入为第k个卷积核的输出的第j个输出值的计算公式为：

2.2 故障分类

池化后特征向量的维度通常大于分类层输入信号的维度。因此，池化后增加全连接层，以实现池化层到分类层的维度转换。分类层通过softmax 函数实现输入特征的分类，函数形式为：

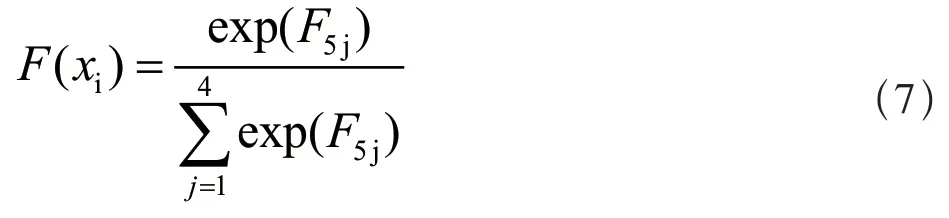
其中，F(Xi)为输入信号xi属于每种故障的概率值，各元素之和为1，F5j为全连接层的输出。

通过目标函数的最小化实现权值及偏置的优化，目标函数为：

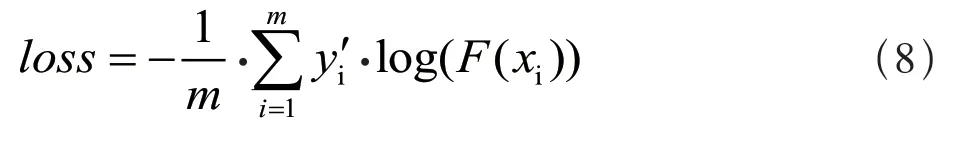
其中，y′i为实际标签中的第i个值。

权值及偏置的更新过程分别为式（9）和式（10）：

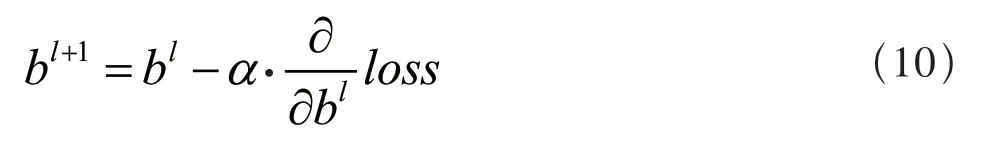
其中，α为学习率。为保证快速得到一个较优的解，开始训练时使用较大学习率，然后通过迭代逐步减小学习率，使模型在训练后期更加稳定；加入指数衰减学习率，其计算公式为：

其中，α0为初始学习率，取值范围为[0，1]；r为衰减系数；c为当前迭代次数；s为衰减速度。

鉴于输入信号维度较高，采用两层卷积层及两层池化层实现输入信号的特征提取；第2 池化层后连接两层全连接层，第1 层全连接层实现特征向量到输出向量间的个数转换，第2 层全连接层用来实现故障分类。在模型训练过程中，采用dropout 函数提高模型的泛化能力，防止模型出现过拟合，同时减少需要训练的参数，可缩短模型的训练时间。

3 仿真实验与诊断结果分析

通过Matlab 仿真，获取轨道电路正常情况下以及不同故障在不同故障严重程度条件下的数据总共2 112 条，仿真实验中相关参数设置见表3。训练集数据越多，模型精度越高。因此，按照训练集：测试集=9：1的比例对模型进行训练，训练步骤为1 500步，初始学习率为0.001。

表3 测试参数设置

基于TensorFlow 框架实现CNN，仿真及训练过程中使用的计算机处理器为Intel(R) Core(TM)i5-4200U CPU@1.60 GHz。

3.1 减小错误标签对诊断结果的影响

故障诊断中使用的数据集标签是人为标记的，因而难免存在数据标签错误的情况。当上述情况发生时，loss 值较正常值偏差较大，会对参数的学习过程产生影响，如图6 所示。

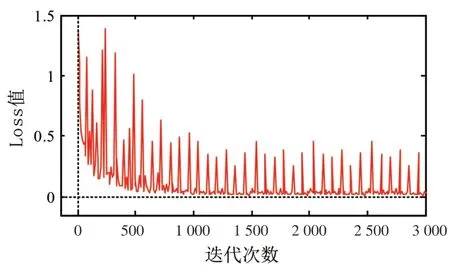
图6 含错误标签数据的损失函数变化

numpy 中的remove 函数无法删除二维数组中的一维数据，因此采用构建错误标签数据集的方法，可减小错误标签数据对训练过程的影响，实现流程如图7 所示。

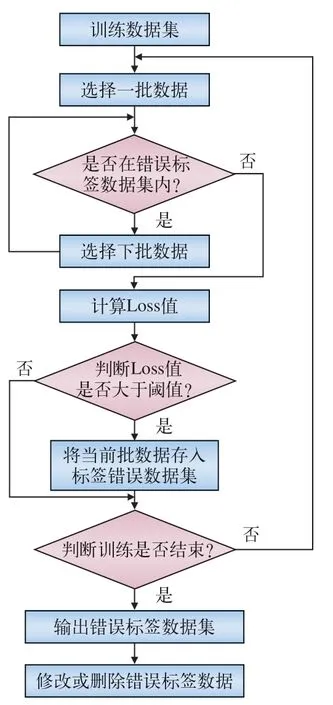
图7 训练集中错误标签数据识别流程

训练过程中加入图7 所示的流程后，Loss 值的变化如图8 中曲线l1 所示，波动明显减小，消除了错误标签在下一次训练过程中对训练过程的影响；曲线l2 为删除上述错误标签数据后的Loss 图。由图8 可知，两条曲线基本一致，即可以减小错误数据标签对诊断结果的影响。

图8 去除错误标签数据损失函数变化

3.2 减小错误标签对诊断结果的影响

在CNN 中，特征提取通过卷积层实现，卷积核的个数、大小及采样长度对诊断准确率及模型训练时间有直接影响。因此，通过对该些参数的对比分析，选择当前条件下最优的参数。

3.2.1 卷积核个数对诊断结果的影响

当卷积核大小为1×2，采样步长为1×1，不同卷积核个数时的诊断结果见表4。

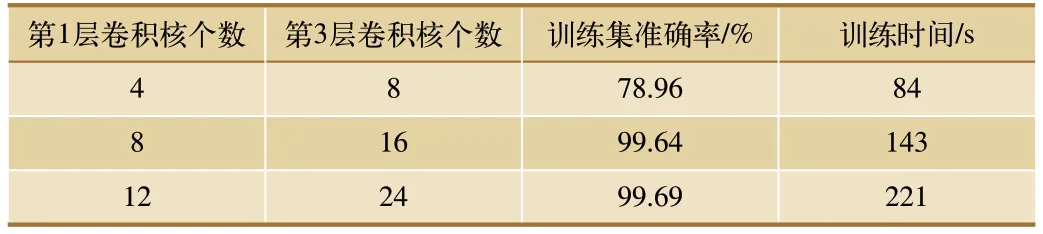
表4 卷积核个数对诊断结果的影响

由表4 可知，当第1 层（第1 卷积层）和第3 层（第2 卷积层）的卷积核个数分别大于8 和16 时，诊断准确率基本保持不变，训练时间变长，即算法复杂度的继续增加对诊断结果无正向影响；因此，第1层和第3 层的卷积核个数分别选择为8 和16。

3.2.2 卷积核大小对采样结果的影响

当第1 层（第1 卷积层）和第3 层（第2 卷积层）的卷积核个数分别为8 和16、采样步长为1×1 时，不同卷积核大小对应的诊断结果见表5。

表5 卷积核大小对诊断结果的影响

由表5 可知，卷积核越大，需要训练的参数越多，模型训练的时间越长，且卷积核越大，容易造成局部特征的损失，故障诊断准确率降低。

3.2.3 采样步长对诊断结果的影响

当第1 层（第1 卷积层）和第3 层（第2 卷积层）的卷积核分别为8 和16、卷积核大小为1×2 时，不同采样步长对应的诊断结果见表6。

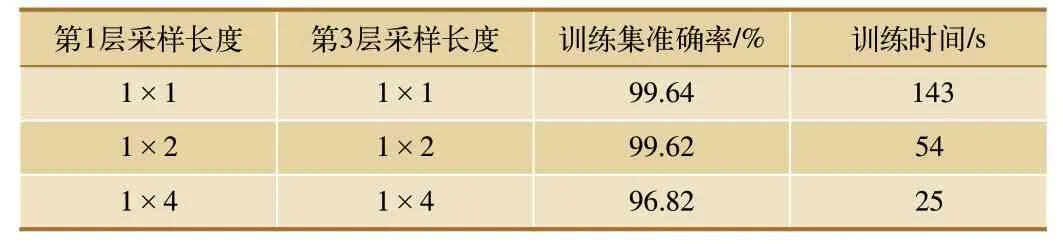
表6 采样步长对诊断结果的影响

由式（3）可知，采样步长对卷积层输出信号维度的影响按比例变化；当采样步长变长时，输出信号的个数减少，可训练参数的个数也减少，算法的复杂度降低，训练时间迅速减少，但输入信号及第1层池化层的局部特征量损失严重，诊断准确率降低。

通过对比分析上述参数，在保证诊断准确率的条件下，为降低算法复杂度，缩短模型训练时间，最终确定卷积层的参数为：第1 层（第1 卷积层）的卷积核个数为8，大小为1×2，采样长度为1×2；第3层（第2 卷积层）的卷积核个数16，大小为1×2，采样步长为1×2。对应的卷积神经网络模型如图9 所示。

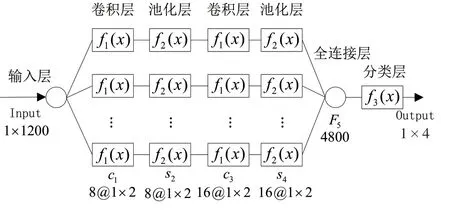
图9 卷积神经网络模型

图9 中，f1(x) 为卷积层激活函数，本文采用ReLU 函数；f2(x) 为池化层运算函数，本文采用Max_pool 函数；全连接层F5中增加Dropout 函数，以防止模型在训练过程中出现过拟合，神经元被选中的概率值设置为0.5；f3(x)为分类层激活函数，本文中用softmax 函数。当信噪比为60 dB 时，诊断结果见表7。

表7 训练集及测试集诊断结果

3.3 不同干扰环境下的诊断结果

由表8 可知，当SNR=60 dB 时，测试集诊断准确率可达到98.96%。由于轨道电路读取器（TCR，Track Circuit Receiver）通过电磁感应的方式接受轨道电路中的差模信号电流，易受不平衡牵引电流及环境噪声的影响，因此对比分析不同信噪比条件下的诊断准确率。

由表8 可知，卷积神经网络对噪声具有较强的承受能力，在上述仿真实验条件中，当噪声由60 dB增大到40 dB 时，测试集诊断正确率下降约为1%，即在噪声干扰条件下，测试数据仍具有较高诊断正确率。

表8 信噪比对诊断结果的影响

4 结束语

采用卷积神经网络对轨道电路调谐区进行故障诊断研究，得出如下结论：

（1）在补偿电容故障、不同道砟电阻的情况下仍然能识别出故障。针对现场不同道砟电阻及可能出现的补偿电容故障对机车信号电压的影响，对机车信号电压数据集进行补充，诊断结果表明算法可以实现不同环境下故障模式的识别。

（2）错误数据标签的处理。对算法进行训练的数据是人为标记的，其中可能存在故障数据与标签不一致的现象，对模型参数训练及诊断准确率均会造成影响。通过建立错误标签数据集，并在下一次训练过程中剔除该数据集，可以减小错误标签的影响，诊断结果表明该方法的有效性。

（3）噪声环境下故障诊断的有效性。TCR 通过电磁感应的方式获取轨道电路信号，会受到不同程度噪声的影响；对不同噪声程度下的故障进行分类，结果表明：当噪声达到40 dB 时，诊断准确率为97.92%，即该诊断方法对噪声具有较强的承受能力。