路面基层级配碎石填料永久变形特性试验研究

蒋 旭

(中交第三公路工程局有限公司第四工程分公司，重庆 404100)

1 研究背景

当前国内广泛采用的沥青路面基层结构型式仍以半刚性基层为主，然而半刚性基层沥青路面服役期间易出现各类病害，主要包括基层的收缩开裂导致的沥青路面渗水，水的入渗可加剧路面各类病害的严重程度；排水性能不佳的半刚性基层容易在行车荷载重复作用下引发翻浆冒泥等病害，造成路面破坏并危及行车安全；半刚性基层在高周频次重复车辆荷载作用下还容易发生疲劳破坏，而半刚性基层路面结构的特点决定了这类基层的维修难度大、成本高。

为克服半刚性基层路面病害问题，同时也为了拓宽国内路面结构设计的选择，越来越多的国内研究者[1-2]开始重视在国外道路路面基层与底基层中普遍采用的级配碎石柔性基层。作为散粒体材料，级配碎石拥有良好的排水能力，能够避免由动水压力引起的路面病害。此外，级配碎石基层具有良好的耐久性、温湿度引起的体积变化稳定性和养护维修的便易性等优势。

级配碎石基层和底基层在行车荷载重复作用下产生的累积塑性变形是制约其在道路工程中应用的主要因素，也是柔性路面结构设计中普遍采用的结构性破坏评价指标。目前国内对级配碎石材料的动力特性研究还十分匮乏，基层设计状态与实际应用状态之间往往存在较大的偏差，因此，有必要针对级配碎石在高周频次重复荷载作用下的累积塑性变形特性展开深入研究。

本文首先针对用于基层和底基层的级配碎石填料开展了静三轴剪切试验，从而获取材料的抗剪强度和静力破坏强度包络线。随后以最小平均主应力pmin和偏应力幅值qmax作为试验变量，开展了一系列重复加载动三轴试验，探究试样在不同应力状态下的轴向累积塑性应变规律。

2 三轴剪切试验设计

2.1 试验材料

试验所采用的材料来自柔性路面常用的级配碎石，其中基层材料为机制石灰岩砾石，底基层材料为人工筛选碎石。两种级配碎石材料的基本物理指标值如表1所示。

表1 基层和底基层级配碎石基本物理指标值

2.2 试样制作与试验仪器

静态三轴试验采用直径和高度分别为150 mm和300 mm的圆柱体试件，重复加载动三轴试验采用直径和高度均为150 mm的试件。试样制作过程参照《公路土工试验规程》(JTG E40-2007)[3]中相关内容进行。

试验采用自主研制的重复加载动三轴仪，该仪器具备进行复杂应力路径下重复加载三轴试验的功能。

3 静三轴剪切试验

由于级配碎石的抗剪强度特性几乎不受加载路径和加载速率等的影响，因此可以通过静力加载破坏性试验获取级配碎石的破坏强度包络线。为此，分别在34.5、69.0、103.5 kPa围压下对相同条件的试样进行静三轴试验，根据试样破坏时的峰值偏应力值绘制抗剪强度包络线。联立解算得到级配碎石的抗剪强度参数值，基层与底基层的似粘聚力分别为132.3、182.0 kPa，两者内摩擦角分别为61.7°、43.9°。

4 动三轴剪切试验

4.1 试验原理与方案

对于级配碎石基层或底基层中的任意单元体而言，除了承受自重应力等短期内不会发生变化的应力，还会由于行车移动荷载的作用而承受周期变化的附加应力，即单元体各项应力状态参数的量值与方向发生周期变化。这意味着级配碎石基层或底基层单元体所受应力分量包含了静应力和动应力的成分。

动三轴试验的试样应力状态参量中，最小偏应力qmin和最小平均主应力pmin反映了由重力引起的土单元静应力成分；偏应力幅值Δq和平均主应力幅值Δp反映了由移动行车荷载引起的土单元动应力成分。

为探究试样在不同应力状态下的轴向累积塑性应变规律，本文以最小平均主应力pmin和偏应力幅值qmax作为试验变量，开展了一系列重复加载动三轴试验。其中，偏应力施加方式为半正弦波形的轴向循环荷载，波形周期为0.1 s，相邻波之间的间隔休止期为0.9 s。试验计划如表2所示，其中应力路径长度L由式(1)给出：

(1)

表2 常围压动三轴试验加载方案

应力状态参数中，应力路径坡度m和应力路径长度L反映了动态加载过程中的加载应力路径。

4.2 试验结果

动三轴试验条件下基层和底基层级配碎石填料试样的轴向累积塑性应变随循环加载次数变化曲线分别如图1～2所示。其中，图1～2右上角图例的数值分别代表了围压σ3(kPa)和轴向动偏应力幅值σ1d(kPa)。动三轴试验的循环加载次数均为10 000次。试验过程中由于部分试样意外破坏，因此，表2～3中所列出的试验计划中有部分未能获取有效数据。

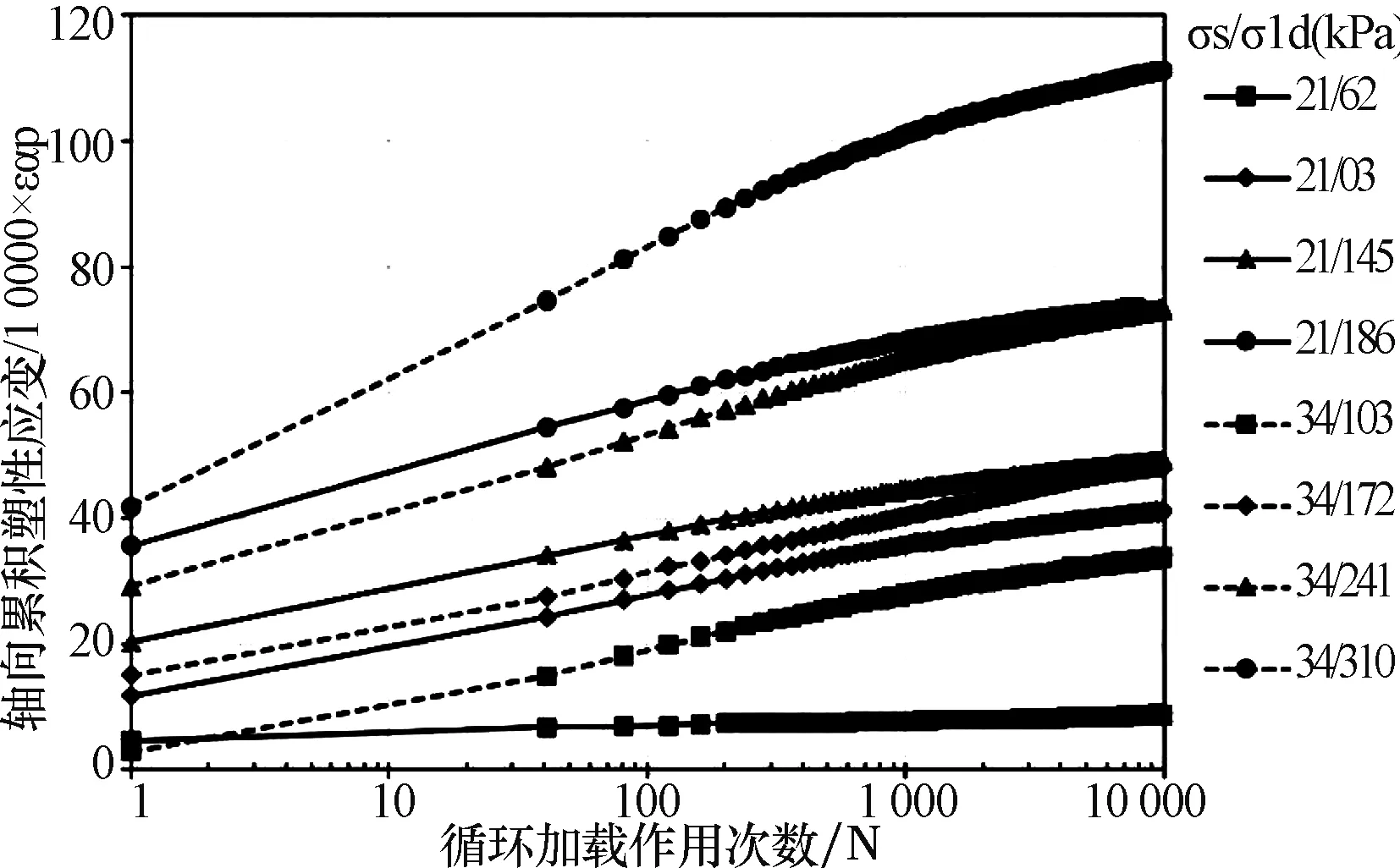
图1 基层级配碎石轴向累积塑性应变

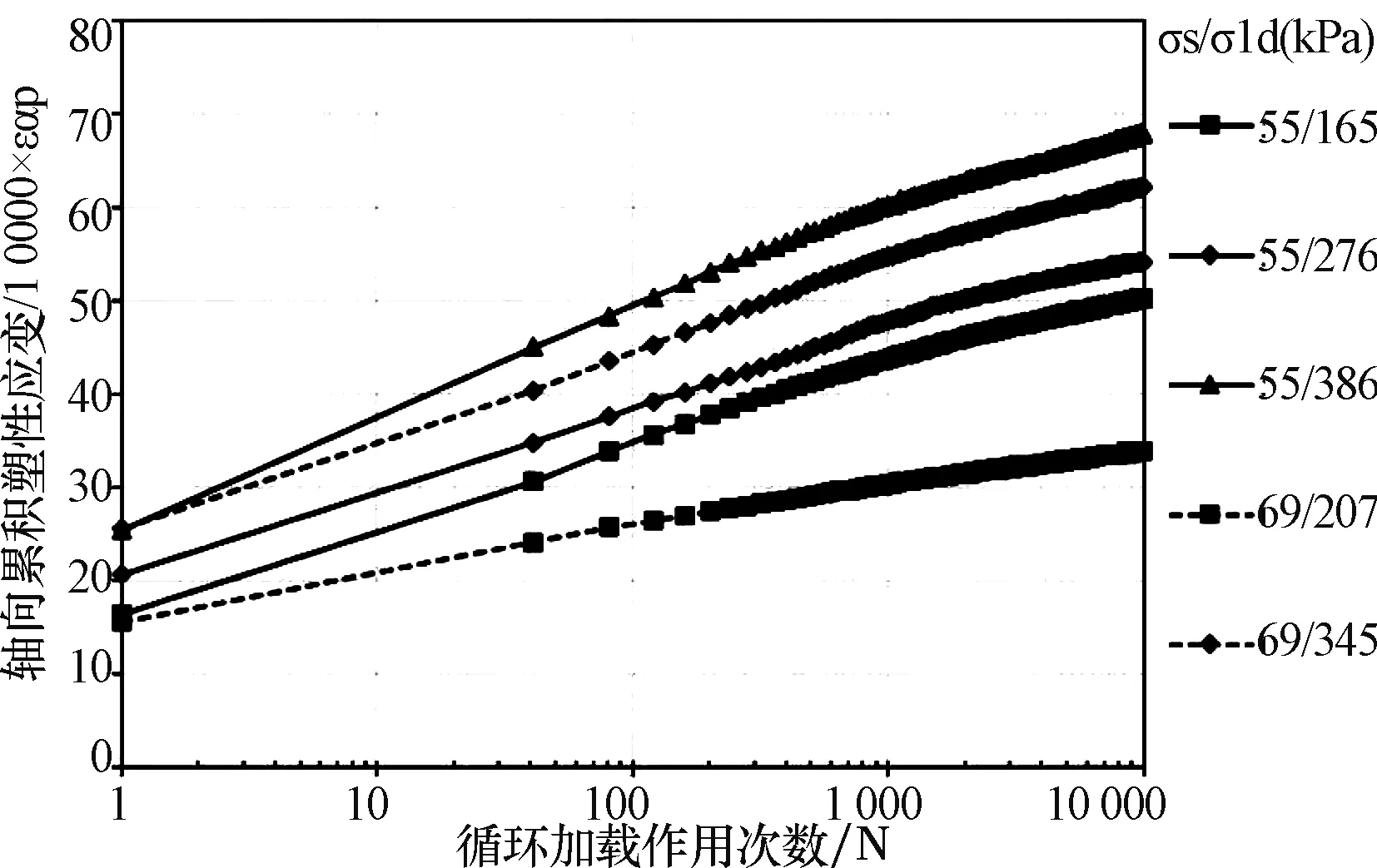
图2 底基层级配碎石轴向累积塑性应变

由图1～2可见，随着围压σ3的减少、轴向偏应力Δq的增加，轴向累积塑性应变值及其累积速率呈现上升趋势。

4.3 安定状态分析

以级配碎石为代表的散粒体材料永久变形发展趋势可划分为塑性安定(A区)、塑性蠕变(B区)和增量破坏(C区)这三类动力行为类型。

欧洲标准中的安定状态判定准则以第3 000次和第5 000次循环加载时的轴向累积塑性应变值之差Δεapw作为动力行为类型的评价标准，如下所示：

A区：Δεapw<4.5×10-5

B区：4.5×10-5<Δεapw<4.0×10-4

C区：Δεapw>4.0×10-4

Δεapw=Δεap,5000-Δεap,3000，其中，Δεap,3000和Δεap,5000分别表示第3 000次和第5 000次循环加载时的轴向累积塑性应变值。

根据这一评价标准，计算得到本次循环加载试验中各试样第3 000次和第5 000次循环加载时的轴向累积塑性应变值之差，并据此判定其安定状态分区情况，如表3所示。

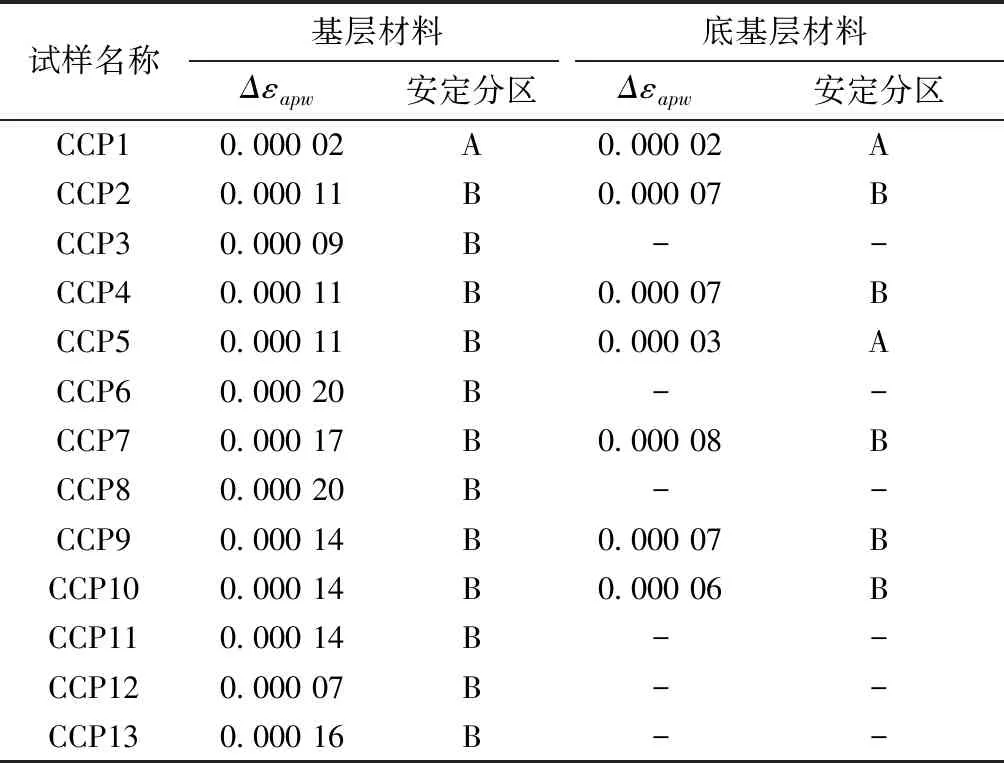
表3 动三轴试验结果的安定状态分区

如前所述，常围压循环加载试验中以最小平均主应力pmin和动偏应力幅值qmax作为试验变量，因此，在建立散体材料安定状态判定参数值的预测模型时，除了需充分考虑变围压循环加载条件下试样的应力状态，仍需包括常围压条件下的相应变量。

基于上述考虑提出预测模型如式(2)所示：

Δεapw=A×(Pmin)B×(qmin)C

(2)

式中，pmin和qmax分别为最小平均主应力、偏应力幅值；A、B和C均为回归系数。

利用式(2)拟合所求Δεapw值及其相应的应力状态参数，得到基层和底基层级配碎石材料的回归系数如表4所示。

表4 基层和底基层级配碎石材料拟合回归系数

表4中拟合确定系数R2值反映了式(2)拟合效果良好。回归系数值反映了最小平均主应力pmin与Δεapw值呈负相关；偏应力幅值qmax与1/as值呈正相关。这表明pmin的增加使得轮载重复作用下级配碎石永久变形行为在一定程度上趋于安定，而qmax的增加则导致相应的永久变形行为趋于加速增长。

5 结束语

在以最小平均主应力和pmin偏应力幅值qmax作为试验变量开展的一系列基层和底基层级配碎石动三轴试验中，验证了pmin的增加使得轮载重复作用下级配碎石永久变形行为在一定程度上趋于安定，而qmax的增加则导致相应的永久变形行为趋于加速增长。研究成果可为国内级配碎石基层和底基层在行车荷载重复作用下产生的累积塑性变形评价指标的建立提供有益的参考。

[ID:009747]