热分析动力学研究方法的新进展
任宁,王昉,张建军,郑新芳
1邯郸学院,化学化工与材料学院,河北省杂环化合物重点实验室,邯郸 056005
2南京师范大学,分析测试中心,南京210023
3河北师范大学,分析测试中心,化学与材料科学学院,石家庄 050024
1 引言
热分析是在程序控温(和一定气氛)下,测量物质的某种物理性质与温度或时间关系的一类技术。热分析动力学是以热分析技术为基础,综合运用化学热力学、动力学和相关学科知识,研究物质的物理变化和化学反应速率以及机理的一门分支学科1。利用热分析动力学,可以确定高聚物等材料的热稳定性和使用寿命,评价药物的稳定性,评定含能材料易燃易爆物质的危险性,同时,可以研究无机物质脱水、分解、降解或配合物解离机理,估计环境污染物质的分解情况等1。
在研究固相反应中,热分析动力学研究有很多数学模型和相应的数据处理方法。从大类上分为等温法和非等温法,从动力学方程形式上分为积分法和微分法,从操作方式上分为单一扫描速率法和多重扫描速率法(等转化率法)2-4。由于单一扫描速率法不能完全反映固态反应的复杂本质,国际热分析与量热学协会(ICTAC)呼吁使用多重扫描速率法测定热分析数据5-7,同时,采用等转化率法确定活化能随转化率的变化情况,从而揭示看似简单反应实际为复杂反应的本质。早在19世纪50-60年代,Flynn-Wall-Ozawa (FWO)8,9、Kissinger-Akahira-Sunose (KAS)10和Friedman11等就提出了最具有代表性的等转化率方法。目前,有很多研究者使用以上方法进行固相反应热分析动力学的研究12-18。其中Flynn-Wall-Ozawa (FWO)法的使用率在所有等转化率法中占比高达80%19。但是传统的等转化率方法在计算活化能时有很大的误差。例如Ozawa法的计算结果的准确性是受到E/RT取值的范围的影响(20 ≤E/RT≤ 60),Ozawa和Kissinger法忽略了H(x)和h(x)随x(E/RT)取值的变化等1。
基于以上传统方法的局限性,19世纪90年代以来,热分析工作者提出了很多种可以精确计算反应活化能和推断机理函数的不等温等转化率方法。如:Starink方程20、Vyzaovkin法21,22、Li-Tang法23、非线形等转化率微分法(NL-DIF method)24、非线形等转化率积分法(NL-INT)25、Popescu法26、双等双步法27及张建军等人改进的Popescu法28等。有关以上各种等转化率方法的成功与局限,详见陆振荣3、席国喜29、任宁及张建军4等人的综述。同时,国外学者Vyzaovkin19,30-33、Burnham34、Mija35、Criado36等人从数学计算复杂性、方程适用性、活化能计算准确性及应用性等方面,也对提出的各种等转化率方法进行了科学地评价。
近十年来,国内外又有很多新的等转化率方法被提出或者改进,并广泛应用于研究固相反应的热分解动力学方面。仅2012-2014三年间,有近2000篇论文是用等转化率法进行动力学分析的19。
限于篇幅,本文仅综述近十年来提出的一种新的动力学方程和几种新的等转化率方法,作为以往热分析数据处理方法研究综述3,4,29的补充。热分析动力学的理论基础详见相关综述报道3,4,29。
2 一种新的动力学方程
对于非等温过程中的动力学方程,正确的Arrhenius方程的温度积分应该是从T2到T1(单位为K),但是许多动力学方程的温度积分是从T到0 K,研究表明对于某些反应,这些方程中的活化能存在很大的误差。成一37提出了一个新的动力学方程,用等转化率法可以精确求解线性或非线性加热过程中化学反应的活化能。
新方程为:
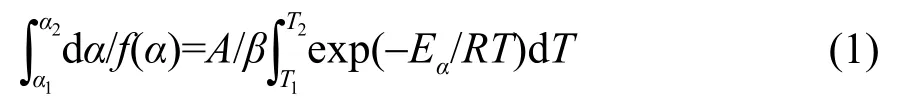
这里的α为转化率f(α)是机理函数,A是指前因子,β是升温速率,Eα是活化能,R是摩尔气体常数,T是温度(K)。
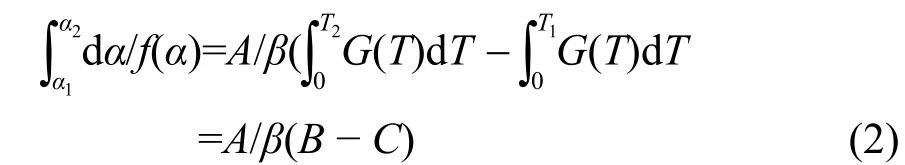
对于一个非等温的反应过程,假设机理函数f(α)在某一温度范围内无变化,在不同升温速率下,对与任意给定的两个转化率,的值都是一个常数,即

因为A是一个常数,这样方程(2)转化为

对于任意两个升温速率下的热重曲线,方程(4)可以写为:

假设一个活化能E的值,则B和C的近似值可用下式计算:
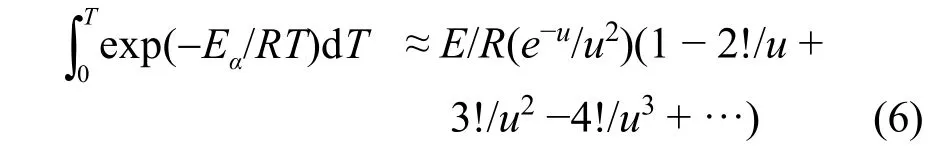
这里的u=E/RT。
通过B和C的值即可得到式子β/(B−C)的比值,如果在不同升温速率下该比值不是一个常数的话,可以改变活化能的数值,直到不同升温速率下该式子的比值相等或者差值最小时,可以认为该活化能为即为精确值。
该方程的优点是即可以适用于从T到0 K积分时反应过程平均活化能的计算,也可以计算当两个转化率差值极小时,即点到点的活化能。实验结果表明,新方程得到的活化能较Ozawa方程更准确。不过,此方法还需得到更进一步的验证。
此外,考虑到热传导是热分析中不可忽略的主要因素,成一建议了一种含有热传导因素的动力学方程38,并对方程进行改进,可以测得不同升温速率下的多条DTA曲线的峰温处的活化能。实验结果表明,利用热传导动力学方程可以明显减少活化能的偏差。
3 几种新的等转化率方法
3.1 平均线性积分法
2008年Ortega39提出了一种简单而精确的平均线性积分法。他认为使用从0到α的简化积分,不适用于确定活化能E对转化率α的变化关系。这里提出的平均线性积分法是在一个很小的转化率范围内进行积分,避免了它的使用局限性。如改进的等转化率方法一样,也是在一个很小的范围内对速率方程进行积分控制。因此对于很小的Δα范围内,可以利用“平均值”定理来近似温度积分。

在一个很小的范围内(α −Δα,α),E和A的值可以认为是一个常数,结合动力学积分方程

变为:

由方程(11)的对数形式可以求出不同升温速率下的活化能数值。因为大多固态反应不是一步简单的反应,该方法的优点是可以通过活化能E随转化率α的关系揭示反应的复杂性。此外,新方法是基于对时间的积分,在任何加热程序条件下都可以使用。最近,Rotaru等人40对Ortega法进行了改进,提出用代替方程(11)中的Tα,并且针对恒定升温速率下单步过程的模拟数据,讨论了这种替代对测定的活化能E值的影响。同时Ortega A还提出了一个可以估算指前因子A以及推断机理函数G(α)的方法。应用补偿效应(lnAα =mEα + n)估算指前因子A,则方程(11)可以转变为方程(12):

如果假设最初的反应机理模型没有变化,通过方程(12)的截距可以得到:

这里I代表截距。
代入各种机理函数模型1,根据得到方程(13)的最佳相关性,选择最可几的机理函数。利用线性回归计算补偿参数m和n的值,由此可以获得指前因子A的数值。
3.2 迭代线性等转化率积分法
当活化能随转化率的变化较大时,传统的线性积分等转化率方法在测定活化能时可能会产生重要的误差。2001年,Vyazovkin41提出了一个改进的非线性等转化率积分法(MNL-INT),从而求得更精确的活化能的数值。但是该方法计算比较耗时,基于此蔡均猛等人42提出一个新的迭代线性等转化率积分法,该方法是由基本的动力学速率方程推导而来,没有任何假设。其优点是即便活化能对转化率变化很大,也能计算出有效的活化能数值,而且比Vyazovkin法用时短。基本原理如下,转化非等温非均相反应的动力学方程为:

第二步:再用Eα(1)值计算下式
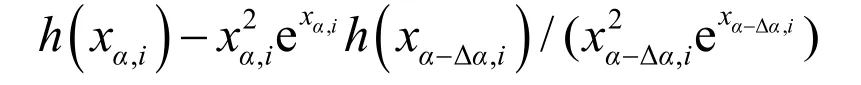
重复第一步,由斜率求得一个新的Eα(2)值。经过几次迭代后直到∣Eα(1)−Eα(1)∣<ε(0.001 kJ·mol−1),即得到准确的活化能值。通过迭代法求得的活化能还可以用来确定[Aαf(α)]随转化率变化的函数式。

Eα和[Aαf(α)]的值可以通过MATLAB程序软件,用线性迭代等转化率积分法求得。该法适合研究物质快速热解的燃烧动力学行为。
3.3 步进式新等转化率方法
刘乃安等人43认为在Li-Tang法23和Budrugeac改进的Li-Tang方法44推导过程中,反应的活化能是不随转化率而变化的。否则从0或者α1到求解值α将导致系统误差。然而,需要强调的是,反应活化能在一个很小的积分区间 Δα内变化是很小的,那么在 Δα范围内积分方程可以转化为:

在上式中,α在3Δα/2到1 − Δα/2之间以Δα =1/(m+1)为步长变化,其中m是变化区间的取点数目。
显然,步进式方程(16)克服了LT法和Budrugeac改进的方法求解反应活化能依赖于积分下限的问题。并且步进式新等转化率方法也避免了由于温度积分近似式的引入而导致活化能系统误差的问题。通过实验验证,新方法可以得到和Friedman方法11和改进的Vyazovkin方法41一致的结果。
3.4 用于单一活化能计算的新的等转化率方法
该方法45同时具有拟合法和等转化率法的系统优点,能够获得比使用拟合法更可靠的单一活化能的数值。
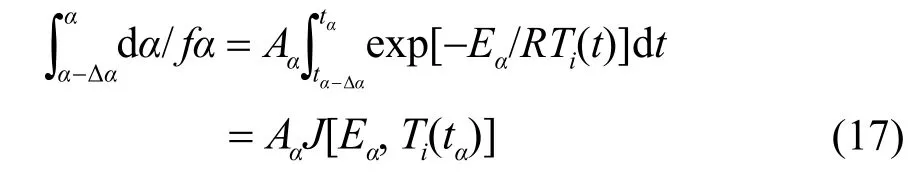
根据改进的Vyazovkin方法提出的方程(17),则对于某一特定的转化率α的n组任意升温速率实验可得:
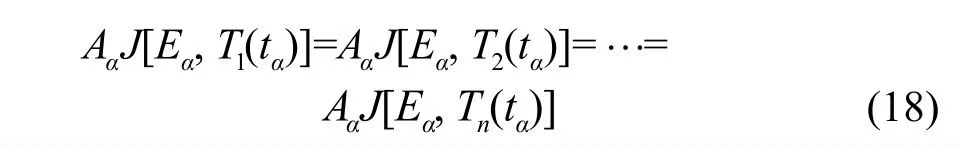
约去Aα,代入特定转化率所对应的温度Tα和时间tα,使下式(19)的E值达到最小时,即为特定转化率下的活化能的值。

显然,该方法的优点是求解过程没有预先设定反应机理模型,并且没有采取任何的假设条件。通过实验数据验证,该方法对实验噪音有良好的容许度,而且能求出比拟合法更可信的活化能的值。
3.5 线性增量等转化率微分法
Budrugeac46提出一种简单而精确的增量等转化率微分法,可以适用于任意温度程序下的记录的动力学数据。他认为在一个很小的转化率变化范围内,活化能和指前因子都是不变的,即dα/dt ≈Δα/Δt。T和f(α)的平均值分别为:。
这样方程dα/dt=Af(α)exp(−E/RT)

以lnΔtα对作图,可以得到任一转化率下的Eα和的数值。
在不同升温速率扫描条件下,该方程(20)可以写为:

其中,ΔTα = Tα−Tα−Δα
以lnβ/ΔTα对作图,可以得到任一转化率α和Δα下的Eα和的数值。
该法与Ortega法39的不同之处在于避开了温度积分近似式,并且用代替,可以得到更为精确的动力学计算结果。
3.6 改进的Madhusudanan-Krishnan-Ninan法
Madhusudanan-Krishnan-Ninan (MKN)法是对单一扫描速率下测得的TA数据进行动力学分析的方法,通过代入各种动力学模式函数而获得动力学参数的方法,也称作“模式配合法”。张建军等人47对此方程(22)进行改进后,将其变为多重扫描速率法,在不涉及动力学模式函数的前提下,获得较为可靠的活化能值,也叫无模式函数法。

改进的MKN方程如下:
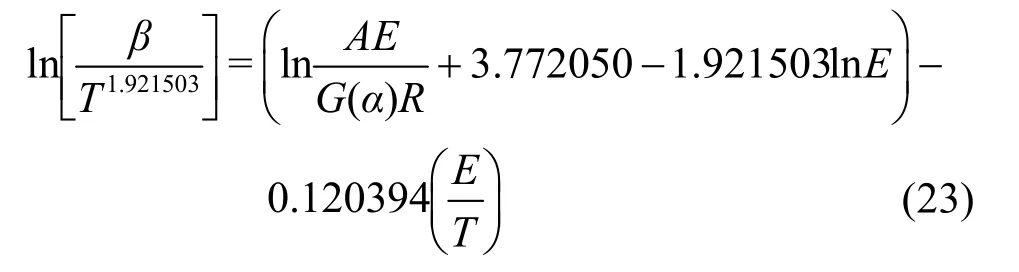
3.7 改进的双等双步法
张建军和任宁等27在转化率法和变异的等转化率法的基础上提出了一种新的热分析动力学数据处理方法,即双等双步法。该法的优点是机理函数和活化能分别求取。为了能得到更精确的活化能数值,张建军等人48通过引入Ozawa迭代方程49对此方法进行了改进,具体步骤如下:
(1) 确定机理函数
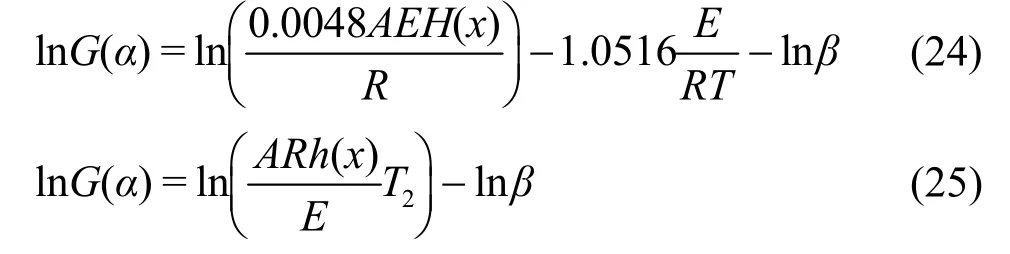
代入同一温度下的α、G(α)、β的数值,以lnG(α)对lnβ用最小二乘法进行线性回归,得到不同温度下的直线的相关系数、斜率和截距。其中线性关系较好且斜率接近于−1者所对应的机理函数,即为该反应最可几的机理函数。
(2)E和A的求取

代入同一转化率下的温度T、G(α)和β的数值,以ln(β/H)对1/T或者ln(β/hT2)对1/T作图,用线性最小二乘法从斜率得初值E,采用迭代法计算活化能的值,直到满足∣Ei−Ei−1∣< 0.1 kJ·mol−1,即可得到较为合理的E值。
4 总结和展望
2018年,Vyazovkin在《热分析和量热法手册》31提到“过去十年来,等转化率方法取得的重要进展与可变活化能的定量解释有关。”这将有助于更好的理解和更有效地使用各种等转化率方法。目前,不等温等转化率方法在处理热分析动力学数据方面有明显的优势。但是研究者们更习惯采用比较传统的等转化率方法,而近年来提出的新型等转化率法使用却较少。另一个不容忽略的问题是该法基本沿用了等温、均相体系的动力学理论和方程,并且是基于不同TA曲线下,同一转化率处的活化能是常数的这一基本假设而提出的,因而忽略了非均相反应体系的复杂性、样品的热效应、颗粒几何形状、堆积方式以及温度积分使用不当等因素,会导致动力学分析的误差。同时研究者们发现如果因为实验操作者不同、仪器不同而导致实验结果重复性差,则会影响热分析动力学的最终计算结果。
Vyazovkin在综述30里提到必须有充足的、合适的热分析动力学数据,才能得到更合理的动力学计算结果。因此建立统一的热分解动力学研究标准,规范热分析动力学实验操作,对推动热分析动力学的进一步研究与发展具有非常重要的意义。
长期以来,国内外学者在热分析动力学理论完善和研究标准方面已经做出了大量的工作,如修正动力学方程、改变实验条件、归纳影响因素、提出多种热分解动力学模式函数和数据处理方法以及适用于多步热分解步骤的多元非线性拟合法50等。
因此,探索在实验的基础上修正Arrhenius公式或者改变速率常数与温度的关系式,提出更适合于非等温、非均相的速率方程,深入研究多步骤固相反应机理,建立统一的热分解动力学研究标准,是热分析动力学研究迫在眉睫的重要工作。ICTAC重点强调需要广泛地使用更精确的热分析动力学研究方法。只有通过互补才能提高分析结果的可靠性1。当然,还需要进一步努力推广现代的等转化率积分法和微分法。
可见,热分析动力学理论的完善将需要热分析研究者投入大量的精力,付出长期和执着的劳动。我们相信在不久的将来,热分析动力学理论、方法和应用将会日趋完善和成熟。