导流锥锥型对燃气弹射内弹道的影响数值研究

赵 谢，程洪杰，赵 媛，高 蕾

(火箭军工程大学 兵器发射理论与技术军队重点学科实验室，西安 710025)

0 引言

燃气弹射作为一种新型的冷发射技术，具有结构简单、出筒速度高、导弹射程远等优点，采用燃气发生器作为动力源将导弹弹射出发射筒，燃气在喷管内加速膨胀形成射流，经导流锥分流后进入初容室内，所以导流锥的结构参数会直接影响燃气射流的冲击角度和运动轨迹，对流场结构影响较大。

自McKinnis等[1]提出燃气弹射概念以来，对燃气弹射的研究方法大都采用半理论半实验的方法进行研究。于勇等[2]研究了同心筒导弹弹底受到附加弹射力的作用，其值主要取决于排气狭缝宽度、导流锥等因素，并利用数值模拟技术进行验证，得到了增加导流锥能降低筒底所受的冲击力的结论；刘念昆[3]分析了车载导弹垂直发射系统的超音速射流流场结构，建立了燃气排导模型，得出合理增加导流锥的折转半径和冲击高度都可有效降低燃气流场产生的危害；唐洪等[4]研究了在同心筒垂直发射装置发射过程中导弹周围高温燃气环境对导弹的影响，采用了数值仿真方法对两种导流方式进行了计算模拟比对，导流锥型同心筒明显地减小了发射筒底的压力和温度。针对减小发射筒底部压力和温度的问题，苗佩云等[5]通过运用数值模拟的方法研究了导流锥对于冲击力的影响，得出了增加导流锥能降低冲击力的结论，但是对于导流锥结构参数没有进行具体的设定；姜毅等[6]采用了数值仿真的方法对于同心筒导流锥的尾部收缩段的尺寸进行了改变，结果表明改进方法能够有效改善导弹发射过程中的热环境。但是以上研究没有对导流锥锥型进行详细的设计与分析。

本文以燃气弹射装置为物理模型，采用有限速率/涡耗散模型和RNGk-ε湍流模型建立了二维轴对称网格模型，运用动网格技术，对导流锥锥型进行改变，并对比研究直线锥、抛物线锥、双曲线锥和椭圆锥等锥型对弹射内弹道的性能影响，为弹射装置的内弹道优化提供理论支撑。

1 物理模型和数值计算

1.1 物理模型和基本假设

燃气弹射装置主要由燃气发生器、导流锥、发射筒、喷管、尾罩、底座及支撑结构组成。其中，喷管采用拉瓦尔喷管，导流锥采用的是圆锥型面，底座采用自适应橡胶底座，尾罩采用下凹式。通过导流架结构将燃气发生器与导流锥进行连接[7]，并利用细长的支撑结构固定于筒底，因支撑结构细长对流场影响较小，几何模型简化后如图1所示。其中，P点为实验和数值仿真的监测点。弹射的物理过程为：低温推进剂在燃气发生器中燃烧经喷管加速喷出，通过导流锥改变燃气射流方向，在发射筒内迅速建压，推动导弹向上运动。

基本假设：

(1)燃气发生器喷出的燃气射流中无固体颗粒；

(2)低温弹射流场内气体均为理想气体，满足理想气体状态方程；

(3)忽略燃气辐射和重力影响；

(4)忽略燃气发生器与初容室的传热交换。

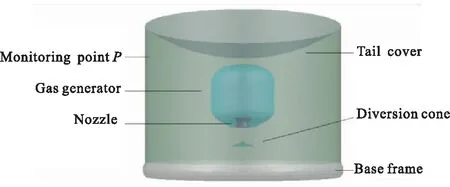
图1 燃气弹射装置几何模型

1.2 仿真计算方法

由于数值模型具有高度轴对称特性，采用有限体积法[8]进行数值离散时，结构化网格比非结构化网格质量更高，更能够保证网格计算的准确性和可靠性，更加容易收敛，故网格模型采用二维轴对称式结构，如图2所示。

喷管采取压力入口，总压曲线如图3所示，各喷管入口组分质量分数如表1所示。

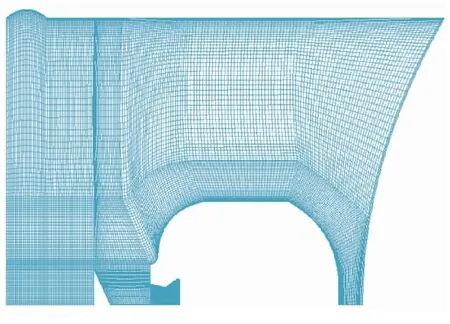
图2 网格模型

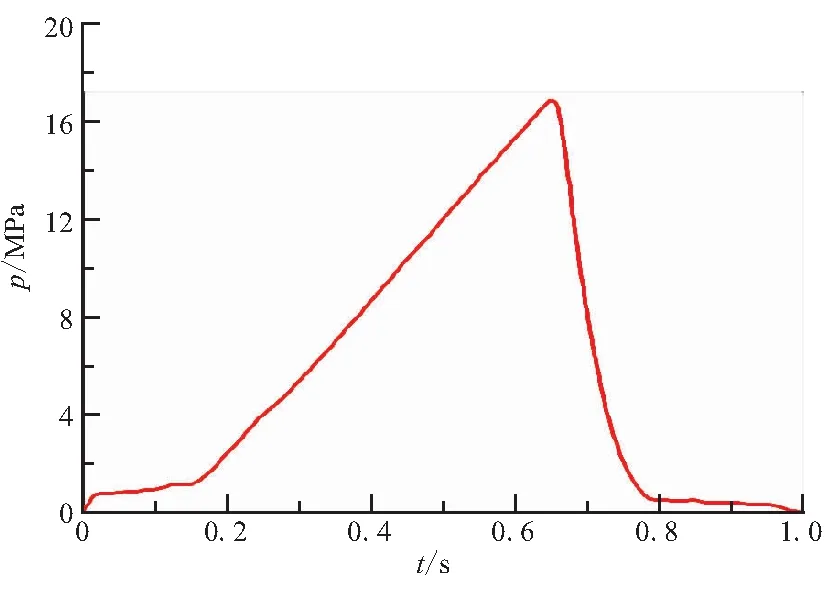
图3 喷管入口总压曲线

表1 喷管入口组分及质量分数

2 网格无关性检验

对于包含多组分燃烧的非定常工程问题，数值计算的精度对网格大小和质量有较强的依赖性，因此有必要进行网格无关性检验。为检验无关性，采用三种网格密度工况下的流动模型进行数值计算，工况1、工况2和工况3分别为2.2万网格、6.0万网格、10.0万网格。提取三种网格数量下P点的压力及温度载荷作为比较对象，如图4所示；抽取0.1t0时刻和0.5t0时刻进行相对偏差计算，如表2所示。其中，p0为监测点的参考压力值，T0为监测点的参考温度值，t0为推进剂燃烧完全所用时间。

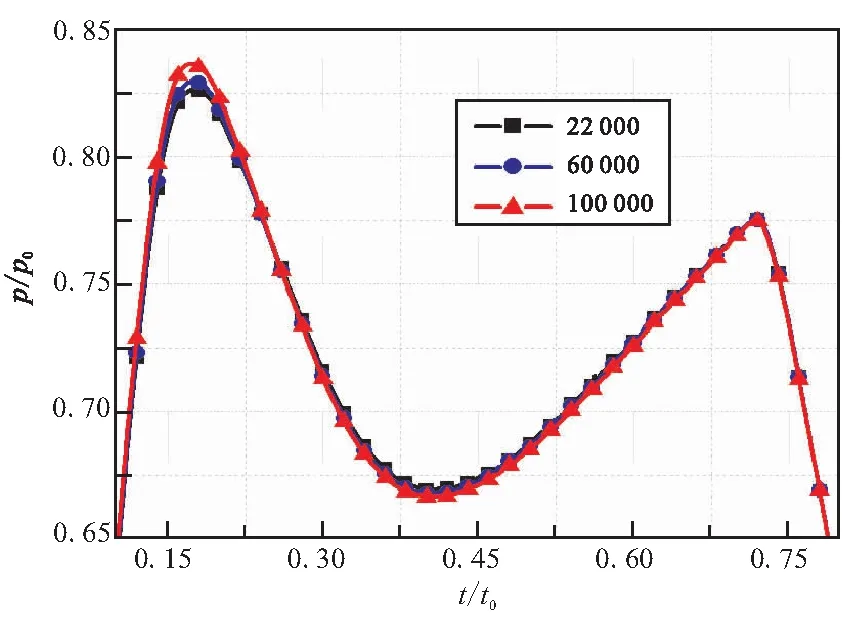
(a)Pressure comparison of the point P

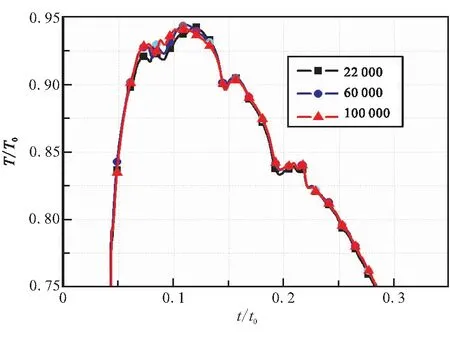
(b)Temperature comparison of the point P

表2 两个时刻抽取结果

由图4和表2可见，三种网格数量下P点压力曲线和温度曲线具有相同的趋势，且相对误差不超过1%。考虑到计算效率的需要，选择2.2万网格分析燃气弹射内弹道的流场和载荷特性。

3 数值方法验证

为验证数值方法的准确性，采用前文确定的数值计算模型，将P点的计算值与实验值进行对比，实验值参考文献[9]，如图5所示。可见，压力与温度的数值曲线与实验曲线吻合度较高，趋势大体一致，成功捕获压力曲线的双峰值以及温度曲线的单峰值。实验得到的第一个压力峰值为0.83p0，二次压力峰值为0.79p0，相应的计算值也为0.83p0和0.79p0，但较实验值稍有延迟。实验测得的温度峰值为0.95T0，计算值为0.92T0，数值计算结果与实验值最大误差为3.1%，计算精度满足工程需要，表明所建立的数值模型和计算方法具有较高的可信度，可用来作为基础模型进行优化。

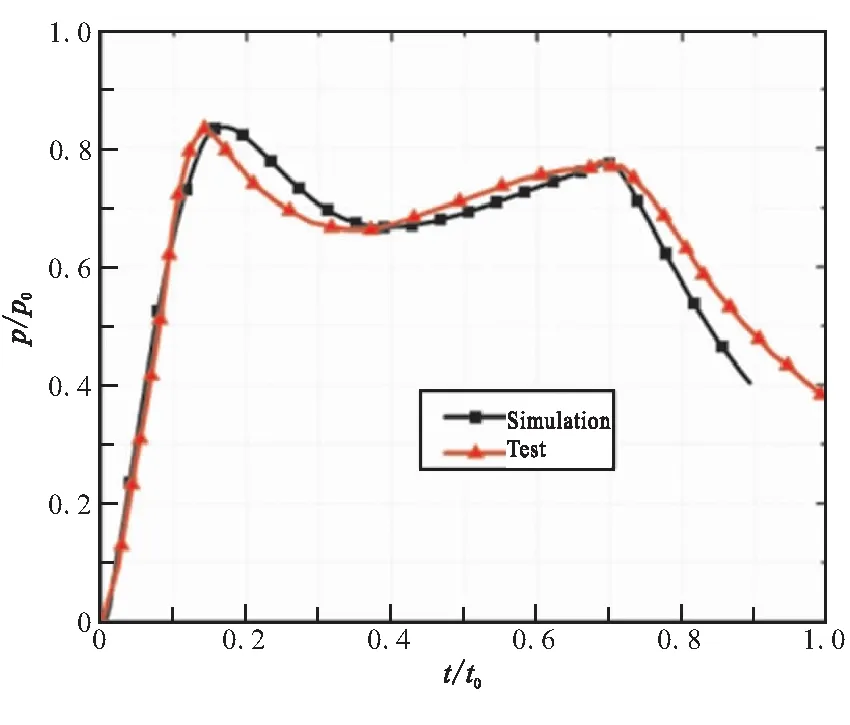
(a)Pressure curves

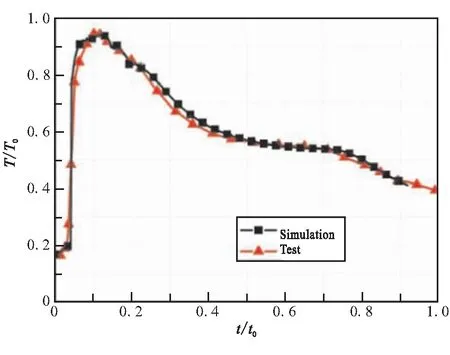
(b)Temperature curves

4 导流锥锥型对弹射流场与载荷特性的影响

导流锥的主要作用是改变喷出的燃气流的流动方向，当高温高速的燃气流遇到导流锥时，燃气的流动受到了阻碍，同时导流锥也受到了燃气的冲击力，如果燃气与导流锥的接触面为平面，则气流对接触面的作用力最大，此时燃气的总能量将全部转化为压强作用在挡板上；如果说接触面为曲面，燃气会部分被反射，此时只有部分能量转化为压强作用在挡板上，燃气流对接触面的作用力将减小[10]。

为研究导流锥锥型对弹射流场的影响，现选取导流锥母线为直线、抛物线、双曲线及椭圆线的导流锥结构形式进行分析。在本文中，将其分别称为直线锥、抛物线锥、双曲线锥、椭圆锥。

4.1 流场分析

由图6可见，曲面锥锥型对于流场结构的影响较大，燃气射流经导流锥整流后，形成了顺时针的大涡和逆时针的小涡。在0.1t0时刻，当导流锥锥型由平面变为曲面，导流锥下方形成的漩涡面积更大，在锥型为椭圆锥时，导流锥下方的涡数由1个变为2个，并且由1个逆时针小涡变为2个方向不同的小涡，涡的形状也在发生变化；不同的锥型设计，导致燃气反射点在筒底的位置也在发生改变，这是由于导流锥母线的线型弧度不同而造成的。

结合对图6的流场分析，由图7、图8和图9可见，导流锥锥型的改变对于氧气的空间分布有较大的影响。当锥型为直线锥时，由于导流锥母线为直线，燃气沿着锥型线直接到达反射点，随即贴着发射筒壁面进行燃烧反应，而锥型母线为曲线时，燃气反射点外移，反射轨迹弧线变短。当锥型为抛物线锥时，燃气未得到充分的整流，在进入发射筒内，筒内的氧气消耗速率明显慢于直线锥和双曲线锥，二次燃烧区域部分转移至筒底。当锥型为椭圆锥时，二次燃烧区域已蔓延至发射筒壁，筒底的氧气最早被消耗，由于漩涡增多而造成的“卷吸”作用增大，这与流线图和氧气质量分数变化曲线图所展现的过程吻合，在0.1t0～0.2t0时段，抛物线锥与椭圆锥的氧气消耗速率快于直线锥，随后在0.3t0时刻，各锥型氧气耗尽。由于锥型母线弧度原因，抛物线锥与椭圆锥的喷管处的氧气剩余量较直线锥与双曲线锥要高。

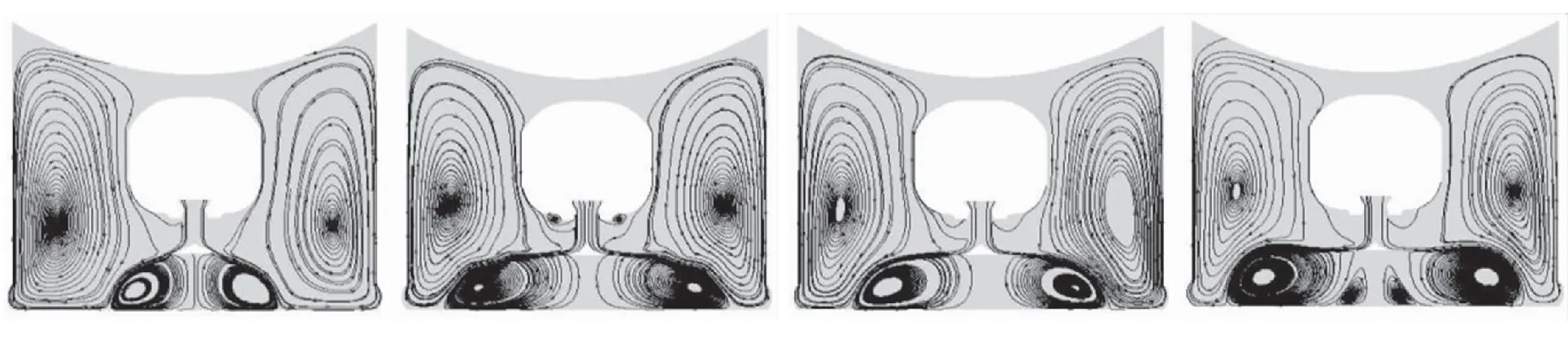
(a)Line cone (b)Parabola cone (c)Hyperbola cone (d)Ellipse cone

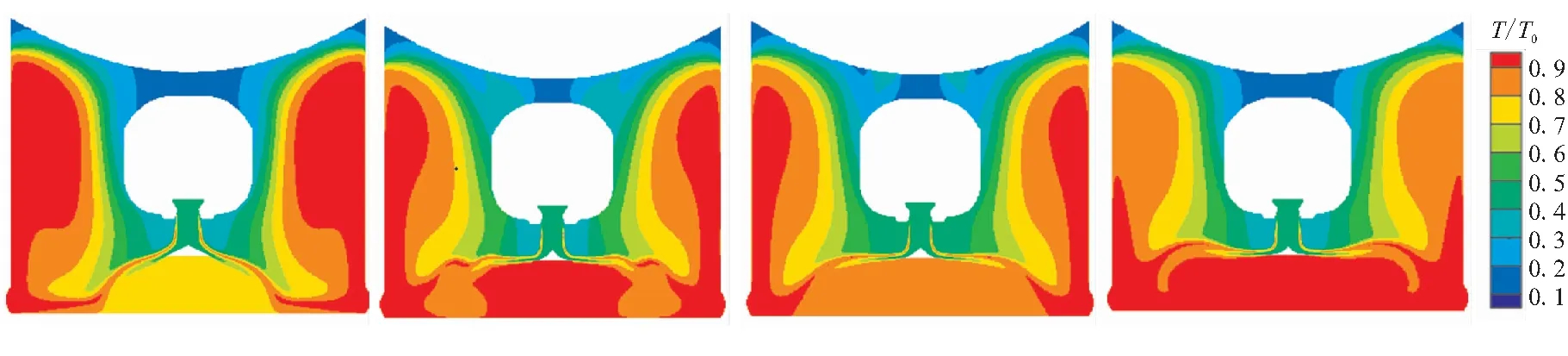
(a)Line cone (b)Parabola cone (c)Hyperbola cone (d)Ellipse cone

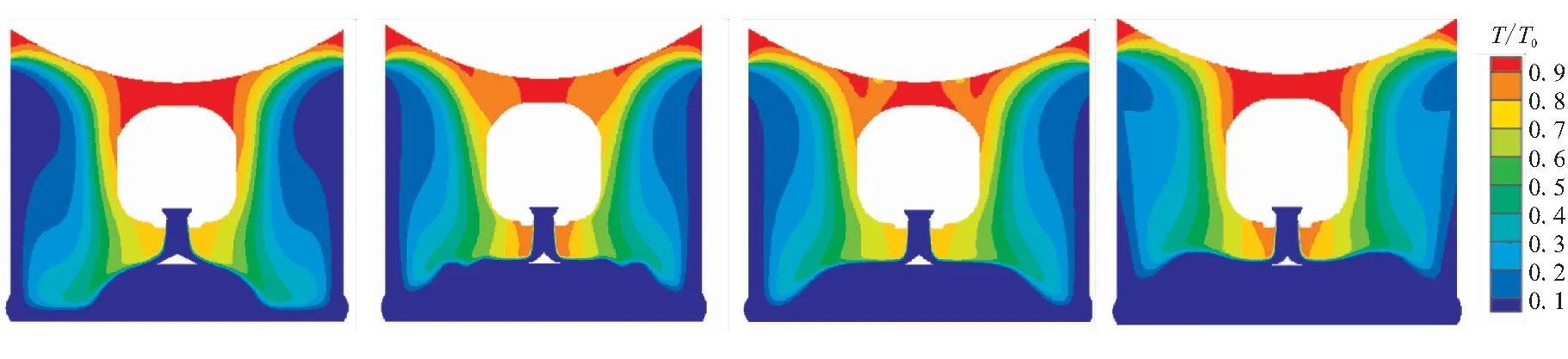
(a)Line cone (b)Parabola cone (c)Hyperbola cone (d)Ellipse cone

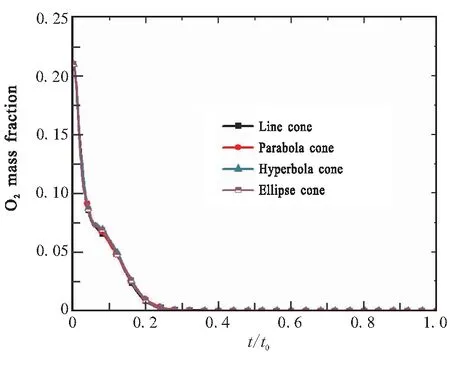
图9 氧气质量分数随时间变化曲线

4.2 载荷分析

图10和图11的(a)、(b)分别为监测点P的压力和温度曲线对比及发射筒底的平均压力和平均温度对比。

由图10(a)可见，锥型的改变对于监测点P的压力不会有太大的影响，曲线走势基本一致，这说明导流锥型对于燃气的引导作用主要体现在发射筒的下方区域。由放大图可见，直线锥压力峰值最大，椭圆锥最小，压力的初始峰值是由于二次燃烧导致筒内压强急剧上升，二次峰值与总压曲线峰值时刻保持一致，这是由于燃气的不断输入所造成的。由图10(b)可见，抛物线锥、双曲线锥、椭圆锥的温度峰值较直线锥偏小，出现了时间上的滞后，这是由于在0～0.3t0时段，二次燃烧区域聚集在导流锥下方，还未延伸至检测点P点处。在0.24t0时刻，椭圆锥温度骤降，随即回位。在0.3t0时刻以后，四种锥型的温度曲线走势基本一致。

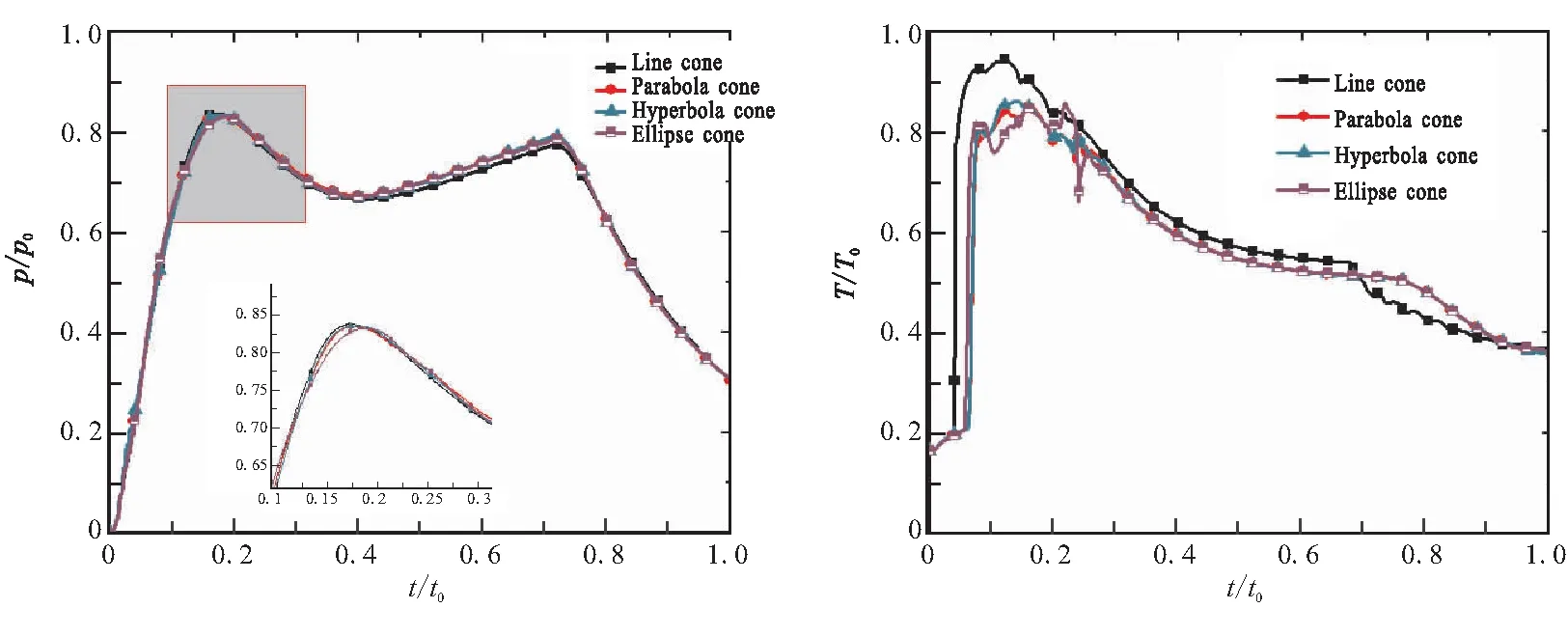
(a)Comparison of pressure curves (b)Comparison of temperature curves

(a)Comparison of pressure curves (b)Comparison of temperature curves

由图11(a)可见，三种曲线锥筒底压力不会出现初始峰值，而是一直处于上升状态，在0～0.2t0时段，四种锥型压力曲线走势和峰值基本一致，在0.2t0时刻以后，三种曲线锥筒底压力明显高于直线锥，其中椭圆锥和抛物线锥高于双曲线锥。由于二次燃烧区域聚集于导流锥下方，因而筒底压力载荷会相应增加，曲线走势和峰值出现时刻与总压曲线相一致，约在0.72t0时刻。曲线锥对于筒底无二次压力冲击，压力峰值的高低与锥型母线的弧度有关，弧度越小，燃气射流更容易冲击筒底，导致筒底压力最大。

由图11(b)可见，在0～0.24t0时段，二次燃烧剧烈，导致曲线锥温度高于直线锥，但0.24t0时刻以后，二次燃烧燃气中的可燃成分H2和CO剧烈的放热反应结束，缺氧无反应阶段开启，曲线锥筒底温度低于直线锥，这是当筒内氧气耗尽后，筒底温度开始下降，随着单位时间喷管入口燃气量增加，导流锥锥型母线的弧度直接影响燃气向上走，筒底温度减小。

4.3 内弹道特性分析

图12分别为各导流锥锥型的导弹加速度、速度和位移随着时间变化曲线对比。四种锥型内弹道数据对比如表3所示。

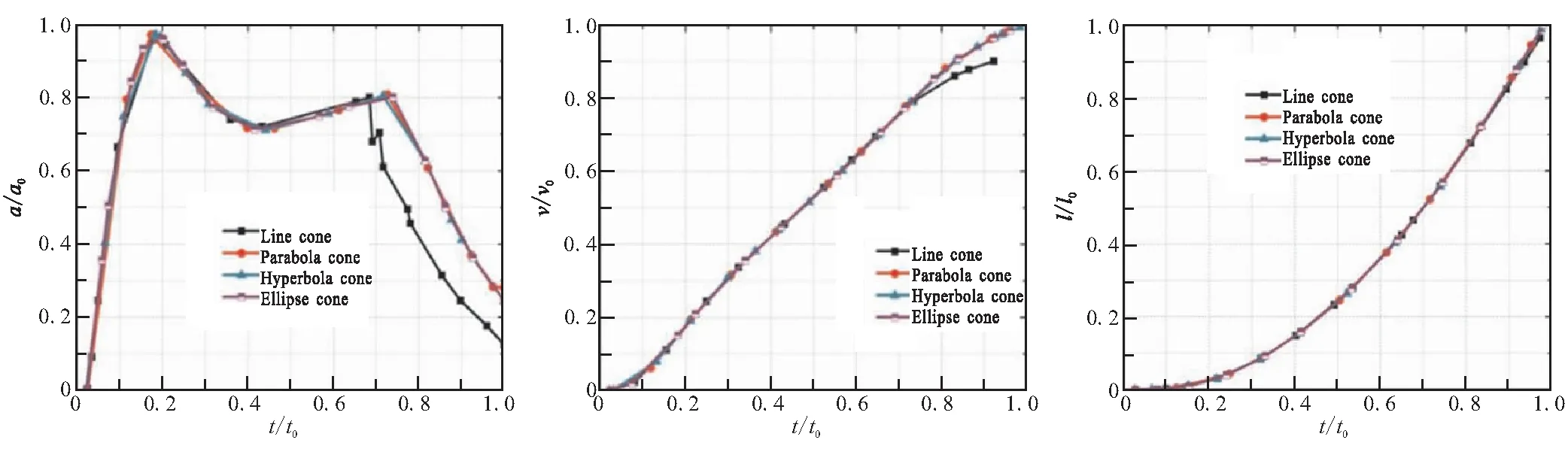
(a)Acceleration (b)Velocity (c)Displacement

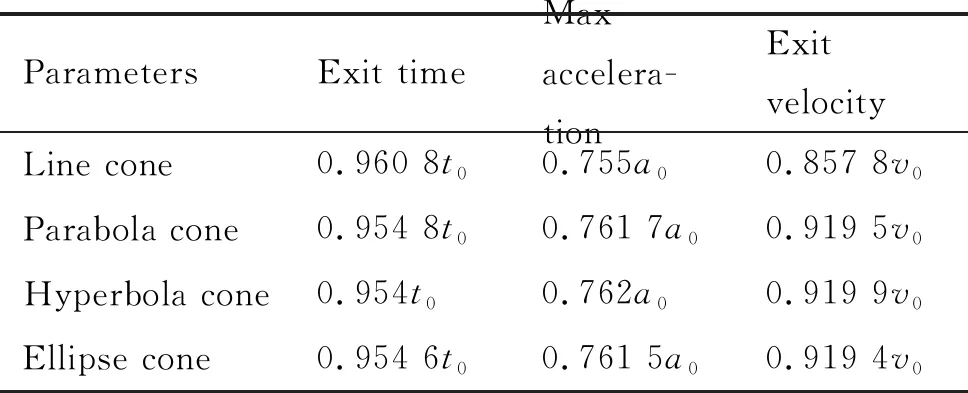
表3 四种锥型内弹道数据对比

由图12及表3可知，改变导流锥锥型后，曲线锥导弹的加速度较直线锥相对平稳，位移曲线走势相对一致。根据导弹设计要求，出筒速度范围为0.8v0～0.95v0，导弹筒内加速度不大于0.98a0[11]，可知，各个锥型皆满足内弹道设计要求，与直线锥相比，抛物线锥的出筒时间延迟了0.62%，加速度峰值增加了0.89%，出筒速度增加了7.21%；双曲线锥的出筒时间延迟了0.7%，加速度峰值增加了0.93%，出筒速度增加了7.26%；椭圆锥出筒时间延迟了0.65%，加速度峰值增加了0.86%，出筒速度增加了7.23%。双曲线锥在二次燃烧过程中无脉动现象，筒内温度较低，因此导流锥型为双曲线锥时的发射筒结构是最优结构设计。

5 结论

本文建立了考虑二次燃烧燃气弹射内弹道数值模型，采用了RNGk-ε、有限速率/涡耗散模型以及动网格技术，研究了导流锥锥型对燃气弹射初容室内的流场特性的影响，得到以下结论：

(1)分析了四种不同锥型的导流锥对于流场结构以及氧气消耗速率的影响。结果表明，锥型的改变主要对于发射筒内部的二次燃烧区域的范围产生影响。曲面锥下方形成较大回流区，二次燃烧高温区域转移至筒底区域，锥底温度升高，氧气消耗率增大，椭圆锥最为明显；抛物线锥在进入发射筒内加速膨胀时出现脉动，筒内氧气消耗速率明显快于直线锥和双曲线锥。

(2)分析了四种不同锥型的导流锥对于筒底的载荷作用。结果显示，直线锥存在二次压力冲击现象，曲线锥筒底压力曲线呈现先增大后减小的变化趋势，对于筒底压力无二次冲击，椭圆锥筒底压力峰值最高，双曲线锥最低，这与导流锥锥型母线的弧度有关，弧度越小，燃气射流更容易冲击筒底，导致筒底压力最大。

(3)分析了四种不同锥型的导流锥对于初容室内流场和内弹道变化规律。结果显示，曲线锥筒壁温度比直线锥要低，抛物线锥与双曲线锥的温度走势大致相同，椭圆锥在0.24t0时刻出现轻微震荡，这是因为曲线锥二次燃烧区域主要聚集于锥底，发射筒与燃气发生器间的高温区域变小，有效地减小了发射筒壁面温度，增加了导弹出筒速度，缩短了出筒时间，双曲线锥对比直线锥出筒时间缩短了0.7%，加速度峰值增加了0.93%，出筒速度增加了7.26%。