配置点谱方法-人工压缩法(SCM-ACM)求解同心圆筒内流体流动
刘宇浩,周家秀,王露宁,崔 苗,林 欢,张敬奎*
(1.山东省余热利用及节能装备技术重点实验室 青岛理工大学,青岛 266033;2.工业装备结构分析国家重点实验室 大连理工大学,大连 116024)
1 引 言
工程领域中存在着大量圆筒内不可压缩流体流动问题,对该类问题的研究分为解析方法、实验方法和数值模拟法。数值模拟法作为研究和分析不可压缩流动问题的方法之一,随着计算机技术的发展已然成为不可或缺的研究手段。
谱方法是一种高精度的数值方法,计算量大的特点使其发展受到很大程度的限制。直至快速傅里叶变换的出现,谱方法才得以大量采用。如Yokota等[1]分别选取Lagrangian涡旋法和谱方法模拟了衰减均匀各向同性的湍流,对比发现谱方法计算速度比Lagrangian涡旋法快一个数量级。Khater等[2]选取基于切比雪夫多项式的配置点谱方法求解了Burgers型方程组,与其他先前的方法相比,谱方法提供了更好的准确性。Li等[3]成功地发展了圆柱和矩形三维坐标系中辐射流体力学和辐射磁流体力学的配置点谱方法,研究了热辐射及磁场对流体流动和传热的影响。由于谱方法具有以上的优势,使其大量应用到传热学、计算流体力学和磁流体力学等领域[4-12]。
人工压缩法由Chorin[13]提出,是一种简单且准确的算法,其核心是在连续性方程中引入与人工压缩项相关的伪时间项,在稳态不可压缩N-S方程中引入伪时间项,即∂/∂t。将粘性稳态不可压缩流动转化成虚拟的粘性非稳态可压缩流动,当时间t→∞时,∂/∂t→0,这样粘性非稳态可压缩流动就会逼近粘性稳态不可压缩流动。目前,该方法已广泛用于求解弱可压缩和不可压缩流动问题[14-18],可以看出,人工压缩法具有形式简单、易于实施和收敛的特点。
由于配置点谱方法和人工压缩法两种方法所具有的以上优势,将两种方法结合起来发展了SCM-ACM用于求解同心圆筒内的不可压缩流体流动问题。张敬奎等[19]已经在直角坐标系下将两种方法相结合,成功计算了不可压缩流动和传热问题,且在计算精度和效率上也取得了非常理想的效果。本文将在前期已完成的直角坐标系统下SCM-ACM开发的基础上,推广到柱坐标系统,拓展该数值方法对不同几何模型中流动问题求解的适用性。
2 人工压缩格式非稳态控制方程
本文发展了数值方法SCM-ACM用于求解柱坐标系统下的不可压缩流体流动问题,并选取同心圆筒间旋转流动Taylor-Couette流作为测试对象。具体几何参数的定义和几何模型如图1所示,人工压缩格式的无量纲控制方程为
(1)
(2)
(3)
(4)
式中参数c为人工压缩因子,r为半径方向,θ为周向方向,z为高度方向,t为时间,U,V和W分别为圆柱体径向、周向和轴向上的无量纲速度,P为无量纲压力,Re为雷诺数。
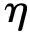

图1 同心圆筒间旋转流动的几何模型
Fig.1 Geometric model of rotational flow between concentric cylinders
3 数值方法
3.1 空间离散
选取配置点谱方法离散空间偏微分项,离散过程包括配置点的选取、计算区域的转换以及系数的确定。
3.1.1 配置点的选取
在r和z方向均采用 Chebyshev-Gauss-Lobatto配置点,在θ方向,采用 Fourier-Gauss-Lobatto配置点。
Chebyshev-Gauss-Lobatto配置点:
xi=cos(πi/N) (i=0,…,N)
(5)
Fourier-Gauss-Lobatto配置点:
θj=2πj/Nθ(j=0,…,Nθ-1)
(6)
根据三个方向的配置点计算公式,可将选取的同心圆筒间旋转流动的几何模型划分为如图2所示的网格系统。可以看出,网格在径向边界处分布密集而中间比较稀疏,该类型的网格系统适用于速度梯度较大的边界条件,能够满足较高计算精度的需要,体现了该网格的优良特性,为之后求解圆筒内的不可压缩流体流动问题提供了保障。
3.1.2 计算区域的转换
谱方法离散方程时,Chebyshev配置点谱方法规定计算区域在[-1,1]之间的谱空间内,Fourier配置点谱方法规定计算区域在[0,2π)之间的谱空间内,本文只需要对r和z方向计算区域进行转换即可。计算区域转换的步骤如下。
(7)

图2 同心圆筒间旋转流动的网格系统
Fig.2 Grid system of rotational flow between concentric cylinders

(8)
(9)
3.1.3 系数的确定
在使用谱方法时,把控制方程的未知函数用级数形式表示。

(10)
式中T(ξ)为Chebyshev多项式。以Chebyshev-Gauss-Lobatto配置点为例,ξ=cos(πj/N)(j=0,1,…,N)。

(11)
矩阵形式为
(12)

3.2 时间离散
将代数方程采用显式差分格式进行求解,对流项采用Adams-Bashforth格式,具体离散形式为
(13)
(14)
式中Δt为时间步长,U为速度矢量。对离散后矩阵形式的方程给定初值和边界条件即可求解出速度分布。
4 结果分析
本文选取同心圆筒间旋转流动Taylor-Couette流作为计算对象,其在很多领域均有应用,这种流动随雷诺数的增大表现出了一些典型的非线性动力学行为,因此对其研究有重要的理论意义。为检验本文发展的SCM-ACM计算代码,选取参考文献[20-22]的三个Taylor-Couette流算例作为验证依据。三个参考文献所采用的Taylor-Couette流的几何条件和边界条件分别为
几何条件:

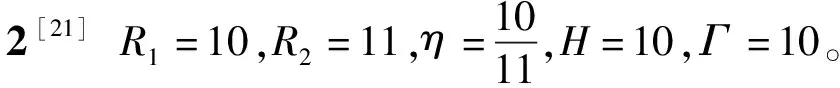

边界条件:
三个算例均为相同的边界条件:
R=R1处,U=0,V=1,W=0
R=R2处,U=0,V=0,W=0
Z=Z1处,U=0,V=0,W=0
Z=Z2处,U=0,V=0,W=0
4.1 网格独立性检验
针对Taylor-Couette流,首先进行了网格独立性检验。根据其几何特点,设定径向和周向节点数相同,高度方向节点数根据尺寸设置较多。选取圆筒间半径r方向的平均速度作为网格独立性测试的变量,当雷诺数等于100时,r方向平均速度随网格节点数变化如图3所示,其中r,θ和z三个方向的节点分别选取为15×15×31至31×31×61。
可以看出,当选取较少的网格节点数时,平均速度的变化较大;当节点数超过21×21×51后,平均速度的变化不明显,此时网格节点数再增加已对计算结果的影响较小,达到网格独立解。但同时,选取的点数越多,达到同样计算次数需要的计算时间也随之显著增长,列入表1,因此本文选取25×25×51的节点数。

图3 Re=100时r方向平均速度随网格节点数的变化
Fig.3 Average speed in therdirection changes with the number of grid nodes with Re=100
4.2 程序有效性验证
针对参考文献[20-22]的Taylor-Couette流算例,本文采用SCM-ACM所计算的结果与文献的结果对比,如图4~图6所示。其中图4是文献[20]的算例,分别为Re=100,Re=120,Re=130,Re=135,Re=140和Re=150时所绘制的r-z截面速度矢量。图5是文献[21]的算例,为Re=300时的Taylor涡流线。图6是文献[22]的算例,为Re=50和Re=100时的r-z截面速度矢量、周向速度等高线和压力等高线。
从图4的r-z截面速度矢量的分布可以看出,Taylor涡的数量、分布位置以及流向几乎一致,本文发展的SCM-ACM计算结果与文献[20]的计算结果吻合很好。在图5中,本文把Re数增加到300,结果与文献[21]的结果吻合较好,旋涡数目和结构一致。图6中Re=50和Re=100时,本文r-z截面速度矢量、周向速度V等高线和压力P等高线与文献[22]的结果在整体上吻合很好,但细微处略有差异,这种差异可能源自数值离散方法的差异。因为,同样采用谱方法离散控制方程的本文结果和文献[20]的结果吻合度更好。通过以上三个算例的对比,说明本文发展的配置点谱方法与人工压缩法相结合的SCM-ACM数值方法是有效的,能够用于求解圆筒内的不可压缩流体流动。
表1 不同网格节点数计算需要的时间
Tab.1 Calculating time under different nodes

节点数目15×15×3117×17×4121×21×5125×25×5127×27×6131×31×61时间/s53881016119466241872759428184

图4 从左到右分别为Re=100,Re=120,Re=130,Re=135,
Re=140和Re=150的r-z截面速度矢量
Fig.4 Velocity vector inr-zsection,from the left to right
Re=100,Re=120,Re=130,Re=135,Re=140 and Re=150 respectively

图5 Re=300时r-z截面Taylor涡流线
Fig.5 Taylor vortex distribution inr-zsection with Re=300

图6 Re=50和Re=100时的r-z截面速度矢量(左)、
速度V分布(中)和压力P分布(右)
Fig.6 Velocity vector ofr-zsection(left),velocityVdistribution
(middle)and pressurePdistribution(right)at Re=50 and Re=100
4.3 SCM-ACM的收敛特性
选取文献[22]算例,绘制了Re=50时残差随迭代次数的变化趋势和残差随网格节点数的变化趋势。本文设置的收敛残差是指下一时层所有节点速度和压力与当前时层所有节点速度和压力的最大差值,即ε(u)=max.(un + 1-un)。可以看出,计算残差随计算次数指数下降(纵坐标为以10为底的对数坐标),同样随计算节点的增加而指数下降。


图7 速度分量U,V,W和压力P的残差随迭代次数和网格节点数的变化
Fig.7 Residual error ofU,V,WandPwith the number of iterations and the number of nodes
5 结 论
本文发展了柱坐标系下SCM-ACM的数值方法,并选取同心圆筒间旋转流动Taylor-Couette流这一典型流动问题为测试对象,检验了SCM-ACM求解圆筒间粘性不可压缩流动问题的网格独立性和程序有效性,并分析了SCM-ACM的收敛特性。结果显示,本文发展的柱坐标系下SCM-ACM数值方法能够与多个参考文献的计算结果很好吻合,适用于求解柱坐标系下稳态不可压缩流动问题,且具有指数收敛的特性,为求解柱坐标下粘性不可压缩流动问题提供了一种新的数值选择。

