基于最小二乘的工程结构边界载荷反求误差消减方法
李玉良,何宇轩,楚 盖,韩亮亮,陈 萌
(1.东华大学 机械工程学院,上海 201620;2.中国航发沈阳发动机设计所,沈阳 110015;3.上海宇航系统工程研究所,上海 201108)
1 引 言
疲劳断裂作为机械结构最主要的破坏形式[1],一直都用于预测产品的寿命[2,3]。鉴于生产过程中对裂纹处的应力和应变进行直接测量非常困难,对工作结构加上边界载荷进行疲劳寿命计算是可行的方法,而获得结构的实际边界载荷是计算的前提。然而,由于土壤和砂石等工作介质的切削及铲运阻力模型难以精确建立,并且装备传动过程中的摩擦等损耗难以精确计算,使得准确获知工程结构的边界载荷非常困难。
目前,工程装备的设计资料中虽然有一些有关工作载荷的经验计算公式[4],可以用来估算装备的动力需求,但这些公式无法给出装备工作过程中的载荷谱,难以对结构进行强度计算并预测其寿命。在边界载荷研究方面,聂影[5]采用多项式函数拟合结构位移曲线,结合奇异函数实现了求解复杂结构等效载荷的目的;李上明[6]建立了无限水域冲击波作用下的结构载荷计算方法;汪谟清等[7]通过台架实验获得了减振器支架某固定点的应变和载荷间的关系矩阵,进而实测应变数据以获得真实载荷;章小龙等[8]针对结构-地基动力相互作用问题,采用黏性边界条件模型模拟地震波作用在地基上的边界载荷;Bae等[9]提出了基于工程数据分析技术的疲劳载荷(应变和应力)提取及传感器最优布局方法;Tessler等[10-12]提出了逆有限元法(Inverse Finite Element Method)用于实时重建全场结构位移;Cerracchio等[13]将精细之字形理论RZT(Refined Zigzag Theory)的运动学假设引入IFEM,用于处理各向异性和非均质材料形成的结构;Song等[14]重构了一般有限元数学模型,识别了施加在实体结构上的接触力,由于该方法使用了大量的求逆运算,因此计算结果的误差较大。上述研究对工作载荷计算都做了有益的探索,但这些载荷计算方法还不能用于基于裂纹扩展的结构疲劳寿命预测问题,对于工作载荷计算过程中的误差还没有给出定量的消减方法。
对于已知结构上某些点的应变反求结构边界载荷的问题,一般可采用解析和数值方法来建立作用于结构的边界载荷和测量应变之间的数学关系。解析法以经典弹性理论为基础,求解过程中一般不需要大量的矩阵运算,计算方便,适用于简单且规则的工程结构。对于复杂的工程结构,很难建立实测应变(应力或位移)与边界载荷之间的数学方程。基于有限元理论,可以将应变、应力或位移与边界载荷通过数学模型联系起来。基于此,本文提出基于测量应变的反求方法来获得结构的边界载荷,该工作属于反问题研究范畴。反问题求解存在三个方面的问题,即解的唯一性、存在性和不稳定性,这也称为反问题的不适定性。反问题解的不稳定性是指尽管数据发生很小的变化,也会使解产生很大的变化,一般称此类问题为病态问题。矩阵条件数是衡量病态矩阵对误差敏感程度的主要参数,Fried[15,16]提出了计算有限元刚度矩阵条件数的方法来判断矩阵的病态性。在计算稳定性方面,正则化方法[10-12,14,17]、变分法[10]或最小二乘法[18]可用来改善计算结果对误差的敏感性,最具代表的Tikhonov正则化方法引入了正则化参数,以降低解的精度[17]为代价来提高稳定性。
本文采用线性矩阵方程理论确定反问题解的存在性和唯一性,采用最小二乘法对计算结果的误差进行分析和消减。结果表明,当输入数据在一定的误差范围内时,反求得到的工作载荷会随着测量应变数量的增加而逐步收敛到真实解。
2 确定等效边界载荷的数学模型
2.1 等效边界载荷
从整体结构中把含有某局部缺陷的结构分离出来,基于局部结构体上的测量应变,采用有限元法确定作用于分离体的等效边界载荷。假定结构体受力F1,F2和F3、转矩T和弯矩M作用,如图1(a)所示,这些外部载荷与图1(b)所示模型等效,该模型有8个未知边界载荷作用(FT 1和FT 2是由扭矩T等效而成,当等效作用点已知时,则含有 1个未知数),这些载荷可以通过8个实测应变来计算。因为一个点上3个方向的应变可以通过一组含有3个应变的应变花测得,所以8个未知等效边界载荷的解至少需要3组应变花。根据圣维南原理,两种不同但静力等效的载荷,在距离加载位置足够远的地方影响会变得非常小。因此,如果加载方式和实测应变的位置满足圣维南原理,则计算结果能较好地匹配实际载荷。
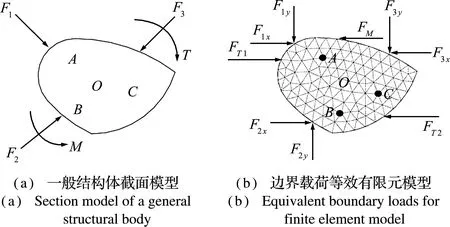
图1 一般结构体截面模型和边界载荷等效有限元模型
Fig.1 Section model of a general structural body,equivalent boundary loads for finite element model
2.2 等效载荷与实测应变的关系式
根据有限元理论,单元的应变与位移关系为
εe=Be·de
(1)
式中εe=[εx,εy,εz,εx y,εy z,εz x]为单元应变矩阵,Be为单元几何矩阵,de为单元所有节点的位移矩阵。
单元刚度矩阵ke可计算为
ke=∭BTDBdxdydz
(2)
式中D为单元弹性矩阵。经过矩阵变换,可以将单元刚度矩阵组合成整体刚度矩阵,即
(3)
式中K为整体刚度矩阵,n为节点数。
因此,有限元的基本方程为
F=K·d
(4)
式中F为节点载荷向量,d为位移向量。
通过在式(4)中加入边界条件,本文只考虑加载条件,F可表示为
F=[0,0,…,0,f1,0,f2,f3,…,fm,0,-fm,0,0]Τ=
Kf·[f1,f2,…,fm]T=Kf·f
(5)
式中f为大小未知的节点等效载荷向量,m为未知载荷的数目,Kf为系数矩阵。
结合式(1,4)可得
(6)
为求解式(6),首先将未知载荷和位移放在方程右边,将已知应变和外部未施加载荷节点移至方程左侧。x为未知变量的向量:
x=[d1,d2,d3,…,dn-1,dn,f1,f2,…,fm]Τ
(7)
式(4)可转化为
[K-Kf]·x=0
(8)
为求解式(8),实测应变数量不应小于独立等效载荷数。因为应变是放置在节点上的,所以节点应变应是其周围节点的平均应变。因此,单元几何矩阵应为该节点周围所有单元节点几何矩阵的平均值,即
(9)
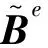
(10)
式中ε1,ε2,…,εm代表测量应变。
根据式(8,10),最终方程为
(11)
一般情况下矩阵A的规模非常大。为了避免计算时间过长,可将矩阵A化简为只含有测量应变和边界载荷的方程,以提高求解效率。化简过程如下。
由式(4,5)可得
K-1·Kf·f=d
(12)
将式(10)代入式(12):
BW·K-1·Kf·f=ε
(13)
因为f和Kf中大部分元素为0,式(13)可化简为
{j∈[1,n]∩n∈[1,m]∩Kfj,p≠0}
(14)
2.3 反问题解的存在性
可用式(11)来解释上述载荷反求方程解的存在性。式(11)中矩阵A为一个(n+m)阶的方阵,n为自由度的数量,m为未知负载的数量。当矩阵A是非奇异矩阵时,式(11)有唯一解。矩阵A可以划分成4个分块矩阵,K是一个n阶非奇异实对称矩阵,Kf可以用K的列向量表示为
Kf=K·Cn × m
(15)
式中Cn × m是一个唯一的系数矩阵。
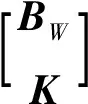
通过改变Kf,可将上述边界条件中的集中载荷变为均匀分布载荷。式(5)体现了这种关系,F=Kf·f,未知数的序列f1,f2,…,fm在F中体现等效加载载荷。
3 误差消减
3.1 误差来源
在有限元的边界载荷计算过程中,会存在多个误差源使载荷偏离真实值,如测量应变的误差与有限元理论近似误差等。可以通过加密有限元网格的方法降低有限元理论近似误差,相关内容可以参考文献[19]。
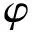


(16)



(17)
3.2 误差减小方法
一般可采用三种方法来减小解的误差。一,找到导致条件数最小的度量位置,这通常需要大量的计算;二,可以采用正则化方法求解病态方程,Tikhonov正则化是最常用也是最著名的正则化方法[20],但是正则化参数的调整难度很大;三,在最小二乘数据拟合问题中,如果所有数据都属于同一个区间且以递增的顺序出现,拟合精度会随着数据量的增多而提高,因此可以使用最小二乘方法获得精确的解[21]。由于在计算过程中所测得的应变比所要求的未知等效载荷的数目多,因此该方法也可以用来减小误差。采用最小二乘法求解过定方程,必须预先确定应变分布区间。

图2 不同网格密度下的位置误差
Fig.2 Location error in meshes with different sizes
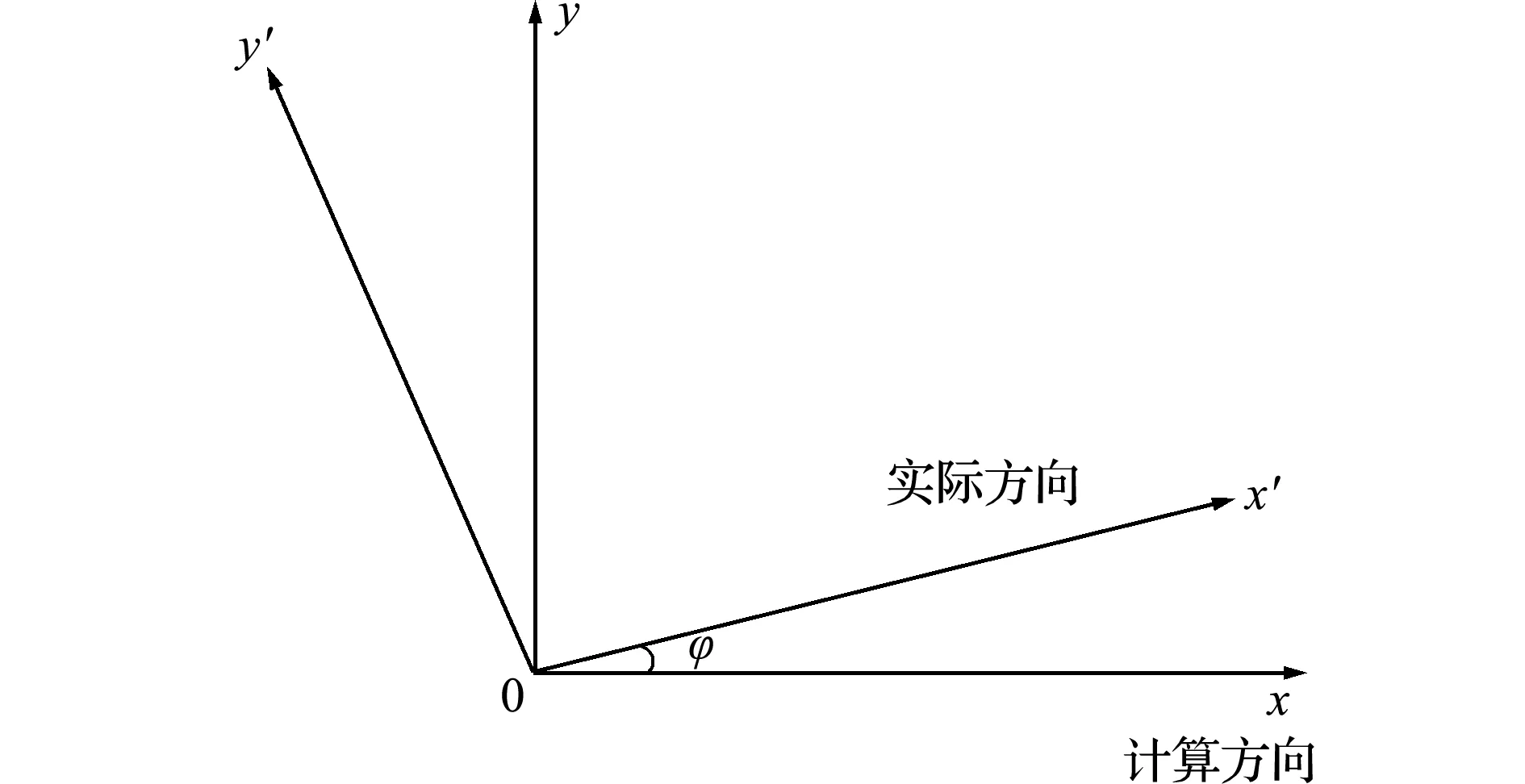
图3 应变角度偏转
Fig.3 Angle deflection of a rosette
根据式(11),矩阵求解误差表示为
(18)
(19)
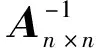
(20)
δb(n + 1)× 1和δbn × 1为测量应变误差。为了比较增加一个应变后的误差,建立表达式为
(21)
式中z表示新增应变的测量误差。
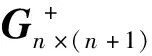
(22)
式(21)的分子可以表示为
(23)
式中mi和ki为常数项。
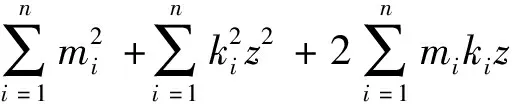
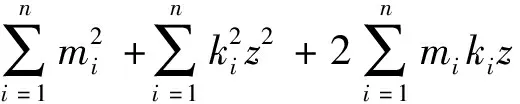
使用过定矩阵的求解方法可以求解z1和z2中的一个,求解方法如下。
因此z1应该为
(24)
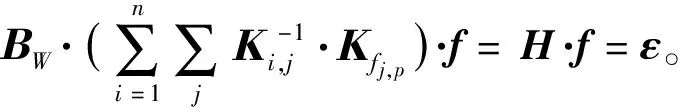
z1=Hp + 1·(Hp × m)+·δεp × 1
(25)
根据式(23),对称轴为
(26)
式中m为等效载荷数目,p为现有应变数目。根据式(26)可得到另一个点,z2=±(|z1-zs|+|zs|),正负号取决于z1和zs的分布。
假设测量应变的误差在真实应变的5%以内,如果多一个应变的误差z属于[z1,z2],则下一个最小二乘解将优于前一个。反复求解式(25,26)可以预测含有更多应变方程的求解结果。
3.3 误差减小方法验证
为验证误差减小方法的准确性,以图5所示的推耙横梁为例说明误差减小过程。根据圣维南原理,在两种不同但静力等效的载荷作用下,梁的两种载荷所导致的应力在距边界载荷位置足够远的地方相等。因此,未知边界载荷可等效为若干未知集中力。如图5所示,推耙机横梁的右端固定,另一端受5种集中力作用,为拉、弯和扭载荷。5个集中力包含4个未知变量,即轴向拉力F1,水平弯曲力F2,垂直弯曲力F3和扭矩的力偶F4。先用两个应变花测定了横梁表面的四个应变,然后建立了应变与载荷的关系式。采用C3D20R单元对推耙机横梁进行网格划分。横梁的材料为Q235钢材,钢材的主要参数列入表1。
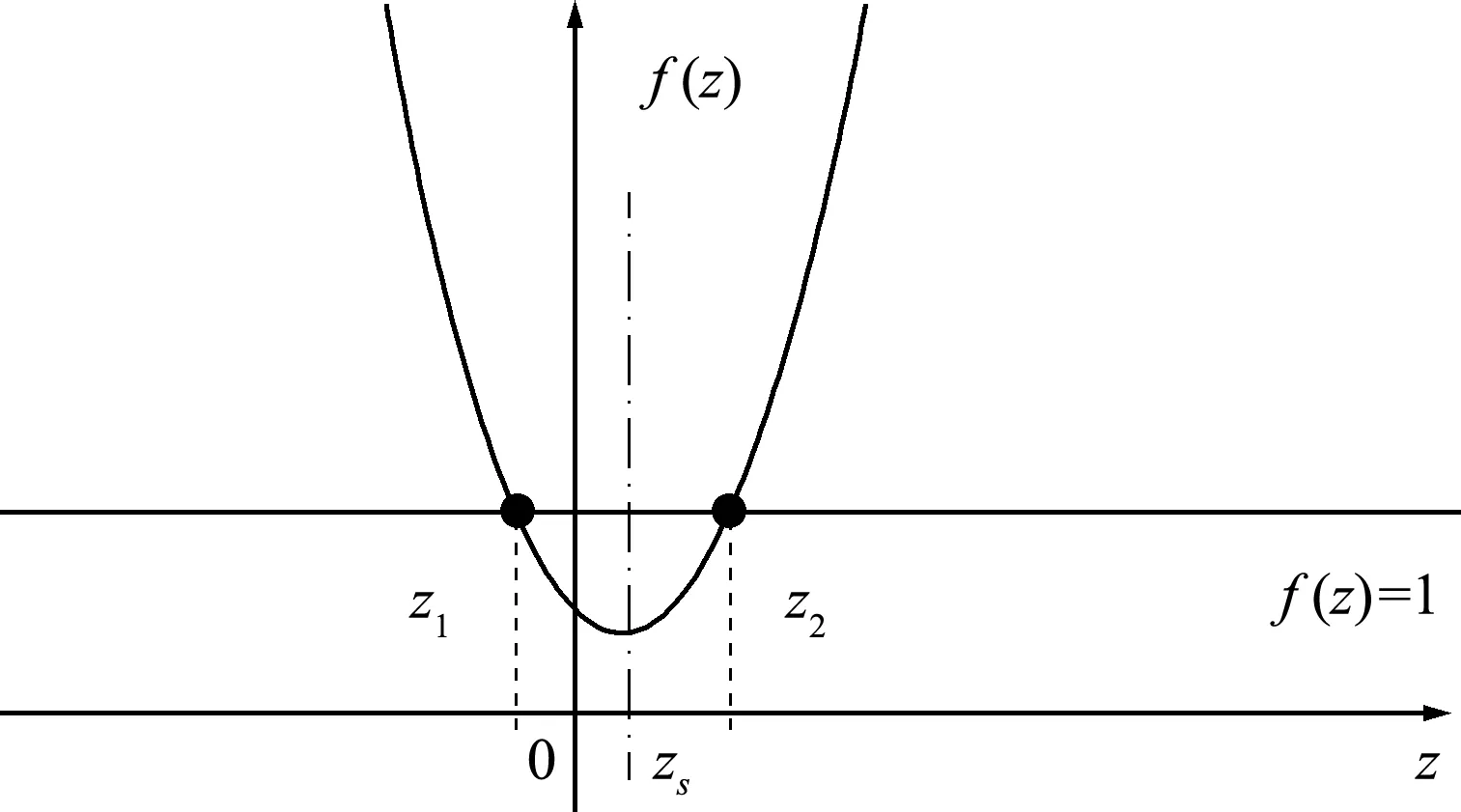
图4 误差函数单调特性
Fig.4 Monotonic property of the error function
采用仿真和测量相结合的方法对上述误差消减方法进行验证,流程如图6所示。首先,实测应变εm(表2)代入式(12)得到一组初始边界载荷,将计算得到的边界载荷(表3)假定为真实载荷Fr,将真实载荷Fr加载在横梁有限元模型上,然后导出应变εc(表4),称εc为计算应变。表3给出两种不同网格尺寸下计算得到的边界载荷,可以看出,由于采用了结构化六面体网格,继续缩小网格尺寸对于改善计算精度的效果已不明显,以下计算过程采用的网格尺寸均为14 mm。表2的εm和表4的εc不相等,这是由于误差因素引起的。为了避免这些误差,采用新的实测应变对边界载荷进行重新计算,并与有限元模型的初始载荷进行比较。图7所示的载荷是在理论数据εc中分别加入5%和10%的噪声,这些噪声用于验证测量误差相对于增加应变数的收敛性。当εc存在5%的噪声时,5~8组的新增应变片误差在区间[z1,z2]内,反求载荷误差与前一组应变相比会逐渐减小(图8)。换言之,当误差在[z1,z2]区间内时,更多的实测应变有助于提高求解精度。一些边界载荷如F4,对实测应变数据的分布更为敏感,即使应变超出上下界一小部分或位于边界附近,也可能偏离收敛趋势。为了避免采样点的偶然性,使用另外10组在不同时间点采样的应变数据进一步验证了该方法的有效性,如图9所示,由6应变计算的边界载荷比4应变更接近实际载荷(实际载荷为通过在横梁上贴应变片测量的载荷)。除不同时刻的验证外,本文还采用了不同时刻不同采样点(图10)和不同6+4采样数据组合(图11),来计算结构的边界载荷,其中图10和图11所用的数据采样点位置和时间相同,图10和图9所用的数据采样点位置和时间都不同。上述结果可进一步验证边界载荷反求结果收敛的一致性。
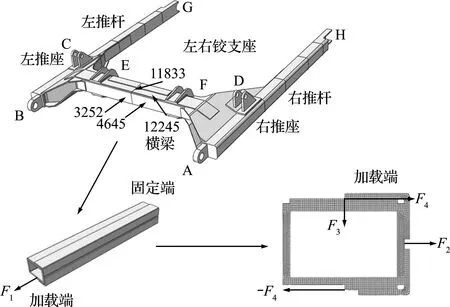
图5 局部结构分离
Fig.5 Local separated structure
表1 横梁材料属性
Tab.1 Beam material properties

材料密度/kg·m-3弹性模量/Pa泊松比σy/MPaσn/MPaQ23578002.1e110.3235350
表2 测量应变εm
Tab.2 Measured strainsεm
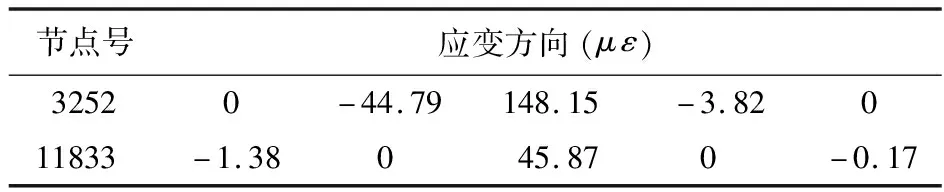
节点号应变方向(με)32520-44.79148.15-3.82011833-1.38045.870-0.17
表3 通过测量应变εm反求出的载荷
Tab.3 Boundary loads inversely calculated by measuring strainsεm
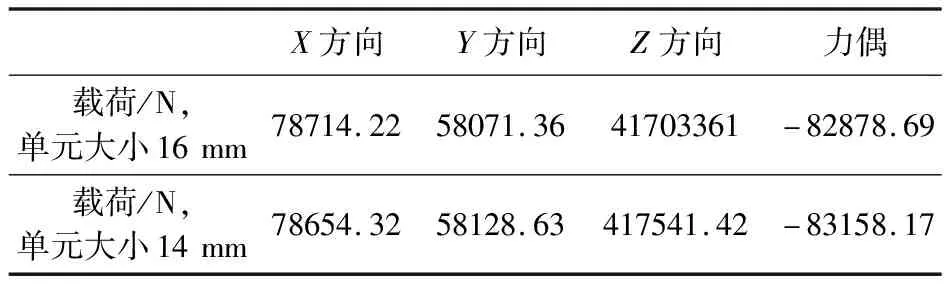
X方向Y方向Z方向力偶载荷/N,单元大小16mm78714.2258071.3641703361-82878.69载荷/N,单元大小14mm78654.3258128.63417541.42-83158.17
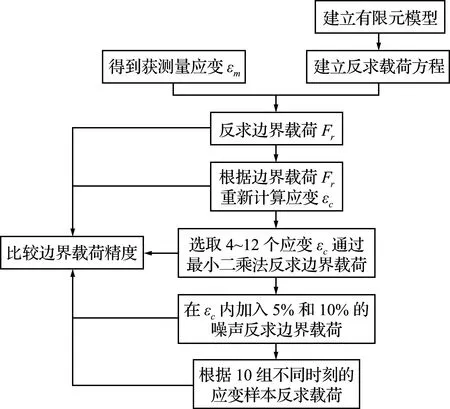
图6 验证流程
Fig.6 Verification flow chart
表4 FEM模型导出应变εc
Tab.4 Strainsεcexported from the FEM model

节点号应变方向(με)32520-69.68138.366-6.840118334.920-39.980-4.83122450193.57-579.693-17004645-38.440102.940-185.87
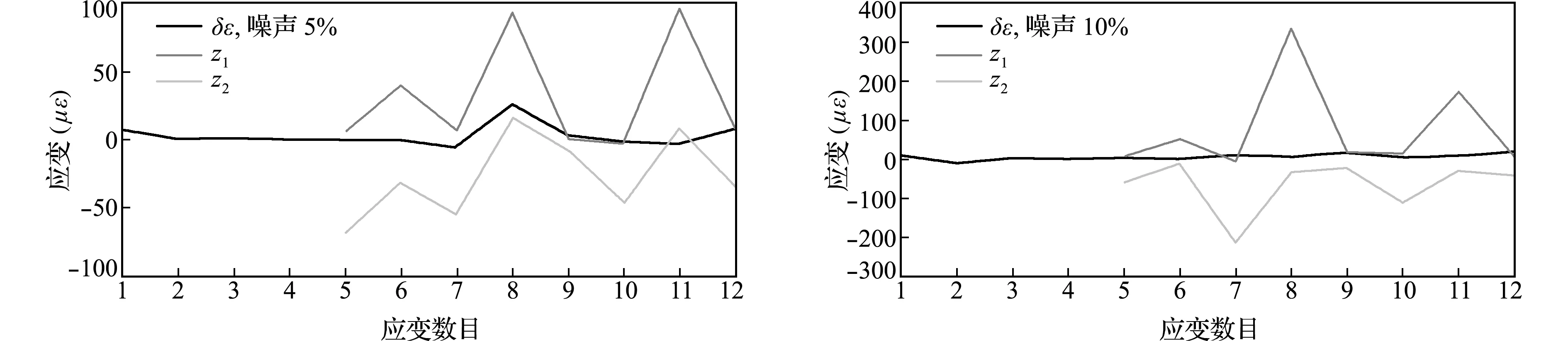
图7 应变误差
Fig.7 Strain errors
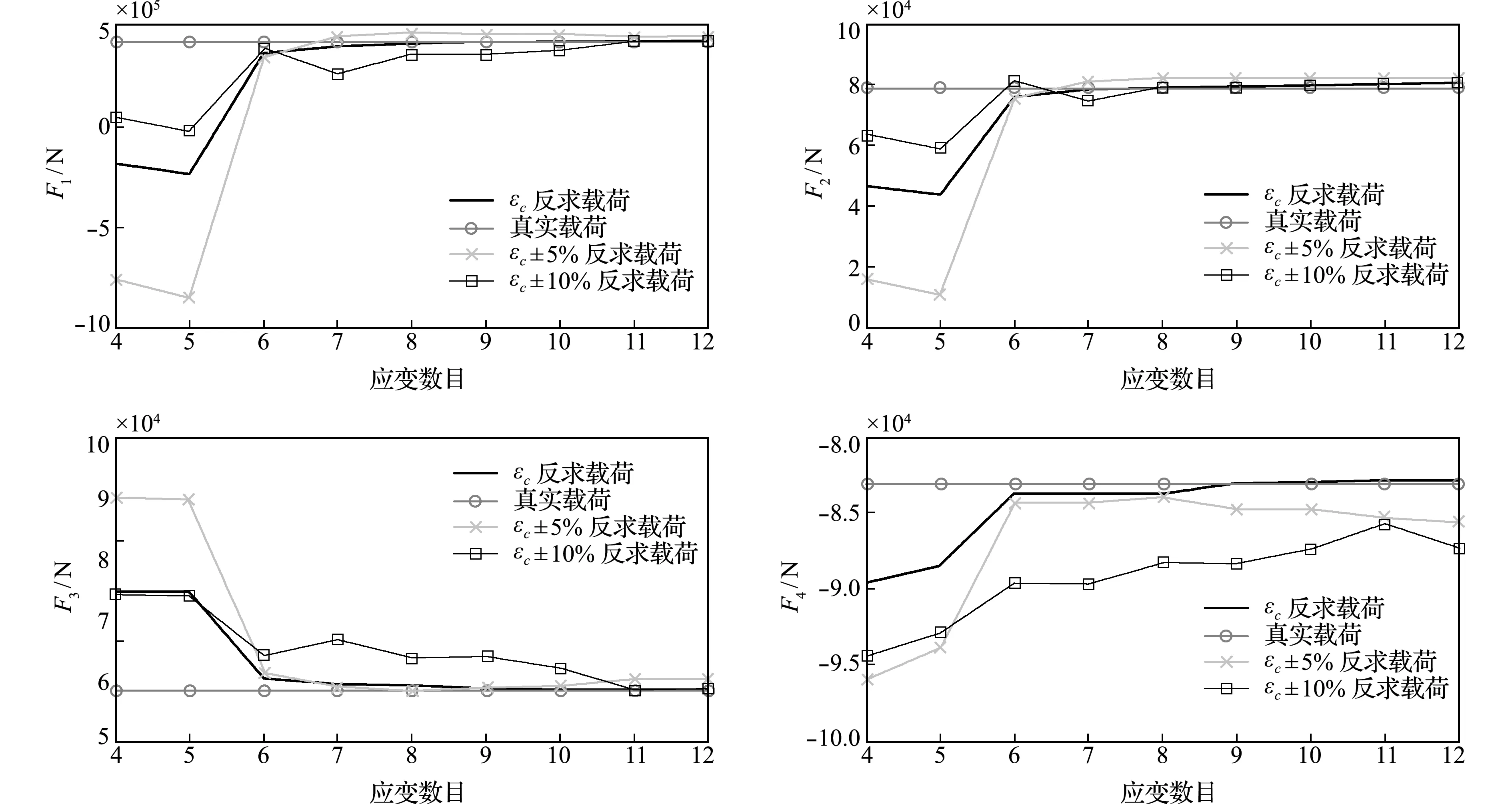
图8 不同应变数计算的边界载荷
Fig.8 Boundary loads calculated by different number of strains
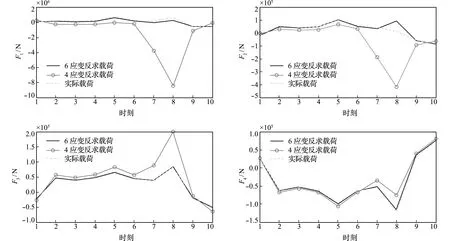
图9 根据10组不同时间点的采样数据计算边界载荷
Fig.9 Boundary loads calculated according to strains sampled at 10 different timepoints
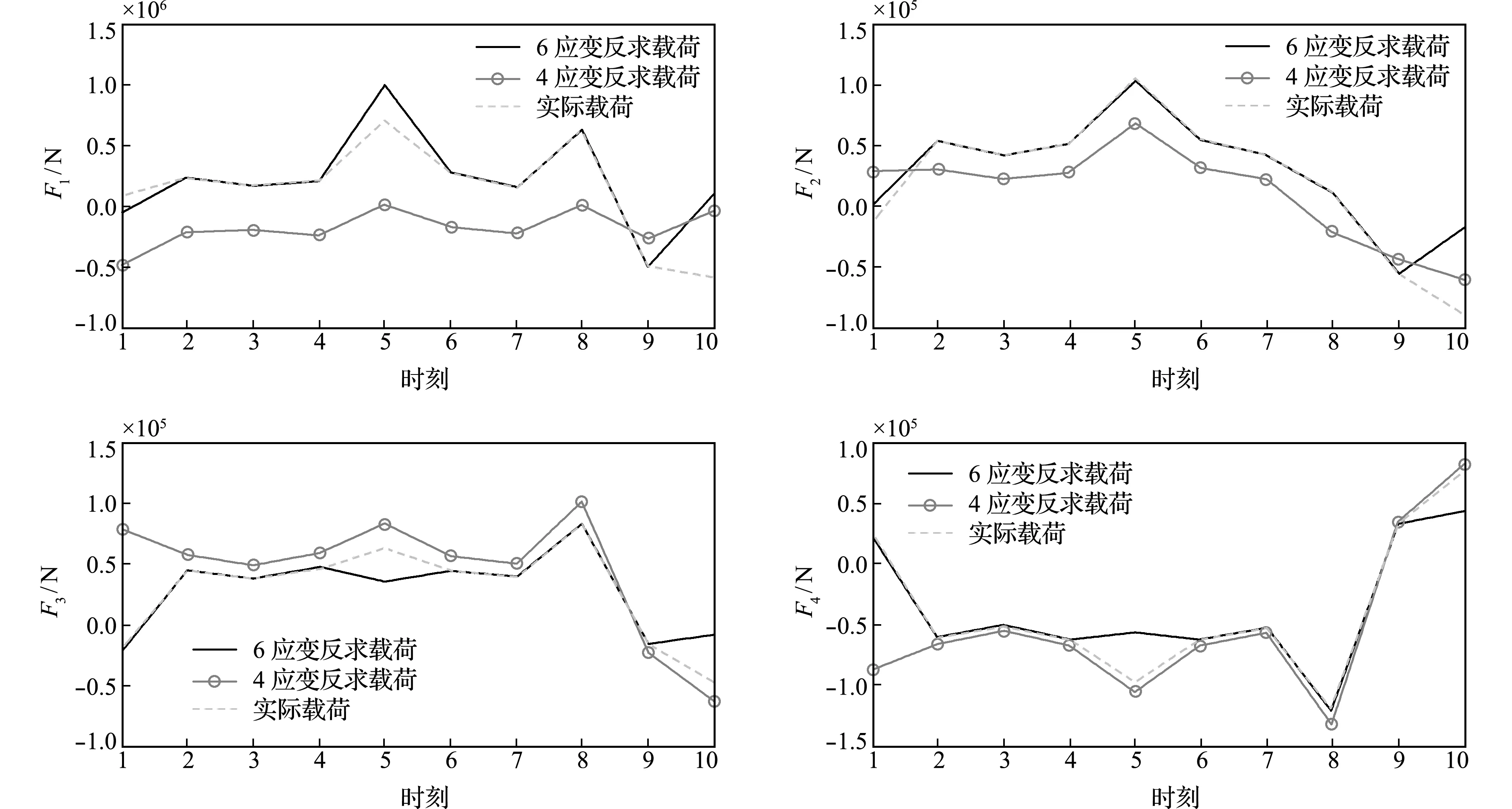
图10 在不同采样点(不同时刻)提取应变数据获得边界载荷
Fig.10 Boundary loads calculated by strains sampled at different locations and different timepoints
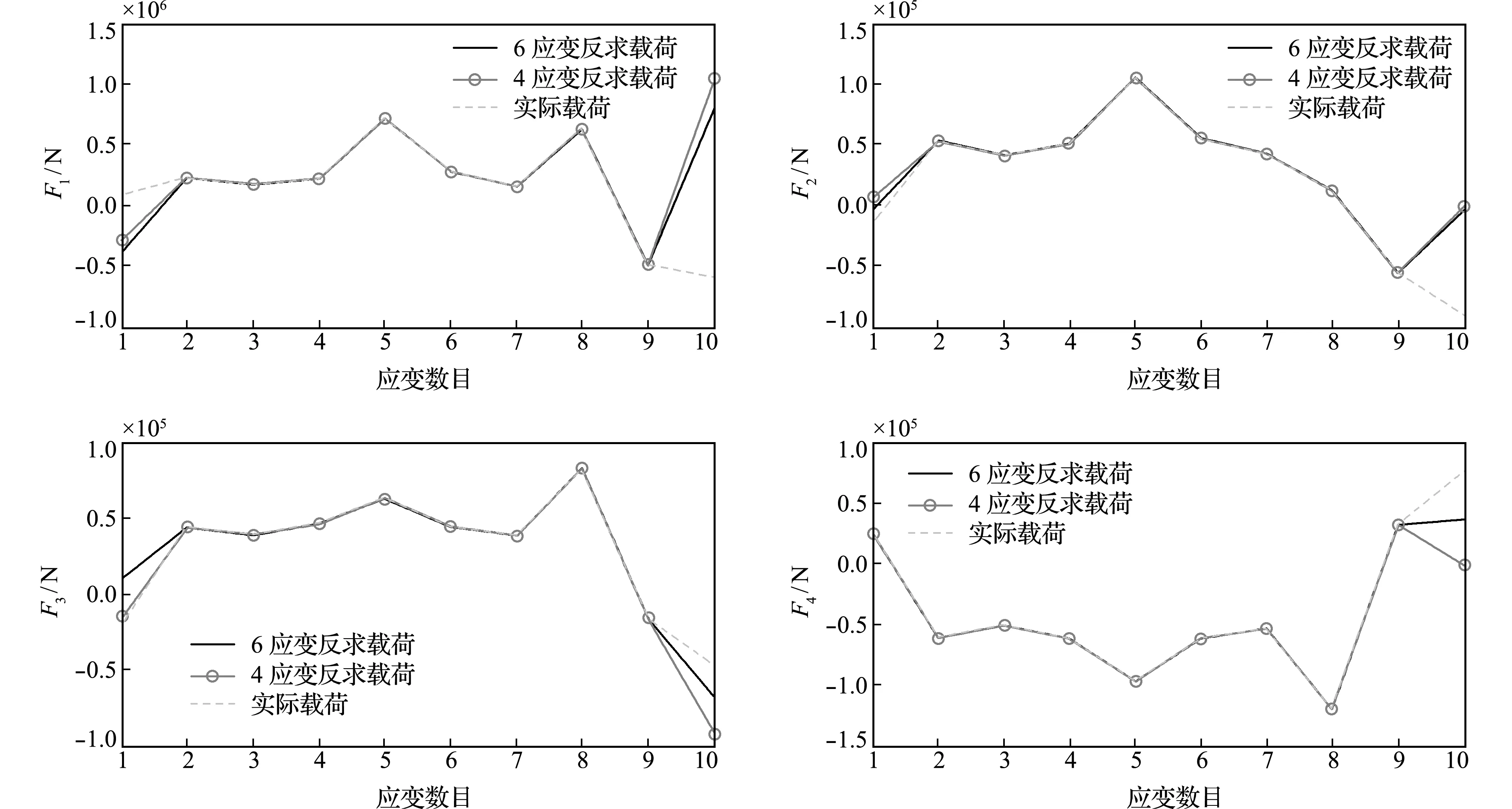
图11 不同6+4采样数据组合计算边界载荷
Fig.11 Boundary loads calculated by different 6+4 data combinations
4 结 论
依据圣维南原理,采用有限元法求得了局部分离结构的等效边界载荷。首先,推导了计算等效边界载荷的简化数学模型,避免了大量的数值计算;其次,提出了基于最小二乘的工程结构边界载荷反求误差消减方法。在今后的研究中,还需要在结构边界载荷的计算模型中将有限元模型误差和边界条件近似误差加以考虑,以便获得更加精确的结果。

