基于FEM 与集总参数法的热电制冷器数学建模方法研究

李 鹏

（株洲中车时代电气股份有限公司， 湖南 株洲 412001）

0 引言

热电制冷器（Thermoelectric Cooler，TEC）又称半导体制冷器，是一种主要根据帕尔贴效应制成的固体制冷器。准确的热电制冷器数学模型， 是研究和应用TEC 的基础。本文通过总结已有的数值分析方法，提出了有限元分析法与集总参数法，应用此两种分析方法，对四种不同面长比的热电制冷器在真空与空气中的制冷温度进行分析，并引入实验数据进行对比，旨在评估各分析方法的精度与适用范围。

1 热电制冷器理论模型

在热电制冷包含五种基本的物理效应： 塞贝克效应（Seebeck effect）、 珀耳帖效应 （Peltier effect）、 焦耳效应（Joule effect）、汤姆逊 效应（Thomson effect）、傅 里 叶 效 应（Fourier effect）。 各效应的物理层面原理在众多文献中都有详细阐述[2]，本文不再进行赘述。 其中汤姆逊效应产生的热交换属于二级效应， 一般情况下对计算结果影响较小。 在本文的模型中暂时忽略此效应。

N 型热电材料和P 型热电材料共同组成热电制冷器的基本单元，如图1（b）所示。忽略半导体电极在电流垂直平面内的温度差异，设纵向温度为T（x），其中，冷面处x=0，热面处x=L，则冷、热面的温度可表达如下：

取P 型半导体电极进行进一步分析， 假设电极流过电流为I，在Peltier effect 与Fourier effect 共同作用下，半导体电极冷面的制冷量qP为：

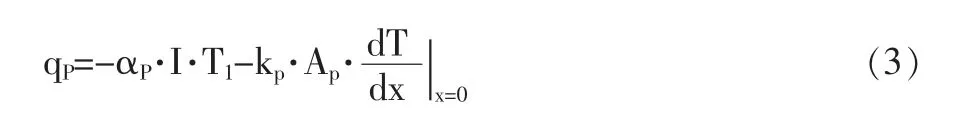
式中，αP—seebeck 系数（V/K）；kP—热导率（W/（m·K））。AP—P 型半导体材料的横截面面积（m2）。现计算电极在电流方向的温度分布，在电流流动方向上取一微元，如图1（c）所示，应用能量守恒、傅立叶导热定律及焦耳热定律，可得等式（4）与式（5）。

式中，ρP—热电材料电阻率 （Ω·m）， 综合式 （4）、式（5，）可得：

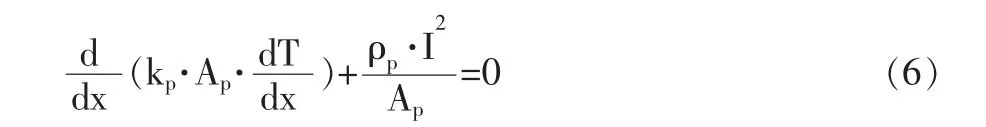
进一步假设：TEC 冷、热端温差不大，热电单元具有常物性，将式（1）～式3 作为求解边界条件，解微分方程式（6），可得如下形式等式：

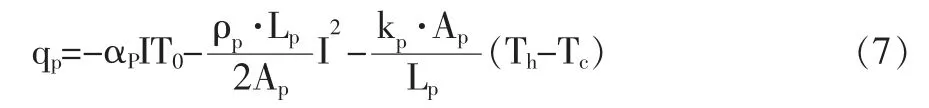
同理可得N 型半导体材料在冷面的制冷量qN：

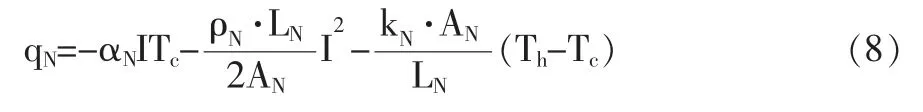
N、P 型热电偶对的总制冷量qc为：

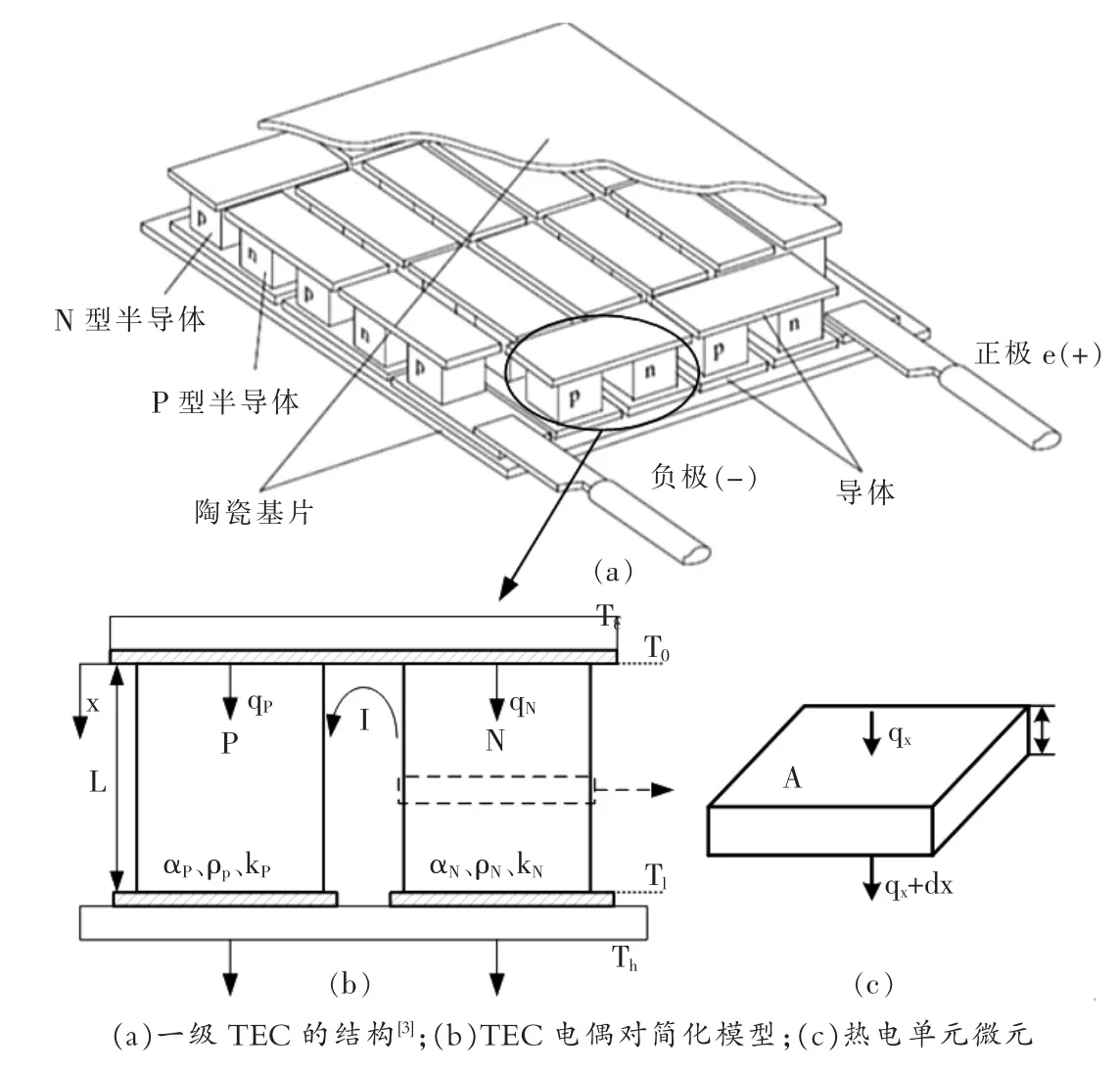
图1 TEC 模型示意图

假定N、P 热电材料具有类似物性（Similar Materials）[3]，式（9）可进一步改写为如下形式：

TEC 的电压U、输入功率w、热面逸散热量qh以及制冷系数（Coefficient of Performance，COP）分别为：

2 热电制冷器数值分析方法

2.1 有限元分析法

有限元分析法通过将电极在温度梯度方向进行微元划分，微元尺度达到一定的细化程度后，每个微元上的温差就可以不进行考虑，从而进行常物性处理。

电极在温度梯度方向被平均分成m 份，令：第j 个部分的底面温度为Tj，顶面温度为Tj+1，第j 个部分的物理特征参数分别为αj、ρj、kj，各自取值如下：

式（10）可进一步调整为：

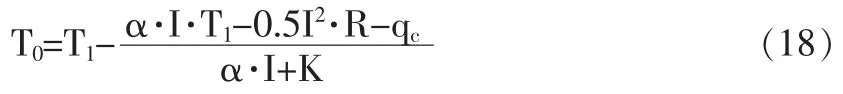
基于此， Tj与Tj+1、Qj与Qj+1之间的关系如下：

Wj为第j 个微元消耗的电功率，其定义为：

热电单元冷面的温度即为第m 个微元顶面的温度：

陶瓷基板的热阻在分析过程中不可忽略，TEC 性能分析需要对陶瓷基板热阻进行考虑。 本文使用Rcm表示陶瓷基板热阻，Rcm的定义方程如下：

式中：H—陶瓷基板厚度 （m）；kcm—陶瓷基板热传导系数（W/（m·K））；Acm—热电电极的横截面积，金属导体的传导热阻和金属焊层的接触热阻均相对较小， 通过增加修正系数z 进行考量，z 的取值范围为5%～15%。 T1与Th之间的关系为：

T0与Tc之间的关系为：

由于qc在多数情况下取值都较小，故可近似认为：

2.2 集总参数法

集总参数法的核心思想是：对将方程式（4）～（6）中的热电材料物性参数与温度的关系进行解耦， 具体操作方法为使用一组合适的常物性参数作为热电材料物性，代入微分方程，进行化简求解。

TEC 工作时， 热电电极的温度在热面温度Th与制冷温度Tc之间连续变化， 为筛选出合适的常物性参数计算方法， 提出三种不同计算策略： ①使用TEC 热面的温度（Th）确定物性参数；②使用TEC 冷、热面温度的平均值（Tavg）确定物性参数；③使用冷、热面温度物性参数的数值平均值（Pavg）作为需要的物性参数。 现将此三种方法的计算结果与实测数据进行对比从而确定最佳物性参数计算方法。

3 计算方法对比分析

为对计算方法进行验证和筛选， 提取4 种不同面/长比（λ=A/L）的热电制冷器参数，应用两种分析方法，进行对比分析。 I、II、III、IV 分别作为这4 种TEC 的代号，I 号TEC 是参考文献[1]所使用的TEC，II 为Marlow 公司型号为SP2664 制冷器，III 和IV 均为RMT Ltd 公司产品，其型号分别为1MC06－142－05 和1MC06－142－12 的。

I 号TEC 的分析结果表明：有限元分析法计算结果与实验结果符合程度非常好： 最大制冷温差的计算值与实验值误差为1.5K，相对误差为1.75%；最大电流的计算值与实验值误差为0.07A，相对误差为3.2%；集总参数法三种策略的计算结果都与实验结果有较大偏差， 最大制冷温差的相对误差的最大值为12.1%， 最大电流的相对误差最大值为19.1%。

II 号TEC 的分析结果表明：在集总参数法策略A、B、C 中，策略A 的计算结果与实验结果符合程度最高。 最大制冷温差、最大电流两项指标的计算结果与实验数据之间的相对误差均＜2%。 策略B、C 的计算误差均大于策略A，而有限分析法在该TEC 计算中，得到了最大的计算误差。

III、IV 号TEC 有真空与普通大气环境两种实验数据。III、IV 号TEC 的分析结果表明：有限元分析法适用于真空环境中TEC 性能分析，计算结果与真空环境中的实验结果相对误差＜4%； 集总参数法则适用于普通大气环境中TEC 性能分析，且策略A 为更优参数确定策略。 面长较大的III 号TEC 的计算结果与大气环境中的实验数据相对误差＜2%；面长比相对较小的IV 号TEC 的计算结果与大气环境中的实验数据相对误差＜5%。

4 结论

有限元分析法适合对TEC 性能进行精确分析，在真空环境下，一级TEC 的计算制冷温差与实测制冷温差的相对误差＜4%，该方法的优势在于：将陶瓷基板、金属导体及焊接层的热阻均纳入了计算过程， 模型精确度不受热电单元面长比的影响， 适用于各种TEC 的性能计算。其缺点是计算复杂程度较高， 为考虑制冷器与空气的偶合关系， 故对于应用于气体环境中制冷器的性能计算会优于实验测试结果。

在集总参数法的三种参数计算策略中， 策略1 的适应性最强， 适用于大气环境中TEC 的性能分析与计算，TEC 的计算制冷温差与实测制冷温差的相对误差＜5%，由于可以获取解析解，其计算过程十分简便，还能进一步得到TEC 不同约束条件下的最优性能参数解析解。 其缺点是暂未考虑陶瓷基板与热电电极之间的部分热阻，当热电电极面长比减小、热面功率密度降低时，会出现计算结果较实验值偏小的现象。