小样本加速寿命试验方法

傅惠民， 文歆磊， 吴 琼

（1.北京航空航天大学 小样本技术研究中心， 北京 100191； 2.北京空间飞行器总体设计部， 北京 100094）

0 引言

随着产品寿命和可靠性的不断提高， 加速寿命试验应用越来越广泛。 对于工程上常见的加速系数未知的情况，一般需在多个加速应力水平下进行寿命试验，并采用最佳线性无偏估计（BLUEs）等方法进行统计分析[1]，这不仅导致试验工作量较大，而且在较低的加速应力水平还会出现不完全数据，甚至无失效数据，无法进行统计分析。

为此，本文给出一种小样本加速寿命试验方法，只需在两个加速应力水平下进行加速寿命试验， 即可确定加速系数，并推断出产品在正常使用应力水平下高置信度、高可靠度的寿命单侧置信下限。 与传统方法相比，本文方法在精度相同的条件下可以节省大量试验， 而在试验量相同时则可提高精度。

1 小样本加速系数

设S 为广义应力（温度、湿度、电应力、载荷、载荷谱、环境谱等），为了确定产品在正常使用应力水平S0下可靠寿命tR的置信水平为γ 的单侧置信下限tRL， 采用加速寿命试验，以解决试验时间长、成本高的问题。

现选取一个加速应力水平S2，按传统方法，加速应力水平S2对应力水平S0的加速系数为[1]

式中，tR，0和tR，2分别为产品在S0和S2下可靠度为R 的寿命。理论上还可以证明，对于指数分布、两参数Weibull 分布、对数正态分布等，加速系数τ2～0与可靠度R 无关，可以用寿命均值或特征寿命代替tR，0和tR，2。

然而，tR，0和tR，2均为真值，工程上无法求得，只能得到其估计值，特别是在小样本情况下，加速系数往往与可靠度R 和置信水平γ 都有关，因此定义小样本加速系数τ～2～0为

式中，tRL，0和tRL，2分别为产品在S0和S2下置信水平为γ的可靠寿命tR，0和tR，2的单侧置信下限。由此可知，采用式（2）给出的加速系数进行加速寿命试验，并评估产品在正常使用应力水平S0下置信水平为γ、 可靠度为R 的寿命单侧置信下限tRL，0，可以减小误差，提高精度。

1.1 基于阿伦尼斯模型的加速系数

当温度作为加速应力时， 加速方程通常可采用阿伦尼斯模型，即有

式中，m 和C 为待定参数。 将式（3）代入可得

再将式（4）和式（5）代入式（2），求得加速应力水平S2对应力水平S0的小样本加速系数为

1.2 基于逆幂律模型的加速系数

当电应力（电压、电流、功率等）、载荷、湿度等作为加速应力时，其加速方程为

式中，m 和C 为待定参数。 将式（3）代入可得

根据式（2）和式（7），可以得到加速应力水平S2对应力水平S0的小样本加速系数～ 为

1.3 基于指数模型的加速系数

电应力、 载荷作为加速应力， 有时也可采用指数模型，其加速方程为

式中，m 和C 为待定参数。 将式（3）代入可得

同样，求得加速应力水平S2对应力水平S0的小样本加速系数0为

在失效机理不变的前提下，加速应力水平S2应尽可能选得大一些，加速效果会更加明显，而且在高加速应力水平下，产品更容易暴露其存在的缺陷和薄弱环节。加速应力水平S1也尽可能选得大一些，但应与S2有一定的差距，避免寿命分散性干扰加速应力水平S2对S1的加速系数τ～2～1。

2 可靠寿命和可靠度评估

2.1 基于阿伦尼斯模型的情况

当温度作为加速应力时，由式（6）可知，产品在正常应力S0下置信水平为γ、 可靠度为R 的寿命单侧置信下限由下式计算

式中

2.2 基于逆幂律模型的情况

当电应力、载荷、湿度等作为加速应力时，由式（9）可知，产品在正常应力S0下置信水平为γ、可靠度为R 的寿命单侧置信下限tRL，0仍由式（13）计算，此时

2.3 基于指数模型的情况

当采用指数模型作为加速方程时，由式（12）可知，产品在正常应力S0下置信水平为γ、 可靠度为R 的寿命单侧置信下限tRL，0仍由式（13）给出，此时

根据置信限等同性原理可知，产品在给定应力S0下寿命t 处置信水平为γ 的可靠度单侧置信下限RL，0也可以通过式（13）求得。 具体只需在式（13）中令tRL，0=t，并求解出相应的可靠度， 即为产品在给定应力S0下寿命t 处置信水平为γ 的可靠度单侧置信下限RL，0，详见下面两节。

3 小样本定时截尾加速试验

设产品在应力水平S 下的寿命t 服从两参数Weibull 分布

式中，α 为形状参数，不随S 变化；β（S）为尺度参数，是S的函数。

设有n 个试样进行定时截尾试验， 得到r 个失效数据t1，t2，…，tr，n-r 个未失效数据t0，则其置信度为γ、可靠度为R 的可靠寿命tR的单侧置信下限为[2]

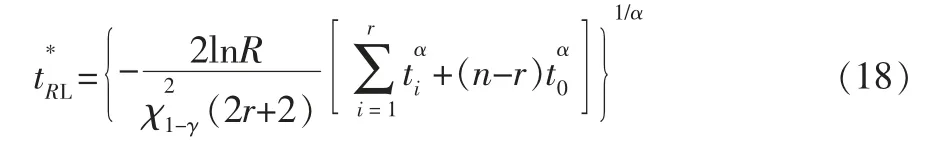
工程实际中，由于形状参数α 通常未知，还不能直接用式（18）求得可靠寿命的置信下限。 但是在多数情况下能够知道α≥α0，即形状参数的下限α0已知（例如，对于铝合金结构，α0=4； 钛合金结构，α0=3； 钢结构，α0=2.2）[3]。可以证明[2]，若给定的R 满足

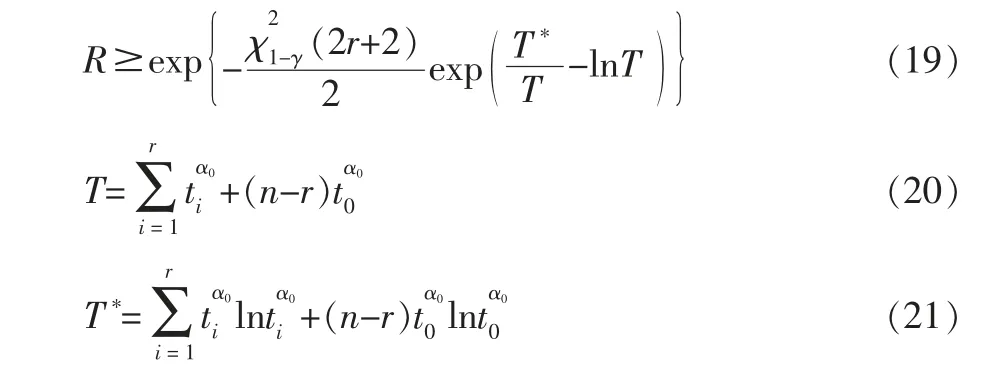
则置信水平为γ 的可靠寿命tR的单侧置信下限为

即

3.1 加速系数

根据式（3）和式（22），求得加速应力水平S2对加速应力水平S1的加速系数为

式中，T1和T2分别是应力水平S1和S2下的广义总试验时间，可通过式（20）求得；r1和r2分别是S1和S2下的失效数，并且S1和S2下的试样数n 和截止时间t0均相同。

将式（24）代入式（6）、式（9）和式（12），即可得到定时截尾试验各加速方程下的加速系数。

3.2 可靠寿命置信下限

根据式（13），求得产品在正常应力S0下置信水平为γ、可靠度为R 的寿命单侧置信下限为

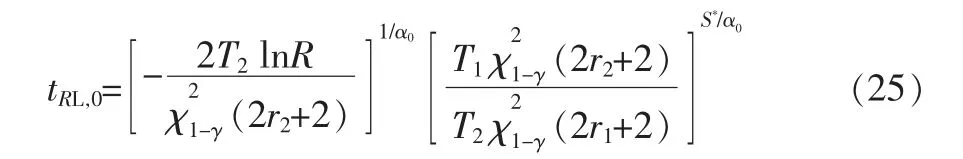
对于阿伦尼斯模型、逆幂律模型和指数模型，式中S*分别由式（14）～式（16）给出。

3.3 可靠度置信下限

根据置信限等同性原理，由式（25）可以求得产品在给定应力S0下寿命t 处置信水平为γ 的可靠度R 的单侧置信下限

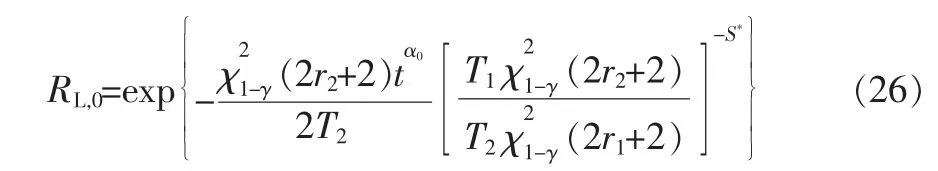
式中，S*分别由式（14）～式（16）给出。

4 小样本定数截尾加速试验

设产品在应力水平S 下的寿命t 服从式（17）给出的两参数Weibull 分布。 现对n 个试样开展定数截尾试验，得到r 个失效数据t1≤t2≤…≤tr，剩余n-r 个试样在试验停止时间tr处仍未失效。 则该产品的置信度为γ、可靠度为R 的可靠寿命tR的单侧置信下限为

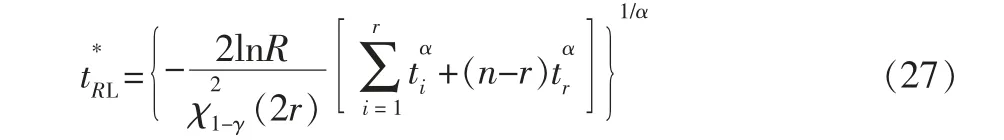
同样，形状参数α 通常未知，但是其下限α0已有大量统计资料[3]。 可以证明，若给定的R 满足

则置信水平为γ 的可靠寿命tR的单侧置信下限为

即式（23）成立。

4.1 加速系数

根据式（3）和式（31），求得加速应力水平S2对加速应力水平S1的加速系数为

式中，T1和T2分别是应力水平S1和S2下的广义总试验时间，可通过式（29）求得；S1和S2下的失效数r 和试样数n 均相同。

将式（32）代入式（6）、式（9）和式（12），即可得到定数截尾试验各加速方程下的加速系数。

4.2 可靠寿命置信下限

根据式（13），求得产品在正常应力S0下置信水平为γ、可靠度为R 的寿命单侧置信下限为

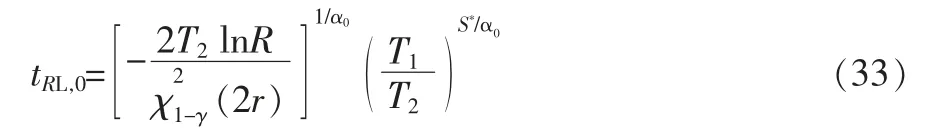
对于不同的加速模型，S*分别由式（14）～式（16）给出。

4.3 可靠度置信下限

根据置信限等同性原理，由式（33）求得产品在给定应力S0下寿命t 处置信水平为γ 的可靠度R 的单侧置信下限为

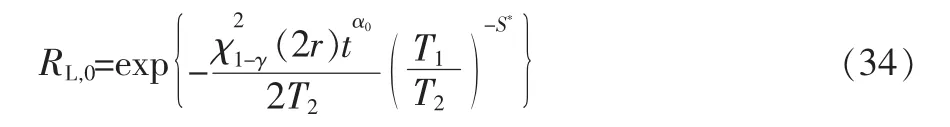
式中，S*分别由式（14）～式（16）给出。

5 其他情况

当产品寿命服从对数正态分布时，对于完全数据，可采用文献[4]方法计算加速应力水平S1和S2下置信水平为γ、可靠度为R 的寿命单侧置信下限；对于截尾数据和不完全数据，可采用文献[5]和文献[6]方法计算置信水平为γ 的可靠寿命单侧置信下限。

对于两参数Weibull 分布且形状参数下限α0未知，以及其他连续分布和数据类型的情况，均可采用文献[5]和文献[6]方法计算置信水平为γ 的可靠寿命单侧置信下限。

6 算例

6.1 算例1

表1 给出了某产品在加速应力水平S1=450MPa 和S2=500MPa 下的寿命数据， 试验截尾时间均为106循环。已知该产品的寿命服从两参数Weibull 分布，取α0=3。 要求确定该产品在正常使用应力水平S0=150MPa 下置信水平γ=0.9、可靠度R=0.999 的寿命单侧置信下限。

表1 某产品定时截尾加速寿命试验数据

由于该试验以载荷作为加速应力， 因此可采用逆幂律模型作为加速方程，根据式（15）和式（25），求得S0下置信水平γ=0.9、可靠度R=0.999 的寿命置信下限为

6.2 算例2

某航天零件需在40℃下连续工作15 年，经分析可知其关键失效模式为应力松弛， 当载荷损失率达到规定的阈值时，即可认为失效。为验证该零件的可靠度能否满足“R=0.999（置信水平为γ=0.9）”的指标要求，在180℃和220℃下分别投入一个试样进行高温应力松弛试验。

虽然采用了高温加速试验，但是试验至400h 时，试样的退化量仍然较小。 此时，采用文献[7]提出的幂函数退化曲线快速测试方法，外推得到180℃和220℃下的寿命分别为3770h 和960h。 已知该零件由高强度钢制成，其寿命服从两参数Weibull 分布，因此可取α0=2.2。 根据式（14）和式（34），求得40℃下15 年寿命的可靠度单侧置信下限为

由此可知，该零件的可靠性能够满足指标要求。

7 结论

提出一种小样本加速寿命试验方法，只需在两个加速应力水平下进行加速寿命试验，即可对产品在正常使用条件下的可靠寿命和可靠度进行评估。 与传统方法相比，可以节省大量试验，并且对Weibull 分布、对数正态分布等任意连续分布以及完全数据、截尾数据、不完全数据均适用。

本文采用的加速系数因考虑了可靠度和置信水平的影响，所以在可靠性评估中可以有效提高精度。文中详细讨论了Weibull 分布定时截尾和定数截尾两种工程上常见的加速寿命试验，给出了加速系数、可靠寿命和可靠度单侧置信下限公式。对于加速退化试验，当试样在加速应力水平下长期试验仍然不失效时，可以结合文献[7]或文献[8]方法进行快速测试。

文中讨论了工程上常见的三种加速模型， 对于其他加速模型本文方法也同样适用。 特别是对于应力水平与寿命在双对数坐标系或半对数坐标系中并非线性关系，而是呈现出先快速下降再缓慢下降的“先快后慢”规律的情况， 可直接采用文中方法和三个加速模型进行可靠性评估，且结果偏于保守，工程上安全可用。