基于有限元方法的动车组车轮安全性能评估

贺 妍

（智奇铁路设备有限公司研发中心，山西 太原 030032）

随着动车组运行速度的不断提高，对其走行部件安全性能的要求也不断提高，科学合理地评估动车组车轮安全性能势在必行。动车组车轮在结构上虽然为一个整体，但各部位结构差异较大，在运行过程中各部位所起的作用也不相同，而且车轮在实际运行过程中受力复杂，既有轮轨间的接触力（包括横向力和纵向力），还有轮轴配合部位产生的约束力及通过轴承传递的整个车体的重量（垂向力），上述各种载荷还会因线路、速度及外界环境等因素的变化而发生变化，因此，对车轮安全性能进行评估难度较大，欧洲标准[1]推荐采用有限元方法对车轮辐板部位的安全性能进行评估。

基于欧洲标准，为满足车轮运营安全性，本文提出了基于有限元分析软件ANSYS 的动车组车轮有限元模型的建立及静强度和疲劳强度的分析计算，从而对车轮安全性能进行评估。首先根据车轮名义尺寸建立车轮的有限元模型，然后根据车轮结构对称性确定加载平面并按照标准给出的工况及工况载荷对各加载面进行加载计算，通过有限元计算结果并结合车轮结构特点选择合理的强度准则对车轮进行静强度及疲劳强度计算，从而得出车轮强度最薄弱的部位，在该部位附近区域粘贴应变片对该实体车轮进行疲劳试验验证，将疲劳试验的结果与有限元计算结果进行比较，比较结果验证了有限元计算结果的正确性。

1 有限元模型的建立

1.1 模型的建立

以某型号动车组动车车轮为例，依据车轮产品图纸及材料特性，参数弹性模量E为210 MPa，剪切应变γ 为0．29[2]，用ANSYS PLANE182 平面轴对称单元建立车轮的二维有限元模型，见图1。考虑到车轮毂孔部位的圆弧仅为满足结构或使用上的要求而设置，并非根据强度要求而存在，为了便于有限元网格的划分，将该部位的圆弧过渡简化为直线连接过渡。整个车轮的三维有限元模型采用ANSYS SOLID 185 结构单元[3]，见第48 页图2。

图1 车轮的二维有限元模型

图2 车轮的三维有限元模型

1.2 载荷施加

为了模拟实际运行工况，在车轮毂孔部位建立模拟车轴[4-5]，用于建立实际工况下轮轴配合部位的约束。在有限元模型中，轮轴之间的配合作用通过接触单元contact172 和目标单元target170[6]进行模拟，通过建立接触对设定压装过盈量的值[7]从而施加该部位的配合约束，轮轴间摩擦系数为0．12[8]。

根据车轮对称性确定加载平面[9]，按照标准给出的4 种载荷工况[1]、各工况对应的载荷值[7]及载荷加载位置对各加载平面进行加载，载荷以集中力的方式施加在相应的位置[10]；在模拟车轴两端施加径向、周向约束，其中一端施加轴向约束；离心力的作用根据车轮设计速度[7]以角速度方式施加。

2 强度计算

2.1 静强度计算

由FEM 计算得到的静态验证结果通过第四强度理论[11]可以计算出安全系数，计算公式为

式中：Re为车轮材料米塞斯等效应力极限值[1]，MPa；σeqv为根据有限元结果计算的米塞斯等效应力值其中，σ1，σ2，σ3为在已知载荷工况和径向位置的节点的主应力。

按照式（1），可以计算出4 种载荷工况以最大过盈量和有离心力作用下的车轮静强度安全系数，见表1。

表1 车轮静态验证结果

从表1 的计算结果可以看出，车轮静强度在标准[1]要求的范围内，即静强度计算结果满足车轮安全性能要求。

2.2 疲劳强度计算

疲劳验证考虑了3 种载荷工况、最大压装过盈量的影响及离心力的影响。对车轮加载截面辐板表面内、外侧节点以及直径25 的孔的节点进行验证。

综合3 种载荷工况、多个载荷平面[9]和多个圆周位置上的评估，并考虑到模型的几何对称，能够确定360°的载荷循环。采用笛卡尔坐标系，X为径向、Y为周向、Z为轴向，车轮辐板表面节点的疲劳验证具体方法如下。

2.2.1 节点应力计算

通过有限元验证结果找出各节点在所有载荷工况和加载面上的σ1max，σ2max和σ3max及其方向余弦，计 算 各 节 点 对 应 的σ11max，σ12max，σ21max，σ22max和σ33max的数值并找出其方向余弦；对于所有要考虑的载荷工况和加载面，应力张量在σ11max方向投影，得到应力最小值σ11min；按照同样的步骤方法计算σ12max，σ21max，σ22max和σ33max，进而求得σ12min，σ21min，σ22min和σ33min。其中，σ11max为节点在所有载荷工况和加载面中最大的σ1；σ12max为节点在σ11max工况下的σ2；σ21max为节点在σ22max工况下的σ1；σ22max为节点所有载荷工况和加载面中最大的σ2；σ33max为节点所有载荷工况和加载面中最大的σ3。加载面通常用角度θ 表示载荷平面的角度位置，假设顺时针方向为正，角度θ 是正数。

2.2.2 疲劳分析

对于轴对称车轮按照单轴疲劳准则（High 形式Goodman 评价准则）进行强度校核，对于非轴对称车轮，比如车轮辐板孔部位，按照多轴疲劳准则（Crossland criterion 评价准则）[12]进行强度校核。

除辐板孔表面节点外，辐板表面其他节点的应力循环为单轴应力循环，每个待考察节点的应力循环见表2。

表2 单轴应力循环

结合该型号车轮的材料性能参数（材料的米塞斯等效应力极限值以及辐板部位对称循环疲劳极限[13]），将各节点在所有载荷工况下的有限元计算结果按照High 形式Goodman 评价准则进行疲劳计算，从而得到辐板内、外侧表面每个考察节点的安全系数η11，η12，η21，η22和η33，辐板内、外表面节点的安全系数轮廓见第49 页图3-a、图3-b 及图4-a、图4-b。

车轮辐板孔表面节点的疲劳验证，采用克罗斯兰准则（Crossland criterion）对表面多轴应力进行分析，用最大应力和安全指数τott，a（动力学八面体剪应力）表示为

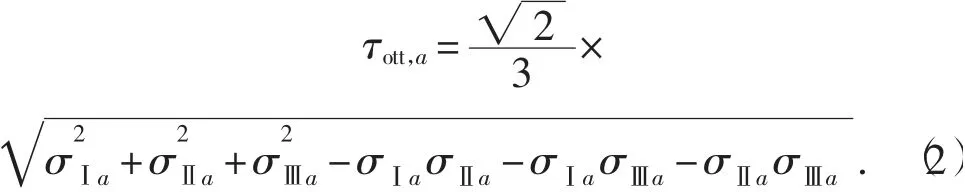
式中：σⅠa，σⅡa，σⅢa为所有涉及到的载荷循环的主应力幅。

图3 辐板内侧验证节点安全系数轮廓图

图4 辐板外侧验证节点安全系数轮廓图

将τott，a与一个极限量比较，该极限量取决于材料特性和最大第一不变线性函数IⅠ，max，IⅠ，max的表达式为

式中：σⅠ，max，σⅡ，max，σⅢ，max为所有涉及到的载荷循环的主应力的最大值。

克罗斯兰准则公式表示为

式中：常量B和β[14]取决于材料特性，

安全系数η1和η2为

将辐板孔表面节点的有限元计算结果按照上述克罗斯兰准则（Crossland criterion）进行计算，可以得出辐板孔表面各个节点的安全系数，见表3；辐板孔表面验证节点的克罗斯兰图见第50 页图5。

表3 辐板孔表面各个节点的安全系数

由以上疲劳安全系数计算结果可以看出，辐板内侧在节点21446，半径为213．7 mm 位置，应力最大，安全系数最小，最小安全系数η12（等于η22）为1．67；辐板外侧在节点21429，半径为215．1 mm位置，应力最大，安全系数最小，最小安全系数η12（等于η22）为1．66；辐板孔位置最小安全系数η2为2．26。可见车轮疲劳强度满足标准要求，而且可以得出，安全系数最小的位置位于车轮径向约213～216 mm 之间，该部位为车轮毂孔和辐板过渡区域。本文中采用的车轮、车轮外侧毂孔和辐板过渡区域安全系数最小，因此，在该型号车轮外侧毂孔和辐板过渡圆弧位置（半径为215．1 mm）附近区域粘贴应变片进行疲劳试验验证。

图5 辐板孔表面验证节点的克罗斯兰图

3 疲劳试验验证

根据车轮产品标准[2]推荐的试验方法，采用与标准相似的试验台，对车轮安全系数最小位置区域粘贴应变片进行全尺寸疲劳验证。

3.1 应变片粘贴

在疲劳试验中，用应变片测量设备[14-15]测量应变以测定施加在车轮上的应力。应变片粘贴在图6所示的车轮外侧应力最大、径向位置为215．1 mm对应的点上。在该点处使用3/120RY101 型应变花[14]（3 个栅丝，阻值为120 Ω），一方面，可以测定车轮表面上的所有应力分量，另一方面，可以消除应力分量计算过程中的角度误差。使用应变链可以发现20 mm 长度方向上的应变趋势和数值。车轴顶部轴颈的电机使偏心块旋转，在车轴上进而在车轮上产生弯矩。使用应变片测量车轮辐板的应变进而测定应力。偏心块的转速需进行准确的调节以便在车轮辐板上获得目标应力值。

图6 应变片粘贴位置

图7 轮轴全尺寸疲劳试验台安装示意图

在将试验轮对装到试验台上后，在车轮辐板-毂孔应力最大位置施加应力幅值σrada为240 MPa 的径向应力，循环107次。

试验结束后，对车轮表面进行磁粉探伤检测[17]，检测结果显示在检测部位未发现任何裂纹症状，见图8；证明车轮在应力幅值等于240 MPa 的对称循环应力作用下，通过了107次全对称循环，无任何裂纹形成。

图8 磁粉探伤检测

3.2 疲劳试验台

车轮疲劳试验验证采用轮轴全尺寸疲劳试验台进行，见图7。该试验台能够保证在车轮上施加旋转弯曲力矩并施加全对称应力循环。将车轮压装到试验轴[16]上，再将试验轮对垂直装在试验台的钢制凸台上。通过刚性夹持将车轮固定在钢制凸台上，确保试验轮对和试验台构架之间的刚性紧固。装在

试验结果表明，在车轮外侧应力最大位置及其附近区域的安全性能满足标准的要求，与基于有限元的疲劳计算结果一致。

4 结论

本文基于欧洲标准提出了一种车轮有限元模型的建立方法及车轮强度校核的方法。文中对有限元模型的建立方法及强度校核方法进行了详细的分析，结合车轮结构特点给出了High 形式Goodman单轴疲劳准则和Crossland 多轴疲劳准则对车轮进行了强度校核，从而得出车轮不同部位的安全系数。计算结果表明：实体车轮的静态安全系数和疲劳安全系数均满足标准的要求，且在车轮毂孔-辐板过渡区域安全系数最小。

按照标准推荐的试验方法[2]对该车轮的有限元计算结果进行了疲劳试验验证，在车轮安全系数最小的位置粘贴应变片，经过107次对称循环应力作用后，磁粉探伤检查未发现裂纹，从而验证了有限元计算结果的正确性。

本文对车轮安全性能的评估仅仅考虑了标准规定的4 种载荷工况，没有考虑实际路况下打滑、制动、温度等的影响。本文所述的有限元法评估车轮安全性能的方法可以为其他车轮安全性能的评估提供参考。