语法与语义接口理论的两条进路

陈鹏

语言伴随人类已经有数万年以上的历史了，然而人类对语言本质的了解还很初步。仅仅是在19 世纪，语言学还只不过是文献学或者人类学的一个分支，直到20 世纪，语言学才真正成为一门科学。

当学习一门语言的时候，我们通常会区分两部分的知识：一部分是词汇知识，另一部分是一般的语法知识。这种区分中似乎将词汇和句法进行了一个二分。

1 句法本位和词汇本位

也许，语言最为重要的一个秘密就隐藏在著名德国语言学家洪堡（W.von Humboldt）的论述中：“语言面对的是一个无穷无尽且真正无界限的领域，面对的是能被思考的万物本质。因此，它必须无限地使用有限方法，并通过产生语言和思想的标识能力来实现。”（[8],第91 页）对于洪堡的这段表述，后人一般都将其简述并抽象为对语言本质的一句概括，即：“语言是‘有限方法的无穷应用’”（language is the‘infinite use of finite means’）。语言中的语句集合显然是无穷的1当然，究竟语句集合是哪一类无穷？是可枚举的吗？这些问题都还存在争论。，然而生成语句的方法是有限的，几乎我们每一个人都能掌握这些有限的方法。要想研究语言，从这些有限的方法入手进行研究是比较有效的途径。

根据所理解的“有限方法（finite means）”的不同，语言学理论大致可以分野为句法主义和词汇主义。相较而言，句法主义（syntacticism）聚焦句法，更加侧重在短语结构构成的语法规则上。在句法主义的视域下，“有限方法”就是句法规则，乔姆斯基（N.Chomsky）用递归的形式文法体系揭示出“有限方法的无穷应用”的本质。相较而言，从词汇主义的立场来看，“有限方法”其实就是蕴藏于自然语言的“有限词汇”中，词汇主义（lexicalism）认为组合词汇的语法系统与组合短语的语法系统是独立的，语法信息根植于语言的词汇。产生词汇的组合系统应该与产生短语的组合系统应该具有不同的原则。正如兰贝克（J.Lambek）所言（[10]）：“一个被形式化的语言句子结构完全是由它的类型列表所决定的。”

句法主义的核心代表是乔姆斯基的转换生成语法，而词汇主义的发展相对分支较多，包括中心语驱动的短语结构语法（HSPG）、词汇功能语法（LFG）与组合范畴语法（CCG）等。

1.1 乔姆斯基的句法结构

乔姆斯基在《语言描写的三个模型》（[1]）、《句法结构》（[4]）、《有限状态语言》（[5]）、《论语法的某些形式特性》（[2]）和《语法的形式特性》（[3]）等系列论文和著作中，建立了形式语言理论的完整系统。

乔姆斯基在[2]中将形式文法描述为一个系统G，它是一个以有限符号集合V为其元素，以I为其单位元素集合的字符串接的半群，可记作：

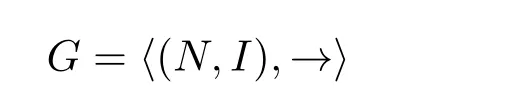
其中，V=VT ∪VN，VT表示终结符，VN表示非终结符（包含边界元素“#”），且VT与VN不相交。

→是在G上定义的一个二价关系，读作“可重写为”。该关系满足下面四个条件：

公理1→是非自反的；

公理2A ∈VN，当且仅当存在φ,ψ,ω，使得φAψ →φωψ；

公理3 不存在φ,ψ,ω，使得φ →ψ#ω；

公理4 存在有限偶对集合(χ1,ω1),...,(χn,ωn)，使得对于所有φ,ψ，φ →ψ

当且仅当存在φ1,φ2，且j ≤n，使得φ=φ1χφ2且ψ=φ1χφ2。

当实施以下约束后：

约束1 如果φ →ψ，那么存在A,φ1,φ2,ω，使得φ=φ1Aφ2,ψ=φ1ωφ2，且；

约束2 如果φ →ψ，那么存在A,φ1,φ2,ω，使得φ=φ1Aφ2，ψ=φ1ωφ2，且，但A →ω；

约束3 如果φ →ψ，那么存在A,φ1,φ2,ω,a,B，使得φ=φ1Aφ2，ψ=φ1ωφ2，且，A →ω，但ω=aB或者ω=a。

约束1 要求文法规则形如φ1Aφ2→φ1ωφ2，其中A是单个符号，。

约束2 要求文法规则形如A →ω，每个规则都可以独立于A出现的上下文。

约束3 要求文法规则限定在A →aB或者A →a，其中A和B是单个非终止符，a是单个终止符。

基于上述的形式化描述，乔姆斯基将语言的结构形式定义为四种类型。分别对应上述约束i，形成i型文法。即：满足约束1 的为1 型文法；满足约束2 的为2 型文法；满足约束3 的为3 型文法，此外没有约束的文法为0 型文法。相应的文法以及对应的语言、自动机参见表1。

表1:乔姆斯基的形式文法

在乔姆斯基的形式文法之后，语言的结构便可以按照不同的文法递归生成对应的不同的语言。这样的话，语言便形成一种螺纹状的层次结构，如图1 所示。

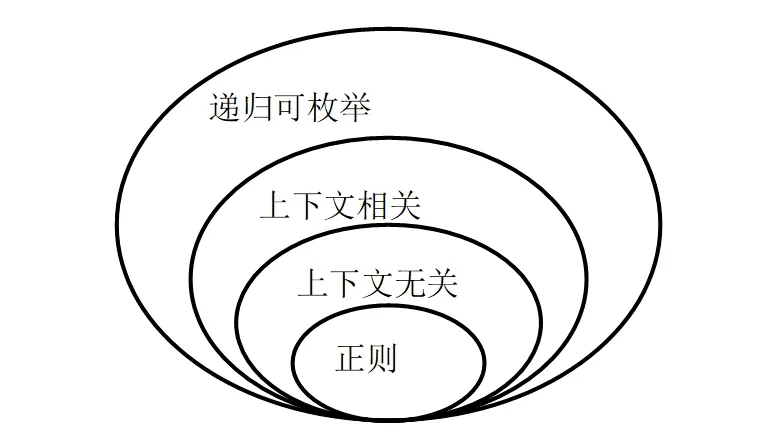
图1:基于乔姆斯基形式文法的语言层次结构

乔姆斯基眼中的语言世界是非常简洁而美好的，通过极其简练的几个句法规则，就可以产生如此丰富、美妙的语言。

1.2 组合范畴语法

与乔姆斯基的句法结构所不同，词汇主义的发展以词汇的形式化为核心，我们以组合范畴语法为例，展示词汇主义的核心思路。斯蒂德曼（M.Steedman）使用基于组合逻辑（[6]）的组合子规则的扩充古典范畴语法，创立了原生态CCG，旨在解决自然语言中大量存在却在上下文无关语法中不太容易得到解决的现象，如宾语提取、非外围抽象、词序灵活性、重成分NP–移位、动词毗连、主目毗连、直接成分的非连续性现象和多动词句、无界依存和寄生语缺（parastic gapping）等涉及到有界或者无界依存关系的自然语言表达式结构（[12,13]）。

CCG 主要由范畴和组合规则两部分构成。其中所有的词都指派一个对应的范畴，而范畴指的是它能够和什么样的论元组合以及与该论元组合之后会生成什么范畴，换言之，就是它的函数类型。词汇便成了从词汇条目到范畴的映射，意味着每个词汇条目寻求论元的行为。

范畴的集合是由一个原子范畴集合组合而成的：

定义1.给定一个有限的原子范畴类F，集合C是满足下列条件的最小集合：

a)F ∈C

b) 如果X,Y ∈C，那么X/Y,XY ∈C

例如，如果F={S,NP}，那么C的元素例中包括原子S和原子NP，以及(SNP) 和(NPNP)(NPNP)。由原子不断递归生成的对象被称为函子或复合范畴。

在任何一种复合范畴X/Y或XY中，我们将Y称为论元范畴，X为结果范畴；对任何X类来说，其修饰范畴的形式为X/X或XX，被修饰成分不做变化。在汉语中，词类如形容词和副词拥有修饰功能，这是因为形容词和副词分别修饰名词和动词，如：

(1) a.法规性⊢NP/NP；

b.然后⊢(SNP)/(SNP);

范畴声明它们的论元获取行为（argument-seeking），而组合规则作用于范畴之上使两个范畴依据其规定形成新的范畴。

组合规则给多个标记（token）赋予主要类型（principled types），并基于输入符号的范畴来限制组合的类型。由于组合规则与柯里（Curry）等（[6]）的组合子（combinators）之间紧密相关（close relationship），每个组合规则都有一个语义解释，这在语法分析过程中，允许语法派生同时构建谓词–论元结构（predicate-argument structure）。

表2:CCG 中范畴与语义规则

例(2)展现在组合范畴语法视域下，一个典型汉语语句的语句生成过程与范畴演算过程。

(2) 甘肃省积极探索高风险业务

此外，CCG 直观地体现了意义组合原则，其规则中语法与语义严格对应。CCG通常可以实现句法与语义并行推演，如例(3)所示。

(3) 张三吃了饭

2 语法与语义界面问题的源流与发展

语法与语义界面的问题与对语言结构的认识有着紧密的关系。在早期，人类对自然语言的理解是一体的，并不很严格地区分语法与语义。伴随着人类对语言的不断理解，语法与语义之间的界面不断显露且清晰。在乔姆斯基提出句法结构之前，语法与语义界面的问题并没有显露出来，也并没有作为一个严肃的科学主题受到过关注。在乔姆斯基的句法结构革命之后，语法与语义界面如同冰山一般逐渐露出了海平面。

乔姆斯基的《句法结构》之后，通过形式语法工具，将散落在盘子中的语言珍珠用形式语法这根金线串起来。通过语法的表层结构和深层结构的划分，似乎人类找到了理解语言的钥匙。基于转换生成语法，通过将否定和疑问语素加入到深层结构中，卡茨（J.Katz）和福多（J.Fodor）认为只需要通过深层结构便可以确定句子的意义。在1965年左右，人们普遍对卡茨–珀斯特假说持有乐观的态度，所谓的卡茨–珀斯特假说是“所有的转换都是意义保持的（meaning preserving）”（[9]，第23 页）。

卡茨–珀斯特假说让人类对语言的理解进入一个伊甸园时期，用简洁而美的句法形式就能勾画出如此丰富美妙的自然语言，无论是其形式或者其意义都完全在人类的掌握之中。

然而，很快地，量词辖域歧义问题就暴露出转换生成与语义之间的问题，并击破了卡茨–珀斯特假说。这里所谓的量词辖域歧义问题涵盖反身代词、等名消除（Equi-NP Deletion）和并列缩略（Conjunction Reduction）等不同情形，具体如例(4)至例(9)所示。

(4) a.张三投了自己一票。

b.张三投了张三一票。

(5) a.每个人都投了自己一票。

b.每个人都投了每个人一票。

例(4)表明反身代词的转换规则在应用到专名（“张三”）的情况下是意义保持的，然而当应用到例(5)量化名词短语（“每个人”）的时候却并不是意义保持的。

(6) a.张三想要获胜。

b.张三想要张三获胜。

(7) a.每个人都想要获胜。

b.每个人都想要每个人获胜。

例(6)表明对于专名而言，等名消除的转换规则应用后，意义保持不变，然而在例(7)中等名消除的转换规则应用到量化名词短语时意义却发生变化。

(8) a.3 既是偶数又是奇数。

b.3 是偶数，并且3 是奇数。

(9) a.没有数既是偶数又是奇数。

b.没有数是偶数，并且没有数是奇数。

例(8)和例(9)同样都是并列缩略的转换规则，但作用对于专名和量化名词短语所表现出来的意义保持却不相同。例(8)在并列缩略的转换规则下是意义保持的，而例(9)在并列缩略的转换规则下意义却发生变化。

例(4)至例(9)所展现的问题核心是转换生成与语义之间的问题，语义的问题已经不能完全由深层结构所确定。这个时候，原本在卡茨–珀斯特假说中明晰的语法–语义界面又变得模糊起来了。由于这个问题，引发了语言学史上著名的一场语言学战争（[7]），其中一派是生成语义学派，另一派是解释语义学派。战争的结果并不是一派战胜另一派，而只是将人类从由卡茨–珀斯特假说所构筑的语言伊甸园中驱逐出来。人类又一次被语法与语义之间模糊而难以琢磨的关系所困扰。

蒙太格语法使得人类又一次重新认识语言，相比于乔姆斯基的句法结构革命，这一次的认识转向对语义有了一个全新的认知。蒙太格提出语法实际上是一种“形式”的代数，语义是一种“意义”的代数，且在句法代数和语义代数之间存在着一种同构关系。这种语言观重塑了语法与语义的界面。

此外，蒙太格语法对与语法与语义界面研究的最主要的贡献是技术层面的。蒙太格语法对于语法与语义的界面提供了两个至关重要的技术工具，一是Lambda 演算，另一是将内涵视为弗雷格的高阶函项。

在蒙太格语法之前，通常采用一阶逻辑来描述自然语言。然而，一阶逻辑的表达能力与自然语言相比实在是差距甚远。通常，我们使用一阶逻辑与自然语言的照应如表3 所示。一阶逻辑通常主要能够刻画一般的动词、通用名词、形容词、专名等，然而对于限定词、量词、介词、副词以及相关的一些短语，一阶逻辑都不能很好地进行刻画。

然而，当有了Lambda 演算和高阶函项，刻画自然语言的方法丰富了很多。Lambda 演算为函项表示提供了重要的基础，在以往的函项中，有一些复杂语句是不能给出其组合语义的。

通过Lambda 演算，可以在不依赖于论元的前提下，提供指称函项的一种方法，因此可用于为类似量化限定词设计合理的语义。以例(7)为例，我们可将“每个”翻译为一个二阶函项，并通过与“人”这个通用名词组合产生广义量词指称。Lambda 演算为分析复杂表达式的意义提供了方法，明确了一个从自然语言语法到语义翻译的组合式过程，为语法树的每一个节点都指派一个合适的意义。

(10) 每个人都在读书

蒙太格语法无疑是里程碑式的，其影响也极为深远。实际上，蒙太格语法并没有完全地实现蒙太格为形式语言和自然语言构筑一个通用文法的梦想，然而它却对逻辑学，尤其是数理逻辑和语言学的融合起到了奠基性的作用。2在蒙太格语法之后，国际上逐步形成了一门名为“形式语义学”的逻辑与语言的交叉学科。对于语法与语义界面的问题，蒙太格语法也并没有给出最终的答案，然而它将语法和语义分别视为两个自治的系统，且彼此存在着紧密关联（同构）的这一观点为后人对待语法与语义提供了非常关键的启示。虽然语法与语义界面的问题犹如荆棘一般，仍布满在人类通往语言理解的路途中，然而人类手上已经持有数理逻辑的利刃，一路披荆斩棘。

在蒙太格语法之后，如果我们认为语法和语义都是自洽的，那么语法与语义的界面问题突出地表现在语法与语义的不匹配。而语法与语义的界面理论本质上都是对这些不匹配的消解方法。比较常见的语法与语义界面的现象包括：论元识别、量化、歧义等。

(i)论元识别问题

在一般情形下，在语态和逻辑语义词汇之间存在一个非常清晰的照应：我们可以将一个专有名词翻译或者解释为一个个体，将带有一个主体和n个补语的动词翻译或者解释为带有n+1 个论元的谓词。例如：

(11) a.张三喜欢王芳。

b.喜欢(张三,王芳)

句法结构与语义结构非常不同。即使我们能够标识出词与其意义之间的映射，我们知道整个语句的真值条件，我们仍然没有谓词–逻辑公式的子表达式，照应动词短语节点的意义。语法与语义的界面需要确保直接宾语的指称与谓词“喜欢”的第二个语义论元槽关联，同时主语指称必须与第一个论元槽相关联。

论元标识的另一个问题是当谓词的语义元并不对应句法价。例如：

(12) a.张三看上去很疲惫。

b.看上去(很疲惫(张三))

从表层而言，张三是看上去的主语，然而张三又不是谓词看上去的语义论元。

(ii)量化问题

一般情形下，动词的句法依存成分被翻译为动词的语义论元。然而，当依存成分是量化的，例如：

(13) 每个人都在读书。

a.For all(reading)

b.∀x[man(x)→reading(x)]

其中，动词的翻译被视为主语的语义论元。因此我们可以假设“每个人”翻译为高阶谓词For all，它将一个一阶谓词“reading”作为其论元。在(10b)这个标准的谓词逻辑翻译中，主语的语义贡献分散在整个表达式中。然而，主语的一部分被视为“reading”的论元，同时reading(x)这一公式却处于量化词∀的辖域中。

(iii)辖域歧义

在自然语言中，歧义现象是比较普遍的。我们以辖域歧义为例：

(14) 每个学生都在编写某个程序。

a.∀x(λx.student(x)→∃y(λy.(program(y)∧wrote(x,y)))

b.∃x(λx.program(x)∧∀y(λy.student(y)→wrote(y,x)))

例(14)是一个非常典型的量词辖域问题。对于同样一句话，由于量词所采用的辖域宽窄不同就产生了不同的解读。(11a)中“每个学生”中的“每个”采取了宽辖域，而“某个程序”中的“某个”处于“每个”的辖域范围内。这样的解读表明每个学生可能都在编写完全不同的程序。(11b)中“某个程序”中的“某个”采取了宽辖域，而“每个学生”中的“每个”处于“某个”的辖域范围内。这样的解读表明所有学生都在编写同一个程序（比方说求100 的阶乘）。

量词辖域歧义问题是语法与语义界面中普遍存在的一个重要现象，我们还可以列举一些相关的例子。

(15) a.大多数语言学家会讲两种语言。

b.所有男生都喜欢某个篮球运动员。

c.所有程序员都会用一种程序语言进行编程。

3 语法与语义界面的两条进路

任何的语法与语义界面理论都是一种将语法分析与语义分析关联的理论。在乔姆斯基和蒙太格的工作后，对于语法与语义界面的研究蓬勃发展。然而，总体而言，在语法与语义界面的理论有两条比较主要的进路，一条是以词汇为中心的词汇主义路线，另一条是以句法为中心的句法主义路线。

词汇主义路线的代表是范畴语法，最初的范畴语法可以追溯到AB 演算，在兰贝克那里得到比较完善的形式化描述。莫特盖特（M.Moortgat）对范畴语法的语法与语义界面观做过总结：

范畴类型逻辑对于形式与语义之间的关系给出一个高度透明的观点：语义解释能够直接通过证明获取，同时证明也构建了表达式的良型（可生成）。组合性原则以一种特别严格、纯粹演绎的形式实现，没有为规则到规则所规定的意义指派遗留任何空间。（[11]，第115 页）

句法主义路线的代表是乔姆斯基学派的转换生成语法以及逻辑形式（Logic Form，简称“LF”）。在LF 方法中，句法被视为句法表征集合，从D结构出发，被映射为S结构，然后再被同时映射为音素形式（Phonological Form）和LF。这些表征是句法树。这种语法–语义界面观点给我们提供一个明确的界面层次以及理论假设，它们可以通过句子的S结构产生。理想情况下，从S结构到LF 的映射操作与从D结构到S结构所需要的操作非常相似。

LF 具有一个模型论解释。可以假定一个语句的LF 能够直接通过一个相对简单的组合性假设来解释：词项元素的解释在词库中给出，短语节点的解释是对其直接孩子节点的解释的组合结果，其中组合通常是采用函项应用，但也允许一些其他的操作。

句法主义路线在语义方面，通常假定某种版本的蒙太格内涵逻辑，例如加林（D.Gallin）所开发的版本。通常将词解释为复杂函数，使用Lambda 项来陈述。由于采取的具体LF 形式不同，句法主义也存在很多的类型，然而整体上而言，句法主义相较于词汇主义的不同有两点：一是句法主义普遍允许在句法层次有更多的抽象；另一点是句法主义倾向于在句法生成的过程中消解语法与语义的不匹配。

我们以量词辖域歧义的消解为例，来阐释词汇主义与句法主义在处理语法与语义界面问题中的异同点。例(16)是一个非常典型的量词辖域的歧义句。句法主义方法主要采用量词提升的方法，而词汇主义方法采用的是丰富词库和语义本体的方法。

(16) 每个学生阅读某篇论文。

(i)句法主义方法

在透明LF 方面中，QR可以将宾语量化词置于主语量化词的辖域内或者辖域外，产生两个消岐的LFs，这两个LFs 反过来产生两个真值条件完全不同的解释：

(17) a.LF1：[每个学生λ1[某篇论文λ2[t1阅读t2]]]

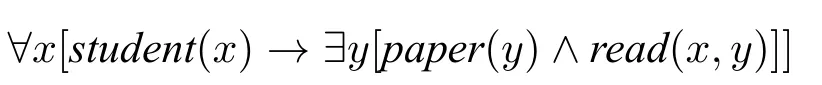
b.LF2:[某篇论文λ2[每个学生λ1[t1阅读t2]]]

LF 分析为量化表达式产生所谓的前束范式，其中所有的量化词出现在包含他们所约束变元的开放公式的前面。

(ii)词汇主义的方法

在词汇主义路线中，以CCG 为例，在对待(16)这样的歧义消解采用丰富词汇和语义本体的方法。我们对此采用CCG 方法进行歧义消解的尝试。

(18) 每个:=(T/(TNP))/(T/NP):λP.λQ.∀x.(P(x)→Q(x))

每个:=(T(T/NP))/(T/NP):λP.λQ.∀x.(P(x)→Q(x))

(19) 某篇:=(T/(TNP))/(T/NP):λP.λQ.∃x.(P(x)∧Q(x))

某篇:=(T(T/NP))/(T/NP):λP.λQ.∃x.(P(x)∧Q(x))

其中T是一个范畴变量，可以取值S。

经过类型提升，我们就可以并行地推演例(16)中的语句。

根据上述例子，我们可以发现CCG 在处理量词辖域主要是在范畴指派上进行灵活应对，通过词条的不同范畴指派最终推演出表现辖域歧义的两个语义解读。

处理语法与语义的不匹配问题是语法与语义界面理论的核心，句法主义和词汇主义的两条不同进路代表着对待语法与语义界面的两个不同方向。句法主义的进路偏重语法，将语义视为语法的一个影子，在遇到语法与语义的不匹配情形时，句法主义期望抽象语法，同时在句法生成过程中去解决不匹配问题。词汇主义相对更平等地对待语法和语义，在遇到语法与语义的不匹配的情形时，词汇主义期望通过丰富词汇或者语义本体来解决不匹配问题。