基于神经网络的复杂导弹系统可靠性预测*

苏续军，吕学志，方 丹，陈 晓

（1.陆军工程大学石家庄校区，石家庄 050003；2.解放军32179 部队，北京 100012）

0 引言

系统可靠性表示系统在规定的条件下和规定的时间内完成规定功能的能力［1］。目前，系统的可靠性建模与分析方法大致可分为组合模型法、随机过程法、系统仿真法和通用生成函数法4 类：

1）组合模型法。它是基于系统和部件之间功能逻辑关系的一种分析方法。在进行建模之前，需要对系统进行功能和结构分解，从而建立系统和部件之间清晰的功能逻辑关系，主要包括可靠性框图法、故障树分析法（Fault Tree Analysis，FTA）、故障模式影响与危害性分析法（Failure Modes Effect and Criticality Analysis，FMECA）［1］。

2）随机过程法。主要是指建立马尔可夫模型。马尔可夫模型是指马尔可夫链（Markov Chain）模型，主要用来分析系统处于各个可能状态的概率。由于马尔科夫过程方法要求系统各状态的驻留时间必须服从指数分布，且当部件数量或部件状态较多时计算十分繁杂，使得其在工程中的应用受到很大限制［1］。

3）系统仿真法。当系统各个阶段的单元相关性较复杂，或者系统可靠性、维修性分布不是指数分布时，应用上述方法较为困难，只能应用系统仿真法。仿真方法理论基础是概率论中的基本定律——大数定理，这一方法的优点是可以适用于任何情况，主要困难是仿真计算工作量大，计算精度难以保证［2］。

4）通用生成函数法。Ushakov［3］在上个世纪80年代对生成函数进行了扩展，提出了通用生成函数的概念，后来Levitin 和Lisnianski［4］等在多态系统可靠性领域引入通用生成函数方法，随后该方法在多态系统可靠性分析与优化设计中得到了广泛应用。通用生成函数方法能够清晰地表达系统的结构函数及部件之间的功能逻辑关系，面对不确定逻辑关系则受到其表达方式的限制。由于其形式比较简单也统一，表达简洁，通用性强，所以运用比较广泛，但是同时也存在计算量大等缺点。它主要用来解决确定性的结构函数和功能逻辑的多态系统可靠性分析及优化的问题。

随着科技的发展，武器装备日益复杂，对可靠性分析的要求也越来越高。由于传统可靠性分析理论的局限性，其很难满足实际的需要。由于神经网络具有强大的非线性映射能力和高效的泛化能力，而且建模框架通用性好，因此，在可靠性工程中得到了越来越多的应用，越来越表现出相对传统可靠性理论的优势。文献［5］利用发动机部件实验中的故障数据通过神经网络对其可靠性进行预测。文献［6］介绍了如何通过神经网络，利用汽车设计阶段可靠性数据来预测其使用阶段的可靠性数据。文献［7］基于BP 神经网络理论，提出分析某型潜艇的人-艇-环境系统可靠性的方法。文献［8］综合使用神经网络和决策树对洗衣机的可靠性进行了预测。文献［9］运用神经网络和遗传算法对飞机故障次数进行了预测。文献［10-11］针对软件可靠性，分别给出了基于循环神经网络和前馈神经网络的建模方法。文献［12-13］还将神经网络应用于解决可靠性分配与优化问题。

上述用于可靠性建模与分析的神经网络都是浅层的神经网络，而新兴的深度学习网络是原有神经网络的进一步发展，具有更强大的映射能力、泛化能力，适应性和鲁棒性更好。目前，有必要将这种技术用于复杂系统可靠性建模与分析问题。为此，本文对该问题进行展开研究。

1 问题描述

本文的研究对象是某型导弹，研究的目的是找到通过导弹的测试和飞行可靠性的历史数据，来预测导弹未来可靠性的方法。

导弹的维修方案不适合连续收集导弹状态数据。导弹通常储存在安全的、加固的发射筒（或容器）中，以免受外界不良因素影响。但是，导弹被定期地从发射筒取出，进行维护、测试、训练、作战。因此，通过导弹测试可以获取大量数据，导弹测试数据从某种程度上与导弹可靠性存在一定关联。表1给出了导弹测试类型和描述。下页图1、图2 说明了各种测试的相关关系。

此外，导弹飞行可靠性数据是可以获得的。这些数据来自每年的靶场实验、训练和演习记录。

表1 测试类型及描述

图1 接口测试

图2 惯性制导自动校正相关测试

为了获得模型的有效输出，必须使用有效的目标。具体来说，该模型将尝试使用地面测试数据来近似年度飞行可靠度。飞行可靠度的时间（年度）序列构成了“目标向量”。导弹采用冷发射（外力发射），即依靠外力将导弹弹出发射筒到达一定高度后，导弹自身的发动机点火继续飞行。飞行阶段分为3 个阶段：弹射阶段、自飞行阶段和末段打击阶段。弹射阶段开始于导弹与发射筒分离，并在导弹自身发动机点火后结束。巡航阶段开始于自身发动机点火，并在末段打击之前结束。末段打击从战斗部机动开始，并以导弹爆炸结束。下页图3 给出了典型任务的事件序列。

每枚飞行的导弹使用遥测套件向地面站发送导弹状态信息，可以容易地识别发生故障的任务阶段，以及故障原因。导弹飞行可靠度计算公式如下：

其中，R 为导弹可靠度；RT为弹射的可靠度；Rc为导弹巡航的可靠度；RE为末段打击可靠度。

2 建模思路和方法框架

2.1 建模思路

图3 导弹任务序列

根据导弹测试数据与导弹飞行可靠度的关联性，以及导弹测试数据和导弹飞行可靠度的时间序列关联性，利用基于序列机制的神经网络来预测导弹飞行可靠性。从直觉上讲，导弹测试通过率高，导弹飞行可靠度就会高；反之，则导弹飞行可靠度会低。按照时间先后顺序，导弹测试结果和导弹飞行可靠度组成一组时间序列，这一事件序列从某种程度上具有某种时间序列关联性。该问题很难用线性模型进行描述，而神经网络适合对这种非线性的关联关系以及时间序列关联性进行建模，大大降低了模型建立的难度和工作量。只需将神经网络看成是一个黑箱子，根据输入与输出数据，神经网络依据相关的学习规则，便可以建立相应的数据模型。

2.2 方法框架

复杂系统可靠性预测方法包括以下步骤，如图4 所示。1）数据预处理。收集可靠性相关数据，根据经验去除冗余的数据项，补充缺失数据，对原始数据进行一定处理。2）特征选取。利用数理统计分析技术进一步去除冗余的数据项，达到降维的目的。3）建立深度学习网络模型。利用复杂系统可靠性数据分别构建基于RNN、LSTM、GRU 的可靠性预测模型。4）数据融合。融合RNN、LSTM、GRU 模型的输出结果，以得到更合理的结果。

图4 复杂系统可靠性预测框架

3 数据预处理

使用下面简单的公式，将测试结果标准化为通过率：

用1 级B 型测试结果（故障验证测试）对MIT和SIT 的合格率进行了假阴性调整。通过B 型测试的导弹按照正在进行测试的导弹数量的比例记入MIT 和SIT 通过率。

然后，需要确定时间序列的周期（是选择月，还是年）。时间序列周期的确定需要考虑数据的连续性。数据分析表明，MIT 主要运行在演习和飞机出动过程中，即它们不是每个月都有。使用每月平均值将导致有些月份测试结果是空白，显然这是不合适的。当然，导弹未通过MIT 将重新进行1 级B 型测试来验证失效。在某些情况下，1 级B 型测试与MIT不在同一月份中，将在下个月进行。在这种情况下，对MIT 通过率的B 类修正不会记入适当的月份。而在年底统计上述测试结果会避免上述问题。最后，装备管理部门通常使用年度数据而不是月数据来进行规划。

4 特征选择

在真实世界中，工程问题通常具有非线性的特点。神经网络适合于对非线性问题进行建模。一般可以将神经网络看作“黑箱”，只要将输入、输出数据集交给神经网络进行学习训练，就会得到描述输入、输出复杂关系的神经网络模型。然而，如果数据集自变量较多、自变量之间存在相关性的话，则可能会有“过拟合”问题，因此，会降低模型精度、延长训练时间。所以，当建模之前，必须对数据集的特征进行选择，去掉冗余的、相关的变量，保留体现输入和输出数据真实关系的变量。近年来，许多人对变量压缩降维问题进行了深入研究，取得了一定的成果。常用的变量压缩方法有多元回归与相关分析法、类逐步回归法、主成分分析法、独立成分分析法、主基底分析法、偏最小二乘法、遗传算法等［14-16］。本文主要使用因子分析。

因子分析（factor analysis）模型是主成分分析的推广。它也是利用降维的思想，由研究原始变量相关矩阵内部的依赖关系出发，把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。相对于主成分分析，因子更倾向于描述原始变量之间的相关关系，如下页图5 所示。

图5 因子分析的逻辑框图

5 神经网络模型

5.1 循环神经网络

在前馈神经网络（Forward Neural Networks，FNN）［17］中，每层神经元将上一层神经元的输出作为输入，神经元信息传播是单项的，自身并不在反馈连接，因此，FNN 只能建立当前输入与输出之间的对应关系，通常用来处理相对简单的静态特征。但在处理具有时序特征的数据时存在很多的局限性，循环神经网络（RNN）有别于传统的FNN，旨在通过建立神经元的自反馈连接，建立全部历史输入信息与当前输出的对应关系，实现对时序特征的记忆功能，进而提升网络的分类能力。RNN 网络拓扑结构如图6 所示。

图6 按时间展开的循环神经网络模型

展开的RNN 模型可以看作一个深层网络，该深层网络的每一层对应一个时间步，各层之间共享权值（如图中的U、V 和W）。因而，可以使用随时间反向传播算法（Back Propagation Through Time，BPTT）对RNN 在多个时间步上进行训练。

RNN 的前馈传播过程与FNN 基本相同，不同的是隐含层输出输入由两部分组成，即当前的输入信息和上一时刻隐含层的输出信息。假设输入层有I 个节点，隐含层有H 个节点，输出层有K 个节点，网络的各层输入输出由公式给出。

其中，U、W、V 分别为输入层到隐含层、隐含层到隐含层、隐含层到输出层的网络权值（网络偏置值作为权值的一部分统一计算，这里不再单独表示），输入为长度T 的序列X，X（t）为t 时刻的输入值，a（t）为t 时刻隐含层的输入值，H（t）为t 时刻隐含层的输出值，o（t）为t 时刻隐含层的输出，f、θ 分别为隐含层与输出层的激活函数。

5.2 长短时记忆网络

RNN 虽然在一定程度具有了对时序特征的学习能力，但在学习过程中容易先梯度消失或梯度爆炸的情况，误差的反向传播不能回传到足够远的时间步上，导致RNN 无法学习到远距离时间步上的特征对当前输出的影响，也就是“长期依赖”问题。1997 年Sepp Hochreiter 和Jurgen Schmidhuber 提出了长短时记忆网络（LSTM）模型，该模型有效地解决了RNN 存在的上述问题［17］。在这个模型中，常规的神经元被记忆单元所代替。每个记忆单元由一个输入门，一个输出门和遗忘门组成。LSTM 记忆单元模型如图7 所示，Cell 单元被称为“细胞”，细胞状态存储了当前网络对以往时间步特征的记忆信息；输入门可以判别当前输入是否重要；输出门可以从隐层状态分离最终的记忆，可以评估细胞状态S（t）哪一部分需要显示在隐层状态h（t）中；遗忘门用于决定丢弃细胞状态中的某些信息，它读取x（t）和h（t-1），输出0 或1 并传递给细胞状态，“0”代表丢弃，“1”代表保留，从而更改系统状态为。

图7 LSTM 记忆单元模型

首先，利用网络在t 时刻的输入x（t）和t-1 时刻隐含层的状态h （t-1），计算各输入节点的值，如式（12）所示：

然后，计算所有单元输入门的值如式（13）所示：

同样，计算所有单元遗忘门的值，如式（14）所示：

计算所有单元输出门的值，如式（15）所示：

计算并更新模型在t 时刻的状态，如式（16）所示：

最后，计算并更新模型在r 时刻的输出，如式（17）所示：

其中，σ 表示Sigmoid 函数，σ（z）=1/（1+e-z）；φ（z）=（ez- e-z）/（ez+ e-z）。

5.3 门限循环网络

门限循环网络模型（GRU）是长短时记忆网络的一种变体，其原理基本相同，结合遗忘门与输入门主要功能设置更新门［17］。

计算记忆单元的输出h（t）由式（21）所示：

其中，σ 表示Sigmoid 函数；φ 表示Tanh 函数。

图8 GRU 记忆单元模型

5.4 数据融合方法

当从3 种深度学习网络（RNN、LSTM、GRU）得到输出结果后，还需要融合3 种不同结果，这就需要一种融合输出结果的方法。理想地讲，与任何单个网络输出相比，融合后的输出结果可以减小均方误差。模型中的每种深度学习网络都是不同的，这是因为网络的初始权重是随机生成，这就使得训练的起始位置不同，此外神经网络结构也是不同的。这些因素再加上梯度搜索方法可能导致每种网络在错误空间中找到不同局部最小值。局部最小值是重要的，因为它们反应了在整个数据域中不同网络的性能。因此，当融合不同网络输出结果时，会得到更多信息，模型的性能会提高。用于融合不同网络输出简单有效的方法被称为通用融合方法（Generalized Ensemble Method，GEM）。通用融合法需要组合N 个网络的输出结果，第i 种网络的输出结果为fi（x），融合后的结果为

其中，αi必须满足约束∑αi=1；mi被定义为网络fi（x）与未知函数f（x）的差。文献［18］定义一个相关矩阵Cij（E［mi（x）mj（x）］），提出通过最小化∑ijαiαjCij以实现MSE［fGEM］的最小化，并认为当下式成立时，

将实现MSE（均方误差）的最小化。简单地说，通过不同网络之间的相关矩阵可以得到相应网络的输出“权重”。只要将每种网络的输出结果加权求和就能得到一种新模型，并且会减小了整个模型的MSE。这个结果来自不同网络捕获的错误空间的不同部分，但是组合网络可以捕获比任何单个模型更多的错误空间。

6 示例

在建立用于预测导弹飞行可靠性的神经网络模型时，必须从地面测试数据库中选择相关特征。根据定义，B 类测试仅发生在A 类测试提示导弹故障之后。因此，模型中并不包括LLT B、Level Ⅰ-B、Level Ⅲ-B。其他的测试包括A 类发射测试（LLT/LPT Type A）、系统接口测试（SIT）、导弹接口测试（MIT）、A 类1 级测试（Level 1 Type A）和惯性导航组件自动校准（INE Auto-cal）。按照第3 节中数据预处理方法对导弹测试数据和可靠性数据进行预处理，得到导弹年度测试数据和可靠性数据，如表1 所示。

本文使用了因子分析方法对数据特征进行了选择。在具体实现过程中，可以利用Matlab 中的factoran 函数对表1 数据进行因子分析。因子分析结果如表2 所示，从中可知4 个因子即可以解释数据集90%以上的总方差。载荷因子经过最大正交旋转（Varimax）之后特征的载荷如表3 所示。Varimax 可以说是最常见的正交旋转方法，它重新旋转了初始载荷的坐标轴（同时保持点的相对位置）以最大化变量因素载荷的方差。表3 清晰描述了构成数据集中各因素之间的关系。对因子1 来说，对其影响最大的是惯性导航组件自动校准和A 类1 级测试；对因子2 来说，对其影响最大的是A 类发射测试；对因子3 来说，对其影响最大的是导弹接口测试；对因子4 来说，对其影响最大的是系统接口测试。通过综合计算，系统接口测试影响较小，最终将系统接口测试剔除。

用2007 年-2017 年导弹数据作为3 种神经网络的训练数据。使用每3 年数据作为输入向量，第4年数据作为目标向量。RNN 网络、LSTM 网络、GRU网络输入结点均为15，输出结点均为5 个，隐藏结点均为20 个。每种网络经过3 000 此训练，每个年度输出结果如表5 所示。输出结果和目标可靠度的差如下页表6 所示。由于Cij=E［mi（x）mj（x）］，可以利用统计的方法得到相关矩阵，如表7 所示。根据式（22）可以得到α1=0.296 7，α2=0.269 4，α3=0.433 9。最终利用神经网络模型，以及2015-2017 年度测试数据和可靠性数据可以预测2018 年度导弹可靠度为0.876 2。

表1 导弹测试数据库

表2 因子分析结果

表3 旋转后的因子载荷

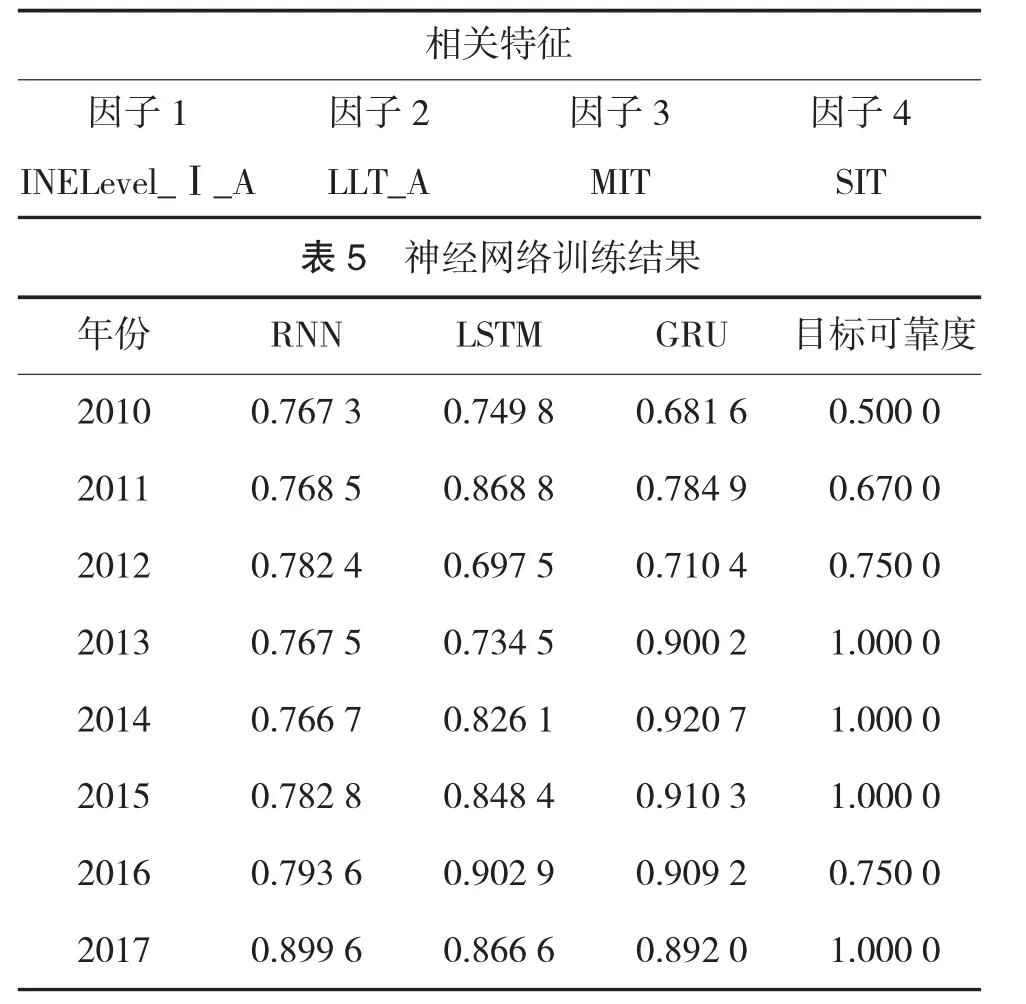
表4 因子分析分类

表6 输出与目标可靠度的差

表7 相关矩阵

图9 可靠性预测结果

7 结论

本文介绍了如何利用神经网络对复杂导弹系统可靠性进行预测。对利用导弹地面测试数据和可靠性数据预测未来导弹可靠性问题进行了描述。给出了建模思路和方法框架。探讨了基于因子分析的可靠性数据特征选择方法、循环神经网络（RNN）、长短时记忆网络（LSTM）、门循环网络（GRU）以及输出数据融合方法。最后，在实例中利用本文提出的方法对导弹可靠性进行了预测，验证了方法的可行性与有效性。该方法可以充分利用复杂系统地面测试数据、可靠性数据中隐含的信息以及多种神经网络的优点，具有一定的通用性与实用性。