多站遥测数据加权融合方法

杨军佳

（陆军炮兵防空兵学院郑州校区，郑州 450000）

0 引言

在靶场导弹飞行试验中，遥测数据处理任务就是将各遥测测量站的数据按一定要求和方法进行计算分析，最终将原始数据还原成各种物理量，为靶场各型导弹的性能评估和故障诊断提供主要依据［1］。为了得到比较全面且精确的导弹数据，往往利用靶场中的多部遥测设备进行同时测量，而后对遥测数据进行融合处理。关于数据融合的方法非常多，相比于贝叶斯决策以及神经网络等融合技术，在实际运用中主观随意性比较大以及建模的局限性，加权融合方法以其无需先验信息且融合精度比较高的优势得到广泛关注。文献［1］将分批估计算法应用于遥测数据融合处理，取得了较好的遥测数据融合效果；文献［2］针对未知传感器测量精度的多传感器时间控制系统，提出了依据实测数据之间的相互关系确定数据加权融合过程中的权值分配问题，通过仿真证明了算法鲁棒性强、融合精度高以及计算量小的优点；文献［3］针对未知测量精度的多传感器数据融合问题，通过对测量值的模糊处理、时间序列上融合值与测量值的相互转换以及信噪比概念的引入，确定数据融合过程中的权重分配，并通过仿真验证了算法的精确性、稳健性以及计算简单的优点；文献［4］针对复杂环境下多传感器数据融合问题，构造了正弦以及反正弦两种支持度函数，依据信噪比的概念构建一致性均值和可靠性测度的权重分配模型，并通过仿真验证了两种支持度函数的有效性；文献［5］针对多无线传感器监测数据融合精度低的问题，提出首先采用分批估计的方法确定单传感器的最优估计值，而后依据权值最优分配原理进行多传感器监测数据的融合，并通过实测数据验证了算法融合精度性以及稳健性的优点；文献［6］针对多传感器数据融合问题，将证据理论中的修正证据距离引入传感器测量数据间相互关系的计算，并以此确定数据融合权值分配，仿真结果验证了算法融合效果较好以及鲁棒性较强的优点；文献［7］针对雷达航迹融合问题，提出将固定权值改进为动态权值的融合方法，将数据融合的权值分为动态和静态两个部分，其中静态部分取决于各传感器的分辨率信息，动态部分取决于传感器测量值和数理统计以及卡尔曼滤波之后的基准值。文献［8］采用模糊贴近度作为数据加权融合的权重，并对倒数型距离贴近度进行修正，以此提高加权融合算法的精度和可靠性。文献［9］针对数据融合时权重难以确定的问题，提出基于模糊熵的加权融合算法。文献［10］针对多源数据融合问题，提出了采用信息熵对自适应加权融合估计进行改进，并利用优化算法确定数据融合权重。文献［11］将证据理论中的修正距离引入传感器数据之间距离的计算，分别讨论了传感器精度已知或者能够计算，以及传感器未知且无法计算的两种情况的数据融合。文献［12］为提高无线传感网络监测系统的可靠性及寿命，提出了基于分簇的自适应预测加权数据融合算法。以上文献所提加权融合方法虽然都取得了比较不错的融合效果，但融合权重的确定要么取决于传感器标称的测量精度，要么仅仅依靠传感器测量数据间的相互关系。而传感器测量精度可能会受到周围环境的干扰，依靠传感器间测量数据相互关系确定的融合权重，明显不符合加权融合最优权值分配原则。本文以最优权值分配原则为基础，通过对遥测设备实测数据的统计分析，计算遥测设备实际测量精度，进而对遥测数据进行加权融合，较好地解决了上述文献中所提加权融合方法的不足之处。

1 问题描述

假设某靶场内部署的N 部遥测地面站设备分别对试验中的某型导弹进行测量，ai（p）为第i（1≤i≤N）部遥测设备对导弹某参数p 时刻的测量值，且测量误差为εi（p），则第i 部遥测设备对导弹某参数的测量方程可表示为：

图1 遥测设备与导弹位置示意图

2 理论分析

2.1 遥测设备融合权重分析

如果在N 部遥测设备数据融合的过程中，第i部遥测设备的权值为ωi，则融合结果为：

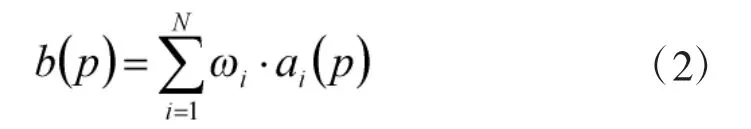
式中，b（k）表示p 时刻N 部遥测设备数据融合结果，ai（p）表示第i 部遥测设备p 时刻的测量值。

根据文献［13-15］中最优权值的研究，当第i 部遥测设备的融合权值满足下式时，融合结果的精度最高：

从式（3）可以看出，在最优权值分配的情况下，融合权值只与遥测设备的测量精度有关。然而，限于遥测设备本身稳定性，以及在对导弹进行测量的过程中可能受到来自周围环境的干扰，遥测设备标称的测量精度并不能直接用于数据融合过程中权重值的计算。

2.2 遥测设备测量精度分析

由式（1）可知，p 时刻第i 部遥测设备与第j（j≠i）部遥测设备对导弹某参数的测量值存在以下关系：

由上式可得：

令第i 部遥测设备对导弹某参数的M 次测量值记为Ai，对应的测量误差记为Δi，则可得：

对式（6）两侧求方差可得：

式（7）中，在已知遥测设备M 次测量值的情况下，等式左侧为一常数，记为。

则式（7）可记为：

第i 部与第j（j≠i）部遥测设备两部之间的量测噪声方差满足式（8）中的关系，则N 部遥测设备之间量测噪声方差可构建个方程，其中待求参数为N 个，即：

当N=2 时，E=［1，1］，两部遥测设备量测噪声方差之和为一常数，此时的解不唯一。即，当N=2 时，不能求解出遥测设备的量测噪声方差。精度。

3 数据加权融合方法

假设各遥测设备对导弹的测量数据在时间历程上已实现匹配对准。该方法的具体步骤如下：

步骤1：遥测设备实时测量精度的计算

按照上述理论分析的第2 部分，对于不同遥测设备探测的目标参数，依据式（9）计算遥测设备实际的参数测量精度。

步骤2：不同遥测设备融合权重的确定

按照上述理论分析的第1 部分，依据式（3）计算不同遥测设备参与数据融合的最优权重。

步骤3：不同遥测设备探测数据的加权融合

按照上述理论分析的第1 部分，依据式（2）计算不同遥测设备数据的融合结果。

4 仿真分析

表1 不同采样时刻导弹飞行高度真实值

为便于检验融合效果，参考标准差的概念定义融合精度为：

式中，σ 表示融合精度，M 表示采样时间，h（p）表示第p 个采样时刻的融合数据。

为便于对比分析，本文将利用传感器标称测量精度确定融合权重的最小二乘加权融合算法定义为算法1，将文献［6］中利用传感器间测量数据相互关系确定融合权重的加权融合算法定义为算法2。3种算法进行100 次仿真的融合效果如图2 所示。

图2 不同算法融合效果对比1

从图2 可以看出，3 种算法的融合效果变化趋势基本一致，但本文算法的融合效果优于算法2，稍逊于算法1。其中，算法1 和本文算法的融合精度基本在0.8 m 左右，该数值小于任何一部遥测设备的测量精度；算法2 的融合精度基本在1.1 m 左右，略大于测量精度最高的遥测设备。

导致上述结果的主要原因是不同算法数据融合过程中权重的分配。为便于直观地理解权值分配对不同算法融合效果的影响，本文分别与算法1 和算法2 进行对比分析。

4.1 与算法1 的对比分析

4.1.1 融合权值合理性分析

为检验两种算法权重确定的合理性，将表1 中样本数据进行扩展，时间序列46～90 的数据与时间序列1～45 相同。

两种算法的融合效果随着样本数据的增加变化情况如图3 所示。

图3 不同算法融合效果对比2

从图3 可以明显看出：随着样本数据的增加，两种算法的融合效果越来越接近，即两种算法的权重分配趋于一致。主要原因是随着样本数据的增加，本文算法计算的各测量站测量精度越来越精确，且逐步逼近真实的精度值。

从以上分析可知，随着样本数据的增加，本文算法对权值的确定会越来越合理。

4.1.2 融合效果鲁棒性分析

为检验2 种算法融合效果的鲁棒性，假设第1部遥测设备受到环境的影响较大，其测量精度恶化为5 m。仍然进行100 次仿真，2 种算法的融合效果如图4 所示。

图4 不同算法融合效果对比3

从图4 中可以明显看出：算法1 的融合精度在3.5 m 左右，而本文算法的融合精度在1.5 m 左右；算法1 的融合效果远不如本文算法。主要原因是第1 部测量设备受到环境的影响，测量精度明显变差，而算法1 仍然以标称的测量精度赋予其最大的融合权重值，导致算法1 的融合效果明显较差；本文算法对测量设备实际的测量数据进行统计分析，比较准确地估算出各测量设备的测量精度，融合权重的确定更加符合实际情况，导致最终的融合效果仍然优于任何一部测量设备的测量精度。

从上述分析可知，本文算法的鲁棒性优于算法1。

4.1.3 结论

综上，考虑到测量设备的工作状态（正常或故障）以及测量精度（已知或未知）两方面的因素，本文算法的融合精度都能够确保优于任何一部测量设备的测量精度，算法1 并不能得到这样的融合效果。

4.2 与算法2 的对比分析

4.2.1 融合权值合理性分析

为检验两种算法权重确定的合理性，将表1 中样本数据进行扩展，时间序列46～90 的数据与时间序列1～45 相同。

两种算法的融合效果随着样本数据的增加变化情况如图5 所示。

图5 不同算法融合效果对比4

从图5 可以明显看出：本文算法的融合效果几乎始终优于算法2 的融合效果。主要原因是算法2通过分析不同雷达测量数据之间的相对关系，以修正证据距离确定不同设备之间数据融合的权值，该融合权值的确定不符合权值分配最优原则，导致最终的融合结果肯定劣于测量精度最高的遥测设备探测的实际数据。

从上述分析可知，算法2 中权值的计算并没有按照加权融合过程中最优权值的确定原则；本文权值的分配依据是加权融合过程中最优权值的确定原则。

4.2.2 融合效果鲁棒性分析

为检验2 种算法融合效果的鲁棒性，假设第1部遥测设备的测量精度为0.5 m。仍然进行100 次仿真，2 种算法的融合效果如图6 所示。

图6 不同算法融合效果对比5

从图6 中可以明显看出：算法2 的融合精度在1 m 左右，而本文算法的融合精度在0.5 m 左右；与第1 部测量设备的测量精度0.5 m 相比，算法2 的融合效果明显较差；由于本文算法依据对遥测设备实测数据的统计分析，进行不同测量设备测量精度的计算，因此，测量精度计算的精确性与遥测设备测量数据的数量直接有关。

从上述分析可知，本文算法的鲁棒性优于算法2。

4.2.3 结论

综上，本文算法的融合效果优于算法2。

5 结论

本文研究了靶场试验中遥测数据融合处理问题。通过研究得出如下结论：

1）在遥测设备测量精度已知，且所有遥测设备正常工作的情况下，基于遥测设备测量精度的最小二乘加权融合法融合效果最好。

2）在遥测设备测量精度未知，且所有遥测设备测量精度相差不大的情况下，利用多部遥测设备测量数据之间相互关系进行权重确定的加权融合方法，能够取得与最高测量精度相差不大的融合效果。

3）考虑到遥测设备实际工作状态、测量精度能否获取的情况，本文算法的融合效果优于最小二乘加权融合方法。

4）考虑到遥测设备技术参数差异情况，本文算法的融合效果，优于利用多部遥测设备测量数据之间相互关系进行权重确定的加权融合方法。

5）本文所提方法原理简单，易于编程实现，具有一定的理论参考和工程应用价值。