侵爆弹对框架类建筑物毁伤效果评估研究

张重阳，周 理，陈广阳，黄晓蔚，侯晓雯

（解放军66136 部队，北京 100042）

0 引言

爆炸冲击波是侵爆战斗部的主要毁伤元素，全面准确地认识并掌握爆炸的原理对评估建筑物的毁伤效果具有重要的作用。

空中爆炸作为一类典型的爆炸现象，对其规律研究的重点就是如何有效地分析爆炸效应对目标的毁伤机制。爆炸冲击波毁伤目标的研究方法可分为3 种：即试验研究、理论分析和数值模拟。由于爆炸及其作用过程的复杂性，理论分析和实验研究都有很大的困难。随着计算机技术的不断发展，目标毁伤数值模拟技术也愈加成熟。各种用于结构分析的数值模拟软件如雨后春笋般出现，比如ANSYS、AUTODYN、LS-DYNA、ABAQUS 等软件，经过近十几年的发展，已经逐渐成熟。

本文利用LS-DYNA 有限元软件，建立单枚侵爆弹在建筑物内爆炸的数值仿真模型，分析了建筑物的破坏情况及相应构件的毁伤情况，并对建筑物的毁伤效果进行了评估。在进行数值模拟时，由于壳体变形和破碎所消耗的能量约占炸药爆炸释放总能量的1%～3%［1］，对战斗部的威力不会有太大的影响，所以近似估算时可忽略不计。

1 毁伤判据与毁伤准则

1.1 建筑物毁伤判据

毁伤判据是目标在不同毁伤阶段的各类物理毁伤现象或功能系统失效情况的描述，是毁伤效果判别的主要依据。本文研究的目标为四层五跨框架结构类钢混建筑物，其主要的构件包括：梁、柱、楼板、剪力墙。在不同冲击波的作用下其毁伤程度可分为三级：轻微毁伤、中等毁伤以及严重毁伤。其具体的毁伤等级标准见参考文献［2］。

1.2 建筑物结构毁伤准则

在建筑物毁伤等级划分标准中，一般采用构件毁伤比率、目标修复时间等多类型定量判据综合评价建筑物的毁伤程度。根据以上原则可将框架结构类钢筋混凝土建筑物整体毁伤情况分为四级：轻微毁伤、中等毁伤、严重毁伤、摧毁。具体的毁伤等级划分标准见参考文献［2］。

2 数值模拟算法及有效性验证

2.1 数值模拟采用的算法

采用ALE 算法［3-5］模拟战斗部在建筑物内爆炸。经过阅读大量相关文献，发现现有结构分析程序中LS-DYNA 利用欧拉（Euler）和拉格朗日（Lagrange）耦合场分析计算得出的爆炸载荷最为合理。采用ALE 算法来描述炸药爆炸和建筑物破坏过程，对炸药和空气采用欧拉算法，对建筑物采用拉格朗日算法，然后通过流固耦合方式来处理相互作用（*CONSTRAINED_LANGRANGE_IN_SOLID）。这种方法的优势在于炸药和流体材料在Euler 单元中流动不存在单元的畸变问题，而且采用流固耦合方法来处理相互作用，能够方便地建立模型。ALE 算法能够解决因单元严重畸变所引起的数值计算困难，并且能够对流固耦合进行动态分析，兼具拉格朗日算法和欧拉算法的优点，是非线性连续介质力学中很有前景的分析方法。

2.2 模拟方法的有效性验证

所研究的目标为四层五跨框架类建筑物，侵爆弹爆炸的位置为楼道内。为了验证ALE 算法在这类场所的适用性，需要进行相应的试验研究。根据洛阳防护工程研究所进行的房屋内爆试验的数据，利用LS-DYNA 中的ALE 算法进行试验原型的数值模拟，通过对比试验值和计算值来验证模拟方法的有效性。

2.2.1 房屋内爆炸试验条件设置

用于内爆试验的房屋为框架结构。梁柱混凝土强度等级为C35；墙体采用实心粘土砖，厚度370 mm；结构底部、砖墙顶端各设一道240 mm×370 mm 圈梁。结构具体几何尺寸见图1。

图1 内爆试验房屋尺寸

试验时，在结构内部空间几何中心安放TNT 集团装药，分1 kg、2 kg 两种药量，电雷管起爆。主要测量参数包括：房屋后墙中轴线距地面39.5 cm、181.3 cm、321.5 cm 处空气冲击波超压；侧墙中轴线距地面45.1 cm、186 cm、326.2 cm 处空气冲击波超压；屋顶梁L2 几何中心及距几何中心50 cm 处垂直方向加速度。试验测点的布置示意如图2 所示。

图2 试验测点布置示意图

2.2.2 房屋内爆炸数值模拟

首先建立房屋内爆炸的有限元模型，如图3 所示。其中TNT 炸药与空气采用共结点建模，并采用Euler 单元描述，建筑物则采用Lagrange 单元描述，两者之间通过流固耦合进行相互作用。

图3 房屋计算实体模型

利用LS-Prepost 后处理软件提取模型中与测点对应位置的超压、加速度结果进行比对。W=1 kg时各测点超压数值模拟结果如图4 所示，W=2 kg 时各测点加速度数值模拟结果如图5 所示。

图4 空气冲击波超压计算值（W=1 kg）

图5 加速度计算波形（W=2 kg）

2.2.3 数值模拟结果与实测结果对比

读取数值模拟结果和实测结果超压值的波形峰值进行比对，如表1 所示。读取数值模拟结果和实测结果加速度值的波形峰值进行比对，如下页表2 所示。

表1 超压试验值与计算值比较

比较表1 和表2 中数值模拟结果与试验结果可知，计算与试验之间的误差均不大于20 %，这对爆炸这类强动载问题的试验与计算来说是可以接受的，其中冲击波的实测值与计算值之间的误差最小。换言之，通过流固耦合方法来计算炸药与结构的相互作用是可行的。

表2 超压试验值与计算值比较

3 单枚侵爆弹在典型建筑物内爆炸数值模拟

3.1 计算模型的建立

进行炸药对建筑物的爆炸冲击数值模拟时，由于实际建筑物较大，为了节约计算成本，减少计算量，鉴于建筑物的对称性，取其1/4 建立有限元模型。计算模型的建立涉及到两方面的尺寸：炸药尺寸和建筑物尺寸。

3.1.1 炸药

战斗部装药按等效TNT 当量来计算，其等效TNT 当量为177.1 kg，假设其形状为长方体，边长分别为60 cm、60 cm 和30 cm。

3.1.2 建筑物

根据本文所要研究的内容，建筑物选取为四层五跨框架结构建筑。每间房子长和宽为600 cm，层高360 cm，柱为80 cm×80 cm，梁为60 cm×40 cm，楼板第1 层厚30 cm，其余厚25 cm，轻质隔墙厚20 cm。

3.2 材料本构模型与状态方程

材料模型主要是表达材料在各种作用力下的应力应变关系，用正确的数学模型来反映这种关系是进行有效数值模拟的重要前提。

3.2.1 炸药的本构模型和状态方程

炸药采用MAT_HIGH_EXPLOSIVE_ BURN 材料模型和JWL 状态方程共同描述［6-7］，用燃烧反应率与高能炸药状态方程的乘积来控制爆炸过程化学能的释放。表达式如下：

其中，F 为炸药燃烧反应率，PEOS为来自于状态方程炸药的爆轰产物压力，P 为任意时刻炸药单元所释放的压力，V 为当前相对体积，E 为炸药的初始比内能，A、B、R1、R2和ω 为材料常数。装药采用TNT 炸药进行计算，其JWL 状态方程参数参考文献［8-9］。

3.2.2 空气的材料模型和状态方程

欧拉网格中的空气采用MAT_NULL 材料模型［10］。欧拉网格具有空间坐标属性，网格节点固定在空间中，物质在网格间运动、变形。这种材料模型可以通过调用线性多项式状态方程EOS_LINEAR_POLYNOMIAL 描述空气压力和密度的关系：

表3 多项式状态方程参数

3.2.3 混凝土的材料模型

混凝土的材料模型采用H-J-C 模型，主要的性质及参数参考文献［11］。

3.3 有限元模型

对于爆炸而言，具有破坏作用的因素有：爆轰物的直接作用、爆轰物向四周的抛掷作用、地震波及空气冲击波的作用。根据以往大量的实验及仿真结果，爆轰物的直接及抛掷作用范围较小，而且地震波对目标的破坏作用相对远空气冲击波来说非常小，因此，在进行数值模拟时，着重考虑空气冲击波对建筑物的破坏效应。建筑物目标可简化为一幢四层五跨的框架结构，在2 层走廊中心点爆炸时，为了减少计算量建立1/4 模型，整体有限元模型如图6 所示，图中PART1 为梁、板和柱，采用共结点建模，PART2 为轻质隔墙，PART3 炸药，PART4 为空气，炸药与空气采用共结点建模。其中TNT 装药与空气采用Euler 单元描述，建筑物采用Lagrange 单元描述，炸药与建筑物之间通过流固耦合进行相互作用。

图6 整体有限元模型图

3.4 建筑物整体及框架的破坏情况

图7 和图8 分别是2 层走廊中心点时建筑物整体的破坏情况及框架的破坏情况。在这种情况下，相当于在整个走廊通道内爆炸。由于是在密闭空间中爆炸，所以对构件的毁伤程度较大，导致中间房间对应的上下层走廊楼板被完全摧毁，其他房间对应的走廊楼板出现剪切破坏。冲击波传播到走廊两端时，导致走廊前后墙被完全摧毁，且对两端的柱子造成中等毁伤，其他柱子属于轻微毁伤或未毁伤。对于轻质隔墙，由于其抗压能力较小，所以2、3 层的轻质隔墙破坏比较严重。

图7 建筑物整体破坏情况

图8 建筑物框架破坏情况

3.5 构件毁伤等级与毁伤数量情况统计

利用LS-Prepost 后处理软件观察建筑物构建的毁伤状态，可以得到各构建的毁伤数量和毁伤等级，如表4 所示。

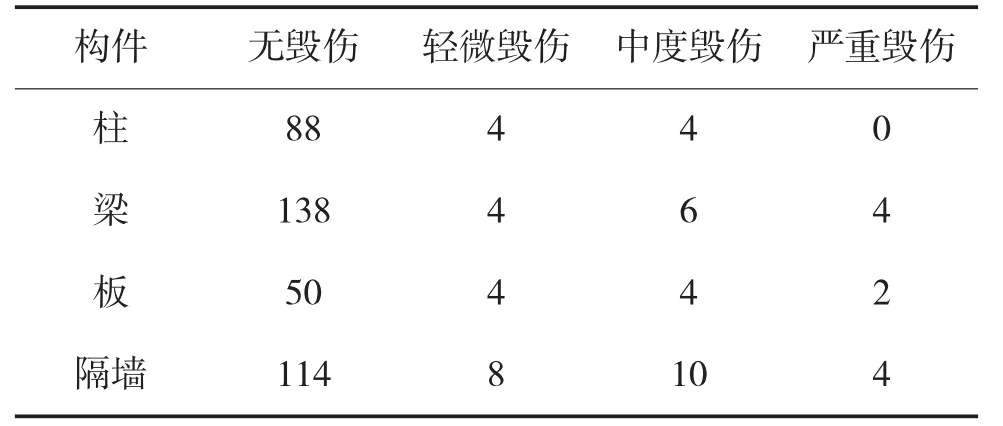
表4 单枚弹在2 层走廊中心爆炸构建毁伤情况

4 毁伤效果评估模型

4.1 物理毁伤等级划分及大楼层次结构

建筑物为四层五跨框架类钢筋混凝土建筑物，其主要的承力结构为柱、梁、板。根据不同结构形式的钢混结构建筑物其结构构件类型不尽相同的实际情况，参考冲击波作用下的评判指标，建立框架结构的层次结构图，通过分析，建立了如图9 所示的层次结构图。

4.2 建筑物毁伤等级的模糊综合评判模型

4.2.1 因素集的确定和划分评语集

4.2.2 隶属函数的确定

图9 框架结构整体毁伤的层次结构图

隶属度选取原则：确定区间中点隶属于该毁伤等级的隶属度为1。将严重毁伤等级的下界稍做外延，隶属函数仍然选F 分布中的三角分布。

1）构件受到毁伤比例P 的隶属函数

2）不同构件受到毁伤比例的隶属度函数如图10 所示。

图10 构件受毁伤比例P 的隶属函数图

4.2.3 指标权重的确定

指标权重的确定采用AHP 法［12-14］，对于定性和定量地解决问题具有较好的实用性，对于本问题具体的计算模型如下：

1）确定影响建筑物毁伤情况的因素，根据对框架结构的分析可知影响建筑物毁伤情况的因素主要有四类：柱、梁、板及轻质隔墙；

2）利用1～9 标度法对这4 种因素进行两两比较并经过量化，可以得到量化的判断矩阵

4.2.4 合成算子的选择

4.2.5 模糊综合评价向量的处理

4.3 单枚弹打击典型建筑物毁伤效果评估算例

单枚弹打击典型建筑物时，选择战斗部在2 层走廊中心点爆炸的情况进行计算。战斗部在2 层走廊中心点爆炸时，由爆炸数值模拟，可以得到建筑物各构件的毁伤数量与毁伤等级，如表4 所示。

2）根据建筑物构件各毁伤等级的比例P 和毁伤等级的隶属度函数ui（P），可以得到柱、梁、板和轻质隔墙的隶属向量r1、r2、r3、r4，由此可以得到隶属度矩阵R，其中

5 结论

本文采用LS-DYNA 程序中的流固耦合算法来模拟侵爆弹对典型建筑物的毁伤效果，通过房屋内爆炸试验和等效原型的数值模拟验证了该方法的有效性，而后建立了四层五跨框架类钢混建筑的有限元模型，并对单枚侵爆弹在2 层走廊中心点爆炸进行了数值模拟，得到了建筑物构建的毁伤数量和毁伤等级，然后建立建筑物毁伤等级的模糊综合评判模型，对炸点在2 层走廊中心时的毁伤效果进行了计算，其结果为中度毁伤。采用的方法为建筑类目标的毁伤效果评估工作提供了一定的借鉴。