让概念的核心内涵在层层对比中自然呈现

张缅 高丛林

【课前慎思】

“认识一个整体的几分之一”是苏教版数学三年级下册第七单元起始课。在此之前，学生已经学过把一个物体或图形平均分成若干份，用分数表示这样的一份或几份，在生活中也积累了很多平均分一个物体，用分数表示分的结果的经验。本节课的学习内容既丰富了学生对分数的理解，也是今后进一步抽象分数的意义、理解分数的性质的重要支撑。

“认识一个整体的几分之一”对于三年级学生来说非常抽象。首先，就分数外形来说，本节课学习的分数和以前的分数没有差别。把一个桃子平均分成两份，每份用表示，把一盘桃子平均分成两份，每份也用表示。可是它们对应的数量却不同，前者是半个，后者可以是1个，可以是2个、3个，甚至100个……这一改变在学生认识数方面将带来思维上的飞跃。以前数表示的大小是固定的，数与量的关系一一对应，而现在同一个分数可以对应不同的数量，不同的分数对应的数量也可能是相同的。这对学生认知造成很大的冲突。其次，就分数的意义来说，把几个物体组成的整体平均分成若干份，用分数表示这样的一份，仅仅是部分和整体间的关系，其结果与一份的实际数量在形式上完全不同。比如，把6个桃子平均分成3份，每份是这盘桃的，这里表示一份和这盘桃子的关系，这与原有经验“每份有2个桃子”存在很大的认知差异。

“难道同一个分数却有两种甚至更多种意义？”“究竟什么是分数？”学生认知上产生很大困惑。面对这些既有联系又有区别的新旧概念，“比较”是有效的教学方法。顺应学生思维，一次次引导学生通过操作、观察、思考，从不同角度、不同层面开展对比和辨析，对比中，学生层层突破对分数原有的单一认识，去伪存真，渐渐逼近分数的本质;对比中，学生悟到分数与具体个数无关，只和平均分的份数有关。不管是一个物体还是多个物体，只要把它或它们看作一个整体，平均分成几份，每份就是这个整体的几分之一。分数的本质在层层对比中自然地浮出水面，学生的思维在层层对比中不断进阶。

【教学目标】

1. 在具体情境中进一步认识分数，知道把一些物体看成一个整体平均分成若干份，每份可以用几分之一来表示。

2. 通过动手操作、合作交流、提问释疑、自主探索等学习活动，经历探索、发现“用分数表示一些物体的几分之一”的知识获取过程，能用自己的语言来描述分数的含义。

3. 在有趣的情境中参与对分数的新探索、新发现、新认识活动，感受学习数学的快乐，体会分数与现实生活的联系。

【教学过程】

对比一：沟通新旧知识，初步感受一个整体的几分之一

师：（播放视频）夏天到了，尼克又做了许多爪爪冰分给小仓鼠们。只剩一个爪爪冰了，却有两只小仓鼠等着要。想想怎样分公平？

生：平均分。

师：你能用一个分数表示分的结果吗？为什么？

生：把一个爪爪冰平均分成2份，每份是半个，每份是这个爪爪冰的。

师：两只小仓鼠各吃了半个很不过瘾，第二天尼克又准备了一些爪爪冰，他想平均分给这两只仓鼠。每只小仓鼠能分得这盘爪爪冰的几分之几呢？

教师课前给学生每人准备一个装有爪爪冰图的信封，爪爪冰数不同。请学生“分一分”“涂一涂”，表示出每只小仓鼠分得这盘爪爪冰的几分之几。

展示，请几个同学把作品贴在黑板上。

生1：我的这盘爪爪冰一共有6个，把它平均分成2份，每份是3个，这3个就是这盘爪爪冰的。

师：这3个爪爪冰（指涂色部分）就是这盘的，这3个爪爪冰呢（指没涂色部分）？是这盘的几分之几？

师：咦，奇怪了，分的是6个爪爪冰，涂了色的有3个，怎么会用表示？

生：我们是把这6个爪爪冰看作一个整体（师相机用红笔在图中画集合圈）平均分成2份，所以每份就是这盘爪爪冰的。

师：回顾一下，刚刚平均分一个爪爪冰和现在平均分一盘爪爪冰，两次分有什么相同和不同？

生：都是平均分成2份，取其中一份。

生：一个是把一个爪爪冰平均分2份，一個是把6个爪爪冰当作一个整体平均分成2份。

【点评：从一个物体的几分之一到一个整体的几分之一，这是分数含义的一次主要拓展。将新旧知识融合在同一个有趣的情境中，充分利用“都平均分成两份”这个连接点，突出重点，化难为易。把一个爪爪冰平均分成两份，每份是个，是一个爪爪冰的，这里前一个是量，后一个才是一份和整体的关系，具有分数最本质的含义。把6个爪爪冰平均分成两份，每份不可能再是个了，每份的个数变了，但每份仍然是一个整体的，平均分的份数一样，分数的本质没变。由分一个爪爪冰到分一盘爪爪冰，抓住了新旧知识的同化和顺应，启发学生用原有的经验探索新知，实现知识的迁移。】

对比二：变化中的不变，再次体验一个整体的几分之一

师：再看看其他同学分的情况。

生1：我的这盘爪爪冰一共有4个，把它们看作一个整体，平均分成2份，每份是2个，这2个爪爪冰就是这盘爪爪冰的。

师：为什么这两个爪爪冰就是这盘的？

生1：因为我把4个爪爪冰看作一个整体。

生2：我的这盘爪爪冰一共有8个，我把它们看作一个整体，平均分成2份，每份是4个，每份就是这盘爪爪冰的。

生3：我的这盘爪爪冰一共有10个，我把它们看作一个整体，平均分成2份，每份是5个，每份就是这盘爪爪冰的。

生4：我的这盘爪爪冰一共有5个，我把它们看作一个整体，平均分成2份，每份是两个半，每份也是这盘爪爪冰的。

师：这位同学分的结果很特别，每份出现了半个的情况，为什么？每份也能用表示吗？

师：观察这些分的情况，有什么相同和不同的地方？

生：相同点是都把盘子里所有爪爪冰看成一个整体;都是平均分成2份;每份都用表示。

生：不同点是总个数不同;每份的个数也不同。

【点评：在探索新知的过程中，教师为学生提供了多样的学材，组织了丰富的活动。每个学生都经历了从图到分数，再到根据分数画图的过程，从正反两个方面理解将一个整数平均分成2份都用来表示。当不同的作品展示出来，学生通过观察比较，发现尽管每份的爪爪冰数各不相同，但都是两份中的一份，都可以用表示。这样在变化中发现不变，有利于学生洞悉数学本质。】

对比三：不变中的变化，归纳概括一个整体的几分之一

师：这时，又来了一只小仓鼠。尼克要想把这6个爪爪冰平均分给3只小仓鼠，每只小仓鼠分得这盘爪爪冰的几分之几？

（学生再次“分一分”“涂一涂”，表示出每只小仓鼠分得这盘爪爪冰的几分之几）

生：我是把这6个爪爪冰看作一个整体，平均分成3份，所以每份就是这盘爪爪冰的。

师：我们之前也分了6个爪爪冰，都是6个爪爪冰，为什么却用了不同分数表示？

生：因为平均分的份数不同，之前是平均分成2份，每份是这盘爪爪冰的，现在平均分成3份，每份是这盘爪爪冰的。

师：尼克还有一盘爪爪冰，他想再邀请几个小仓鼠来品尝，你要是尼克会邀请几只小仓鼠呢？看，这盘里有12只爪爪冰，请你帮忙把这些爪爪冰平均分给邀请来的小仓鼠吧。

生：把12个爪爪冰看作一个整体，平均分成3份，每份4个，是这盘爪爪冰的。

生：把12个爪爪冰看作一个整体，平均分成4份，每份3个，是这盘爪爪冰的。

……

师：平均分的都是12个爪爪冰，为什么表示每份的分数却不一样呢？

生：平均分的份数不同。平均分成几份，每份就是这个整体的几分之一。

师：对了，刚刚有同学想要邀请5只、10只仓鼠的，你们怎么改主意了？

生：分得不方便。

师：能分吗？分的结果怎么表示？

师：是的，平均分成几份，每份就是几分之一。只是在实际分的时候我们还要考虑数据特点，不然尼克分得不方便，仓鼠吃得也不过瘾。

师：今天我们又认识了分数，（板书课题：分数的初步认识2）这些分数有什么共同之处？

生：都是把一个整体平均分成几份，每份是这个整体的几分之一。

师：今天学的分数和之前有什么不同？

【点评：经过之前的比较和概括，学生已经将关注点放在了研究部分和整体之间的关系上，不再受具体个数的干扰。先思考同样6个爪爪冰，平均分成3份，每份怎么用表示，让学生初步感受分数和爪爪冰总数无关，只和平均分的份数相关。再出示12个爪爪冰图，让学生自主操作，变换平均分的份数，进而发现整体不变，但平均分的份数变了，那么表示每份的分数也变了。通过对分子分母意义的思考，逐步完善分数意义的建构。这个环节的教学共融合了四次小对比，都是分6个爪爪冰和分12个爪爪冰所得到不同分数的对比、今天学习的分数之间对比以及今天学习的分数和之前学习的分数之间的对比。在一系列对比下， “把一些物体看作一个整体，平均分成几份，每份就是它的几分之一”自然地浮出水面。】

对比四：变式练习，深度理解一个整体的几分之一 。

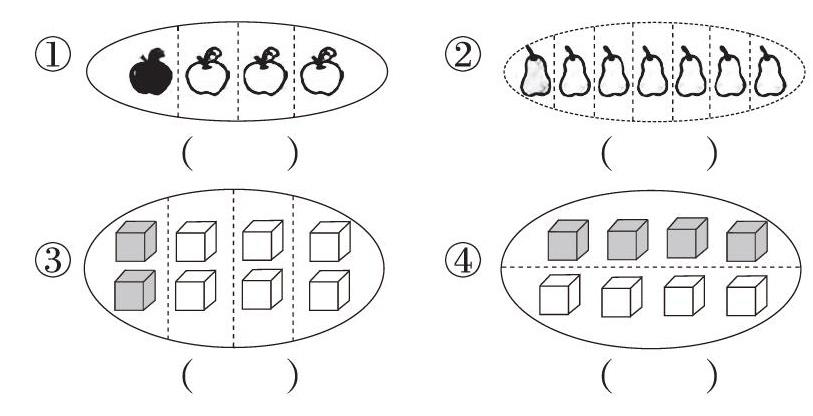
1.分完爪爪冰，尼克又给仓鼠们分了水果和积木。你能用分数表示涂色部分吗？

追问：①和②对比，你有什么发现？

生：每一份都是1个，但是表示每份的分数却不一样。

师：看来不同分数表示的数量可以相同。

师：再看①和③，他们都是用表示，为什么一个涂了1个，另一个涂了2个？

生：因为总数不同。

师：看来相同分数表示的数量可以不同。

师：再比较③和④，你有什么发现？

生：都是8个小正方体看成一个整体，平均分的份数不同，每份不同，表示每份的分数也不同。

【点评：一道习题组织了三个层次的对比：（1）通过①和②對比，学生发现每份虽然都是一个物体但却用不同分数表示，突出了“不同分数相对应的物体数量可能是相同的”。（2）通过①和③对比，学生发现都是，有的是1个物体，有的是2个物体，突出“同一个分数相对应的物体数量也可以是不一样的”。 （3）再通过③和④的对比，同样是8个小正方体，每份可以是，也可以是，突出了“平均分成几份每份就是几分之一”。三个角度的对比，倒逼学生深度理解几分之一的本质，促使学生知识的内化，引领学生思维不断进阶。】

2.分爪爪冰游戏

师：尼克给我们带来9个爪爪冰，我们一起玩个小游戏。谁能取走这些爪爪冰的？（拿走3个）

师：谁还能取出剩下爪爪冰的？（拿走2个）

师：都是，为什么有人取了3个，有人却取了2个呢？

师（指出）：尽管都是，但因为整体变了，所以整体的所表示的数量也就跟着变了。

师：谁再来取走剩下的？（拿走2个）

师（追问）：为什么又拿走了2个？

师：再取走剩下的？（拿走1个）再取走呢？（拿走）……

师：像这样，不停取下去，能取得完吗？

【点评：结尾部分的游戏设计是全课的点睛之笔。首先，它依然统一在分爪爪冰的情境中，保持着全课故事的连贯性。其次，它具有很强的操作性，学生兴趣盎然。最重要的是，它是一组综合性练习，也体现了3次对比。取和再取剩下的对比，突出整体变了，同一个分数表示的数量也变了;取和取对比，突出整体变了，同样数量可以用不同分数表示;再取剩下、再取剩下……引发学生思考整体可以是多个物体，也可以是1个物体，甚至可以不足1个物体，整体的数量不重要，只要看成一个整体，平均分成几份，每份都是这个整体的几分之一。不仅直击分数本质，还渗透无限思想，意蕴深长。】