加筋板破坏载荷计算中的蒙皮有效宽度计算方法适应性验证

吴存利，聂小华

(中国飞机强度研究所 计算结构技术与仿真中心， 西安 710065)

0 引 言

结构稳定性是飞机结构设计中最为关心的问题之一，飞机薄壁静强度失效中很大一部分是因为丧失稳定性引起的，由于结构稳定性约束的限制，飞机结构设计应力远远小于结构材料的许用应力。因此，保持稳定性是不同薄壁结构形式的选择和设计的主要依据。

对于金属结构的稳定性分析，已经形成了一系列分析方法，并形成了各种手册。如美国最早的Handbook of Structural Stability，Part I-VI[1-5]，该手册全面讨论了平板的屈曲，组合元件的屈曲，曲板和壳体的屈曲，板和组合元件的破坏，加筋平板的破坏。该手册是结构稳定性分析的鼻祖，后来国内外出版的书、手册和指南提供的关于稳定性分析方法都来自于该手册。

我国1965年8月出版的《飞机设计员手册(第四册)》和1983年4月出版的《飞机设计手册(下册)》中均介绍了金属飞机结构的稳定性计算方法。在1996年6月出版的《结构稳定性设计手册》中，较全面地总结了我国飞机设计部门多年的设计经验和大量试验研究数据，给出了金属飞机结构稳定性分析的较完整的计算公式、设计曲线和实用分析软件[6]。

金属加筋板的受压破坏形式，根据有效长度大小可分为三种。在长柱范围内，即长加筋板，其破坏形式呈弹性弯曲失稳破坏(又称柱失稳)，在这一区间,采用欧拉公式计算。在短柱范围内，属于塑性压缩破坏，即压损破坏。在中长柱范围，属于塑性失稳破坏，工程中一般采用两种方法,第一种方法为抛物线近似法；第二种为Johnson-Euler方程。目前国内外飞机设计公司如空客、庞巴迪、中国商飞多采用第二种方法[7-9]。

采用Johnson-Euler方程，必须计算蒙皮的有效宽度。目前关于有效宽度的计算存在着多种方法，但未见有公开的文献对计算方法的来源和适应性进行说明。鉴于此，本文针对国内外飞机设计人员常用的有效宽度计算方法进行讨论研究，探讨其来源，并针对Z型加筋板，说明其适应性。

1 Johnson-Euler方程

Johnson-Euler方程在抛物线近似法[10-13]基础上简化而来，抛物线近似法为

(1)

(2)

采用Johnson-Euler方程计算加筋与蒙皮有效宽度组成柱的破坏应力，涉及柱的面积和惯性矩的计算，而其中的关键就是确定蒙皮的有效宽度，一旦蒙皮的有效宽度已知，则采用式(2)能较为容易的得到加筋板的许用应力。

2 有效宽度概念和计算方法

有效宽度示意图如图1所示。假设加筋板受到如图1(a)所示的轴压载荷，随着加载的继续，加筋板截面上载荷分布变化情况如图1(b)所示。

在达到板的初始失稳应力之前，整个截面应力分布比较一致。当应力超过板的初始失稳应力后，加筋之间的薄板发生屈曲，不再承受大于临界屈曲载荷的载荷，但是与加筋连接的这部分薄板，由于与加筋相连仍有继续承载的能力，工程中把与加筋相连的薄板的宽度称作有效宽度，如图1(c)所示。在加筋之间的薄板屈曲后，加筋板截面应力分布变得不再均匀，筋条根部应力较大，离筋条越远应力基本保持为常值(如图1(b)所示)。工程上为了计算方便，用一致的应力分布来代替不一致的应力分布，取中间板的初始失稳应力和板边最大应力代替不一致应力分布，如图1(d)所示。由以上分析可知，当载荷继续增加，有效宽度会越来越窄，如图1(b)所示。因此确定加筋薄板的有效宽度成为计算加筋板破坏载荷的关键因素。

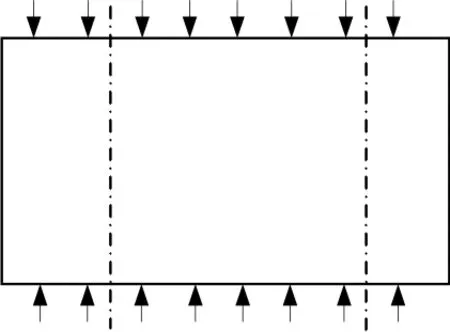
(a) 结构示意图

(b) 有效宽度的取法

(c) 理论有效宽度

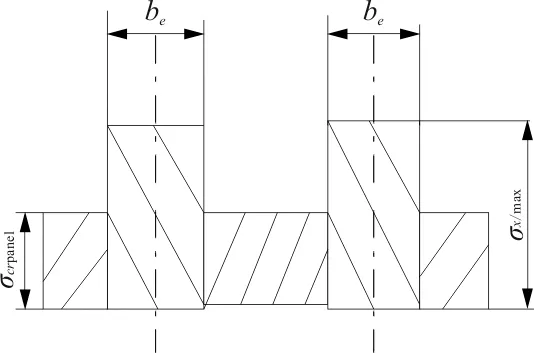
(d) 应力的近似处理

目前国内外对有效宽度计算有下列8方法。

2.1 Von Karman有效宽度

在刚开始加载到筋条间板发生局部屈曲之前，应力分布是均匀的，当筋条间板失稳后，应力开始变得不再均匀，随着压缩载荷的增加，失稳的区域越来越多，内力越来越向筋条附近转移，使其有效宽度变窄(如图1(b)所示)。由板局部屈曲理论分析可知，加筋板的初始屈曲应力即为两筋间板的局部失稳应力，即

(3)

式中：b为两筋条之间蒙皮宽度；t为蒙皮厚度；E为蒙皮弹性模量；ν为材料泊松比；kc为压缩临界应力系数，与板的边界支持条件及长宽比(a/b)有关。

Von Karman认为，加筋板结构的最终失稳应力可用筋条附近的一块有效宽板的临界失稳应力来表征[14]，于是，当b为有效宽度be时，σcr应为筋条的最终失稳应力σst即，如式(4)所示。

(4)

由式(3)和式(4)得出：

(5)

2.2 Winter有效宽度

Winter对式(5)作了修正，给出的有效宽度表达式[15]：

(6)

式中：ξ为修正项，其表达式为

(7)

2.3 牛春匀书中的有效宽度

牛春匀在《实用飞机结构应力分析及尺寸设计》中推荐采用如下的有效宽度计算公式[16]：

(8)

式中：Kceff为蒙皮屈曲系数，与边界条件和蒙皮几何尺寸相关，其表达式为

(9)

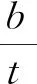
2.4 Bruhn书中的有效宽度

针对不同类型的加筋板，Bruhn在《Analysis and Design of Flight Vehicle Structures》中采用如下有效宽度计算方法[11]。

(a) Z和J形剖面铆接加筋板

有效宽度计算方法为

(10)

式中：t为蒙皮厚度；E为弹性模量；σst为筋条应力(对于短板，σst=σcc)。

(b) L、Ⅰ形剖面铆接连接

对每个凸缘用双排铆接线与蒙皮连接在一起的L、Ⅰ形剖面铆接加筋板如图2所示。在工程计算中，一般仍按一排铆接线计算，即be仍用式(10)计算，如图3(a)所示。但在计算筋条压损应力时，与蒙皮相连的缘条厚度取缘条厚度与蒙皮板厚度之和的3/4，如图3(b)所示。

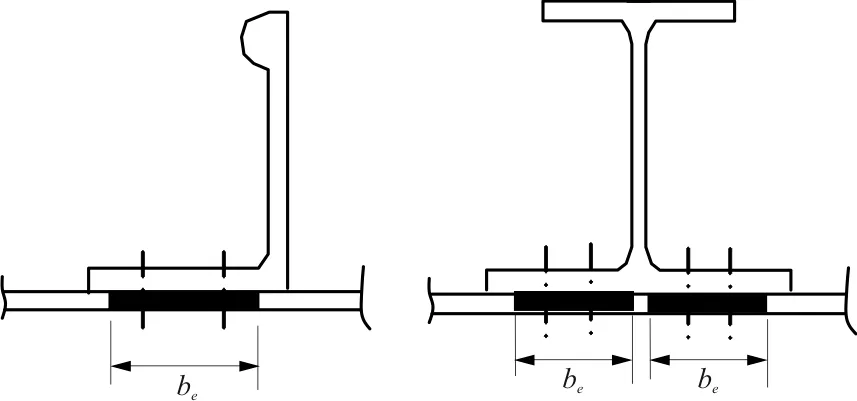
(a) L形剖面 (b) Ⅰ形剖面

图2 L和Ⅰ形剖面

Fig.2 Sections of L and Ⅰ

(a) 情况1

(b) 情况2

对于情况1，筋条的压损应力按T形截面计算，T形截面的垂直部分视为两头简支，即be仍用式(10)计算，但蒙皮厚度取为t=(ts+tf)/2。

对于情况2，筋条压损应力按Ⅰ形来计算，有效宽度be仍用式(10)计算。

(c) 蒙皮一端自由

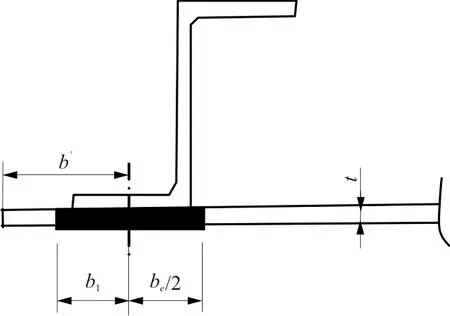
图4 蒙皮一端自由

如果蒙皮与筋条的材料不同，be可用式(11)计算。

(11)

式中：σst为筋条应力；σsh与筋条有同样应变时蒙皮的应力；Est筋条的弹性模量。

2.5 “民机指南”中有效宽度

由航空工业出版社出版，孙侠生主编的《民用飞机结构强度刚度设计与验证指南》，有效宽度计算方法[12]为

(12)

式中:ts为蒙皮的宽度；br为铆钉间距，单位：mm。

2.6 工程有效宽度简便计算方法

工程中采用如下简便的计算方法(简称30t)[12]，对于2024系列材料，蒙皮有效宽度为

be=br+30ts

(13)

对于7075系列材料，蒙皮有效宽度为

be=br+25ts

(14)

式中:ts为蒙皮的厚度；br为铆钉间距。

2.7 《飞机设计手册》中有效宽度

航空工业在1998年组织相关专业技术专家编写了《飞机设计手册》。在手册中蒙皮有效宽度选取方法[10]如下。

对于长桁和蒙皮材料相同的情况下，相邻蒙皮的有效宽度为

(15)

如果蒙皮和筋条材料不同，则有

(16)

式中：σs为筋条有同样应变时蒙皮的应力；Est为筋条的弹性模量。

2.8 国外民机设计公司蒙皮有效宽度

空客公司在对中长加筋板强度设计时，也采用Johnson-Euler方程计算。需要值得注意的是，空客手册中有效宽度计算方法，是建立在对Johnson-Euler方程修正的基础上，因此不具有通用性。

加拿大庞巴迪公司在中长加筋板极限强度计算中，蒙皮的有效宽度计算方法与牛春匀介绍的一致，因此这里不再介绍。

3 有效宽度计算方法评述

上面介绍了蒙皮有效宽度各种计算方法。下面将对这些计算方法进行简述。

Von Karman的有效宽度计算方法是从板的临界屈曲应力公式推导而来的，是最基础的，后面其他计算方法都是从该方法演变而来的。

Winter在Von Karman有效宽度计算方法的基础上增加修正项，由于修正系数小于1，用Winter方法计算得到有效宽度小于Von Karman的。

牛春匀采用的有效宽度计算方法与Von Karman的一致。如果将平板临界屈曲应力计算公式σcr=KceffE(t/b)2代入Von Karman计算公式，即得到牛春匀的计算方法。

Bruhn介绍的有效宽度计算方法，是牛春匀方法Kceff=3.62一种特殊情况，即认为筋条对蒙皮的支持为简支，是牛春匀方法一种特例。

“民机指南”中有效宽度在Von Karman公式的基础上按蒙皮的厚度进行了分类：当蒙皮厚大于3.15 mm，屈曲系数取简支；当蒙皮厚小于2.54 mm，屈曲系数取固支；当蒙皮厚在2.54 mm到3.15 mm，取简支和固支的平均值。

《飞机设计手册》第9分册给出的有效宽度计算方法与Bruhn给出的公式一致。

庞巴迪公司在《应力和疲劳手册》中的蒙皮有效宽度计算方法与牛春匀介绍的一致。

从上述分析可知，无论是国外民机设计手册，还是教材或科技书籍，所采用的有效宽度根源都来自Von Karman，不同之处是他们在Von Karman有效宽度的基础上增加了修正项，或是Von Karman的方法一种特例。

4 有效宽度计算方法适应性验证

鉴于上述的分析结果，本文利用机身加筋板试验数据，对有效宽度的Von Karman、Winter、Bruhn、“民机指南”、工程简便计算方法适应性进行验证，说明其计算效果。

4.1 试验件

机身壁板的轴压试验件共有12种构型，蒙皮曲率半径为1 560.9 mm。采用的材料为2524-T3和2524-T4，框和筋条所用的材料为7075-T62和7075-T6。

轴压壁板结构总长有542 mm和610 mm两种，总宽有580 mm和540 mm两种，试验段分别为492 mm和560 mm，夹持高度均取25 mm，长桁间距为190 mm和180 mm，蒙皮壁板为整体化洗，最厚处为1.6 mm，最薄处为1.0 mm。筋条为Z型剖面，按厚度以及形状分为5种类型。试验件详细构型和边界条件详见参考文献[17]。轴压试验件示意图如图5所示。

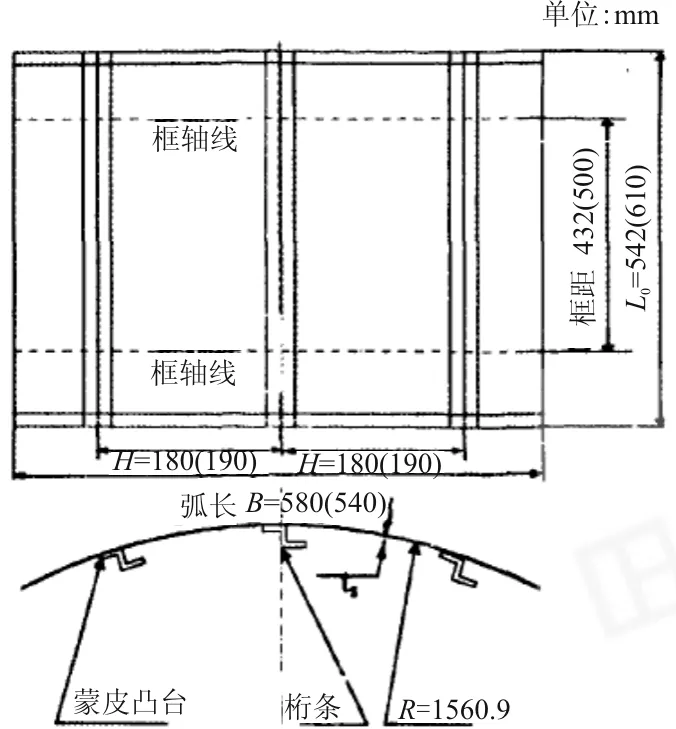
图5 机身壁板轴压试验件尺寸

4.2 加筋板破坏载荷分析

采用Johnson-Euler方程计算加筋板破坏载荷，需要先计算加筋条的压损应力，然后通过迭代获得加筋板的有效宽度，最后计算加筋板破坏载荷。

4.2.1 筋条压损应力

筋条的压损应力计算采用板元法[10-13]，依次计算各个板元的压损应力，然后计算筋条的压损应力。试验件5类筋条的压损应力计算值如表1所示。

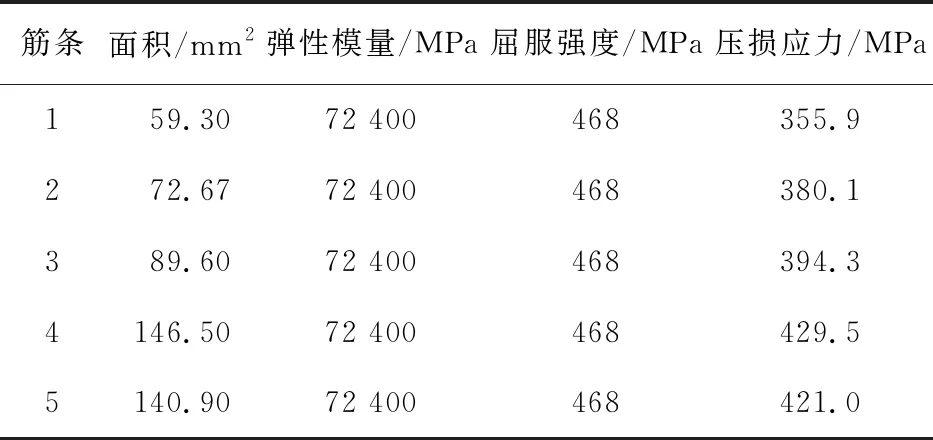
表1 筋条的压损应力

4.2.2 蒙皮有效宽度

对12种试验件构型，采用5种方法(Von Karman，Winter，Bruhn，“民机指南”，工程30t蒙皮厚度)计算了蒙皮的有效宽度，计算结果如图6所示。

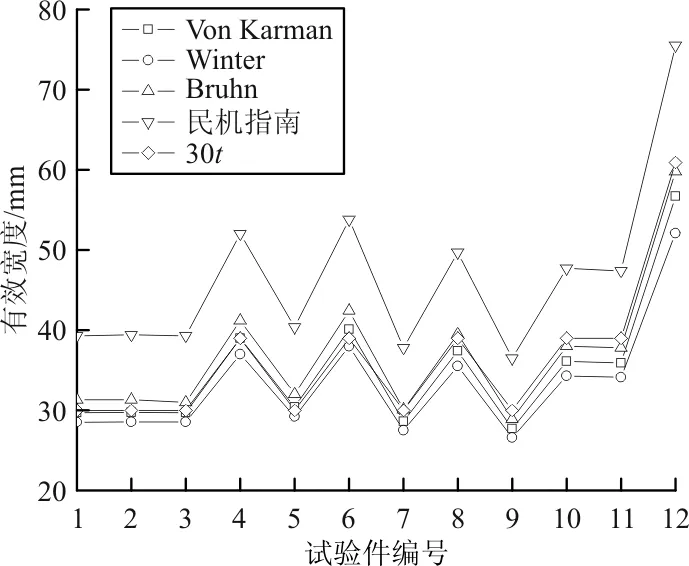
图6 蒙皮有效宽度

从图6可以看出：采用Winter方法得到的有效宽度值最小，其次是Von Karman方法，而采用民机指南得到的有效宽度最大；除了民机指南方法外，无论是Von Karman还是Winter或Bruhn方法，计算得到的有效宽度差异性不大，其值大小基本等同于30t的蒙皮厚度。

4.2.3 壁板破坏载荷

在得到蒙皮的有效宽度后，利用Johnson-Euler方程计算加筋板的破坏载荷。在计算中，端部支持系数取1.6(由试验确定)。

加筋壁板的破坏载荷如图7所示。

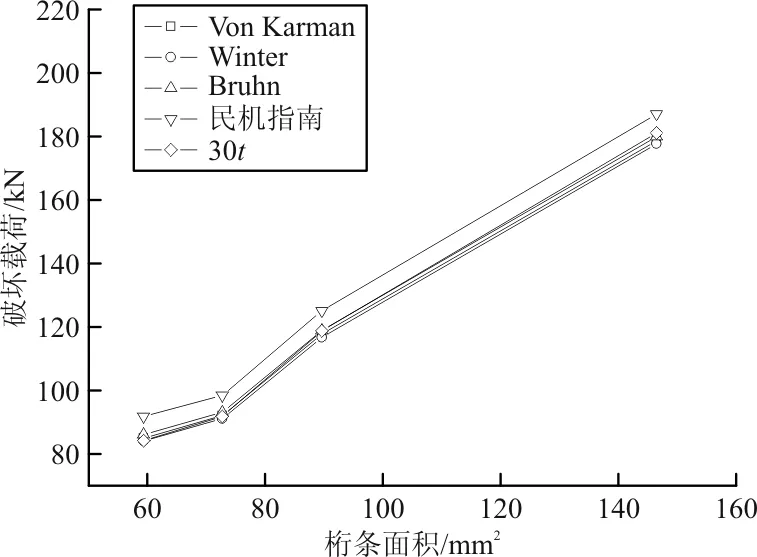
(a) 蒙皮厚度t=1.0 mm

(b) 蒙皮厚度t=1.3 mm

从图7可以看出：除了民机指南外，采用其他方法计算蒙皮有效宽度，然后利用Johnson-Euler方程得到的破坏载荷基本相同。如果采用民机指南，计算得到破坏载荷比其他方法大约大10%。也可以看出，在蒙皮厚度一定的情况下，加筋板的破坏载荷随筋条面积的增加而增大。

计算值相对于试验值的误差曲线如图8所示，试验值取自文献[17]。

(a) 蒙皮厚度t=1.0 mm

(a) 蒙皮厚度t=1.3 mm

从图8可以看出：无论采用何种有效宽度计算方法，除了少数几个值外，其他值都在±10%之内，这说明采用Johnson-Euler方程计算得到的破坏载荷误差大约在10%之间；对于Z字型加筋板，在蒙皮厚度一定的情况下，计算误差随筋条的面积增大由正变为负，这说明筋条面积越大，计算值越保守。

5 结 论

(1) 对于薄蒙皮铆接Z型机身加筋板，基于目前的有效宽度计算方法，采用Johnson-Euler方程计算得到的破坏载荷与试验值基本吻合，误差大约在10%之内。

(2) 与试验值对比表明，采用Johnson-Euler方程计算破坏载荷，为了方便，蒙皮有效宽度也可取30ts(材料2024类)。

(3) 几种有效宽度计算方法中，“民机指南”给出的有效宽度最大，计算得到的破坏载荷也最大。这是因为对于薄蒙皮，民机指南中蒙皮有效宽度推导是基于筋条对蒙皮支持为固支，从而导致有效宽度计算公式中的系数从1.9上升为2.4。