具有范数连续性与绝对紧性的双参数有界算子C群的扰动

杨雯雯，庞芙蓉，徐小玲

(1.延安职业技术学院公共教学部，716000，陕西，延安；2. 延安大学数学与计算机科学学院，716000，陕西，延安；3.延安大学西安创新学院，710000，西安)

0 引言

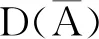
定义1：在空间X上,若双参数有界线性算子簇{S(s,t)}s,t∈R满足以下条件：

1)S(0，0)=C；

2)CS((s1,t1)+(s2,t2))=S(s1,t1)S(s2,t2),∀s1,s2,t1,t2∈R；

3) 映射(s,t)→S(s,t)x强连续，∀s,t∈R;∀x∈X。

则称{S(s,t)}s,t∈R为双参数有界算子C群。

定义2：双参数有界算子C群{S(s,t)}s,t∈R的无穷小生成元是线性算子L:R2→B(X)，定义为：

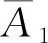
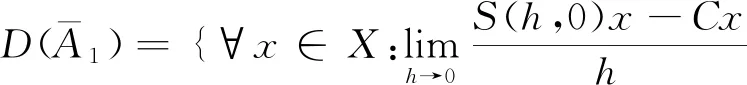
定义3：在空间X上，若双参数有界算子C群{S(s,t)}s,t∈R，满足

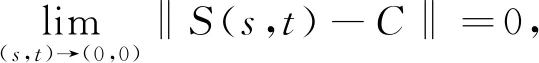
则称双参数有界算子C群{S(s,t)}s,t∈R是范数连续的或具有范数连续性。

定义4：在空间X上，若∀(s,t)∈R2时，双参数有界算子C群{S(s,t)}s,t∈R都是紧的，则称双参数有界算子C群{S(s,t)}s,t∈R是绝对紧的或具有绝对紧性。

引理1：以下2个条件等价：

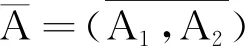
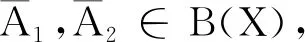
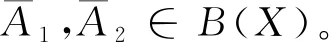
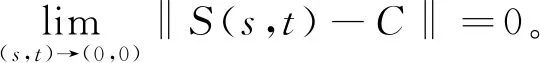
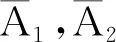
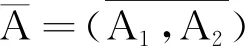
S(s,0)S(0,s)x=S(0,s)S(s,0)x。

由双参数有界算子C群的定义得：

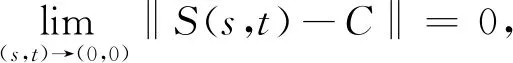
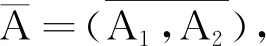
下证{T(s,t)}s,t∈R是范数连续的。

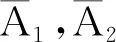
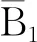
故定理得证。

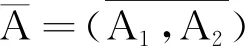
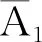
故定理得证。