基于分形理论的接触式机械密封端面摩擦热模拟计算

（南京科技职业学院，江苏省流体密封与测控工程技术研究开发中心，南京 210048）

0 引言

接触式机械密封工作时，由于动、静环密封端面相互贴合并相对滑动，从而产生了摩擦热。摩擦热会引起密封端面温度升高及摩擦系数的变化[1-4]，进而影响机械密封的工作性能和使用寿命[5-7]。过大的端面摩擦热会使密封端面间液膜汽化，造成密封失稳、泄漏量增加，还会加剧端面的磨损和腐蚀，甚至引起热冲击和热裂等。准确计算端面摩擦热是研究机械密封端面温度及密封环温度场分布的基础[8-11]。由于接触式机械密封端面间的实际接触只发生在摩擦面较高的微凸体上，端面的接触特性对端面摩擦热有较大的影响。目前，多数学者[8-10]在计算机械密封端面摩擦热时将端面微凸体简化为顶端曲率半径相同的半球体，微凸体峰高服从于高斯分布，并将微凸体接触简化为弹性或塑性接触。且对密封端面摩擦热影响因素的详细分析研究的较少。

研究表明[12-15]，机械密封端面形貌具有与尺度无关且各向同性的分形特性，且在正常工作参数下，接触式机械密封端面部分接触微凸体处于弹性变形状态、部分处于弹塑性变形状态、部分处于塑性变形状态。本文采用具有尺度独立性的分形参数表征机械密封端面形貌，在已建立的机械密封端面接触分形模型[14]和端面平均温度与摩擦系数计算模型[3-4]的基础上，通过模拟计算分析了工作参数和端面形貌分形参数对接触式机械密封端面摩擦热的影响规律。

1 计算方法

1.1 计算模型

接触式机械密封端面摩擦热的计算式为[1，2，9]：

式中 QF——端面摩擦热，W；

f——密封端面摩擦系数；

pg——密封端面比载荷，Pa，pg=ps+Bp；

ps——弹簧比压，Pa；

B——平衡系数；

p——密封流体压力，Pa；

vm——密封端面平均线速度，m/s；

Aa——密封环带面积，m2；

rm——密封端面平均半径，m；

n——转速，r/min；

r1，r2——密封端面内、外半径，m。

由式（1）可知，要计算密封端面摩擦热首先需求得密封端面摩擦系数。魏龙等[3-4]对接触式机械密封端面摩擦系数与端面平均温度的计算方法进行了研究，推导出了端面摩擦系数f和端面平均温度tm的计算式：

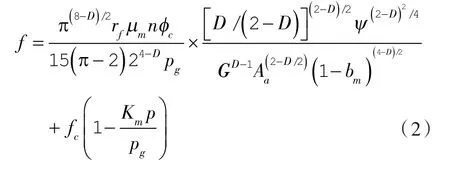
式中 rf——当量摩擦半径，m；

μm——液膜动力黏度，Pa·s；

φc——接触因子；

D——软质环端面分形维数；

G——软质环端面特征尺度系数，m；

ψ——分形区域扩展系数；

bm——密封端面微凸体承载面积比，可由机械密封端面接触分形模型[14]计算得出；

fc——微凸体接触摩擦系数；

Km——膜压系数；

mr，ms——动、静环散热系数，m-1；

λcr，λcs——动、静环材料的等效热导率，W/（m·℃）；

Acr，Acs——动、静环当量筒体轴向横截面积，m2；

Lr，Ls——动、静环当量筒体长度，m；

tf——密封腔内密封流体平均温度，℃。

液膜动力黏度μm可根据密封端面平均温度tm确定。μm与tm之间的关系采用Reynolds黏温公式：

式中 μ0——液膜在温度 t0时的动力黏度，Pa·s；

α——黏温系数，℃-1，对于水α =0.017 5 ℃-1；

接触因子φc可由下式计算[16-23]：

式中χ——膜厚比，表示机械密封端面平均膜厚与端面综合均方根粗糙度的比值。

膜厚比的分形表达式为[3-4]：

式中 lr——实际测量端面形貌时的取样长度，m。

接触式机械密封动、静环端面间处于混合摩擦状态时，膜压系数可按下式计算[14]。

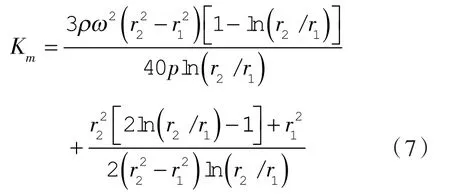
式中 ρ——液膜密度，kg/m3；

ω——角速度，rad/s，ω =πn/30。

密封环简化为当量筒体及散热系数mr，ms的具体计算方法参见文献[3]。

1.2 计算流程

由式（1）～（4）可知，接触式机械密封端面摩擦热QF、摩擦系数f、平均温度tm是相互影响的，具有耦合关系，求解密封端面摩擦热时具体计算流程如图1所示。

图1 端面摩擦热耦合计算流程

2 密封端面摩擦热的影响因素分析

以图2所示的内流式部分平衡型机械密封为例进行计算分析。机械密封动环为镶嵌式硬质环，面环材料为硬质合金YG8，座环材料为301不锈钢；静环为整体式软质环，材料为碳石墨M106K。密封面内直径d1=0.069 m、外直径d2=0.078 m、平衡直径db=0.07 m。密封环简化为当量筒体后的相关参数见表1。密封流体为清水，温度tf=20 ℃。

图2 机械密封结构

表1 密封环当量筒体的相关参数

2.1 工作参数对密封端面摩擦热的影响

2.1.1 弹簧比压ps对端面摩擦热QF的影响

通过模拟计算得到不同密封端面形貌分形维数D和特征尺度系数G组对时，弹簧比压ps对密封端面摩擦热QF的影响如图3所示。计算时，取密封流体压力p=0.5 MPa、转速n=2 900 r/min。

图3 弹簧比压ps对密封端面摩擦热QF的影响

由图3可知，增大弹簧比压ps，则密封端面摩擦热QF线性增大。弹簧比压ps对端面比载荷pg和摩擦系数f有影响。随着弹簧比压ps的增大，摩擦系数与端面比载荷的乘积fpg线性增大，从而引起端面摩擦热线性增大。

2.1.2 密封流体压力p对端面摩擦热QF的影响

通过模拟计算得到不同D和G组对时，密封流体压力p对密封端面摩擦热QF的影响如图4所示。计算时，取弹簧比压ps=0.15 MPa、转速n=2 900 r/min。

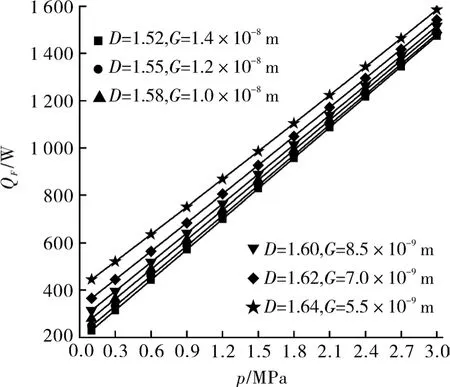
图4 密封流体压力p对密封端面摩擦热QF的影响

由图4可知，增大密封流体压力p，则密封端面摩擦热QF线性增大。密封流体压力p对端面比载荷pg和摩擦系数f有影响。随着密封流体压力p的增大，fpg线性增大，端面摩擦热线性增大。

2.1.3 转速n对端面摩擦热QF的影响

通过模拟计算得到不同D和G的组对时，转速n对端面摩擦热QF的影响如图5所示。计算时，取弹簧比压ps=0.15 MPa、密封流体压力p =0.5 MPa。

图5 转速n对密封端面摩擦热QF的影响

由图5可知，增大转速n，则密封端面摩擦热QF近似呈线性增大，且密封端面越光滑（分形维数D较大、特征尺度系数G较小），摩擦热的增量越大。转速n对端面平均线速度vm和摩擦系数f有影响。随着转速n的增大，端面平均线速度vm成正比增大，而摩擦系数f近似呈线性地增大，且端面越光滑（D较大，G较小）f增大的幅度越大。因此，转速n对密封端面摩擦热QF的综合影响结果是，随着转速n的增大，密封端面摩擦热QF近似呈线性增大，且密封端面越光滑，摩擦热的增量越大。

2.2 端面形貌分形参数对密封端面摩擦热的影响

计算时，取弹簧比压ps=0.15 MPa、密封流体压力p=0.5 MPa、转速n=2 900 r/min。

2.2.1 分形维数D对端面摩擦热QF的影响

通过模拟计算得到密封端面形貌分形维数D对端面摩擦热QF的影响如图6所示。由图6可知，增大密封端面形貌分形维数D，则密封端面摩擦热QF非性线地增大。当分形维数D较小时，密封端面摩擦热QF的变化幅度较小，而且特征尺度系数G值不是太小时其变化对密封端面摩擦热的影响不大；而当分形维数D较大时，随着D增大，QF增大的幅度越来越大。

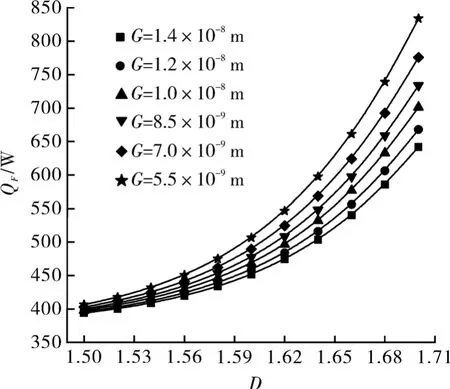
图6 端面分形维数D对密封端面摩擦热QF的影响

分形维数D定量地度量了端面形貌轮廓在所有尺度上的不规则和复杂程度，D越大，轮廓结构越复杂，轮廓细节越丰富，轮廓曲线幅值也越小，因而端面越光滑。随着分形维数D的增大，密封端面间实际接触面积增大、平均膜厚减小、摩擦系数增大，从而加剧了端面间的摩擦，引起端面摩擦热QF非性线地增大。当D较小时，端面较粗糙，端面间实际接触面积很小、平均膜厚较大，端面间接近于流体摩擦状态，因此，端面摩擦热QF变化幅度较小；而且G值不是太小时其变化对端面粗糙度影响较小，因此，对密封端面摩擦热QF的影响也不大。当D较大时，端面较光滑，且随着D的增大，平均膜厚减小，端面间微凸体接触摩擦的比例迅速增大，端面摩擦热QF增大的幅度越来越大。

2.2.2 特征尺度系数G对端面摩擦热QF的影响

通过模拟计算得到密封端面形貌特征尺度系数G对端面摩擦热QF的影响如图7所示。计算时，取弹簧比压ps=0.15 MPa、密封流体压力p =0.5 MPa、转速 n=2 900 r/min。

图7 端面特征尺度系数G对密封端面摩擦热QF的影响

由图7可知，减小特征尺度系数G，则密封端面摩擦热QF非性线地增大。当特征尺度系数G较大时，密封端面摩擦热QF的变化幅度较小，而且分形维数D值不是太大时其变化对密封端面摩擦热的影响不大；而当特征尺度系数G较小时，随着G减小，QF增大的幅度越来越大。

特征尺度系数G的大小不影响端面形貌轮廓的横向间距和微凸体的数量，而只影响轮廓幅值的大小，当G增大时，轮廓曲线幅值随之增加，导致表面轮廓高度均值增大，因而表面变得越来越粗糙，即G增大使凸峰变的更高，凹谷变的更深。随着特征尺度系数G的减小，密封端面间实际接触面积增大、平均膜厚减小、摩擦系数增大，从而加剧了端面间的摩擦，引起端面摩擦热QF非性线地增大。当G较大时，端面较粗糙，端面间实际接触面积很小、平均膜厚较大，端面间接近于流体摩擦状态，因此，端面摩擦热QF变化幅度较小；而且D值不是太大时其变化对端面粗糙度影响较小，因此，对密封端面摩擦热QF的影响也不大。当G较小时，端面较光滑，且随着G的减小，平均膜厚减小，端面间微凸体接触摩擦的比例迅速增大，端面摩擦热QF增大的幅度越来越大。

3 结论

（1）接触式机械密封端面摩擦热、摩擦系数、端面温度是相互影响的，具有耦合关系。本文提出的密封端面摩擦热耦合计算方法揭示了密封端面摩擦热与机械密封工作参数、结构参数、密封端面形貌分形参数之间的关系。该方法的建立，为计算机械密封端面摩擦热提供了基础。

（2）密封端面摩擦热受机械密封工作参数的影响较大。随着弹簧比压或密封流体压力的增大，密封端面摩擦热线性地增大；随着转速n的增大，密封端面摩擦热近似呈线性增大，且密封端面越光滑，摩擦热的增量越大。

（3）密封端面形貌也是影响端面摩擦热的关键因素。随着端面分形维数D的增大或特征尺度系数G的减小（密封端面光滑程度增大），密封端面摩擦热非性线地增大；当分形维数D较小、特征尺度系数G较大时，密封端面摩擦热QF的变化幅度较小；而当D较大、G较小时，随着D增大、G减小，QF增大的幅度越来越大。