VRF制冷系统频率与阀开度同步控制模型与试验验证

（上海理工大学 制冷与低温工程研究所，上海 200093）

0 引言

随着我国建筑业的蓬勃发展，变制冷剂流量（VRF）空调技术因其具有软启动、快速制冷、温控精度高等特点，得到了广泛的应用和快速的发展[1]。压缩机频率与电子膨胀阀开度作为空调系统中控制的主要元件[2]，其变化直接影响着系统的稳定与性能，对两者的研究一直是研究的热点。

在频率方面，石毅登等[3]提出变频技术具有高效、节能和控温精度高等优点，为变频技术应用在制冷系统中奠定了基础。赵力等[4]对压缩机频率与压缩机功耗、COP等参数之间的关系进行了理论和试验研究，根据试验数据得到它们之间存在某种规律。伍光辉等[5]建立了制冷量和压缩机频率的关系方程，得到了较好的系统优化效果，但控制策略还不够全面。赵瑞昌等[6]等通过试验分析不同高（低）温级压缩机频率下系统的性能变化，得到在高（低）温级压缩机频率为53 Hz时，系统复叠温差最小，系统COP最优。

在阀开度方面，章晓龙等[7]得出电子膨胀阀的最小稳态过热度曲线，并在动态响应试验中得出蒸发器增益与时间常数、延迟时间与蒸发温度和过热度的关联性，为电子膨胀阀的控制优化提供参考。虞中旸等[8]以空气源热泵热水器试验系统为研究对象，通过改变电子膨胀阀开度，研究不同调节方式对系统性能的影响，提出了以压缩机吸气过热度为控制对象调节电子膨胀阀的方法。袁朝阳等[9]利用电子膨胀阀调节灵活的特性，对空气源热泵热水器在定阀开度和定过热度下的系统性能做了对比试验，并提出了电子膨胀阀的排气温度控制法。彭喜姣[10]对电子膨胀阀在定频制冷系统上的应用进行了研究，得出可以减小了压缩机的频繁启动，延长了压缩机的使用寿命。陈文俊[11]介绍了3种热水机电子膨胀阀的控制方式，指出3种方式各自的优缺点和适用范围。

在频率与阀开度方面，侯泽飞[12]等从理论上总结了频率变化与电子膨胀阀开度的关系，并指出二者应匹配调整，才能得到最佳的制冷效率。由玉文等[13-14]提出了压缩机频率和电子膨胀阀开度协调控制方法。此方法虽控制精度高，但需先通过对电子膨胀阀的控制而产生各参量的扰动，再控制压缩机做出相应的调节，很容易会产生延迟或超调现象[15]，使系统在短期内难以达到稳定。吴东兴等[16]总结多联式空调（热泵）机组电子膨胀阀和压缩机的一般控制方案的基础之上，提出了新的控制方法：电子膨胀阀——压缩机的同步控制，并以具体的电子膨胀阀和压缩机为例说明了此方案的具体实施过程。故本文希望通过试验研究，得到系统电子膨胀阀开度与压缩机频率的同步控制模型，使系统可以达到迅速稳定，实现精确控制，降低控制难度。

1 试验装置与方法

1.1 试验装置

试验装置为一台小型变流量制冷系统，循环原理如图1所示。

图1 试验装置原理

本试验台采用以R32为制冷剂运行的变频滚动转子式压缩机，自带气液分离器，其理论排气量为10.2 mL/r，频率可以在16.6～120 Hz之间变化，压缩机的额定功率为50 Hz。

系统中制冷剂的质量流量m采用科氏力串联管型流量计测量，单位为g/s，量程范围为0.05～2.5 kg/min，测量精度为±0.1%。冷冻水循环和冷却水循环都装有一个浮子流量计，可测的体积流量qv，单位为mL/s。温度采用允许偏差±0.15 ℃+0.002|t|的内嵌式铂电阻测量，其中t表示测量温度，单位为℃。压力采用精度为0.5%，量程为0～40 MPa的压力变送器测量。

电子膨胀阀采用步进电机驱动，可通过手动调节控制器来改变其开度。总步数为2 500步，可以精确地调节制冷剂流量。

1.2 试验方法

国内空调标准工况蒸发温度为7.2 ℃，冷凝温度为54.4 ℃。为了模拟常规空调运行工况，以及考虑到蒸发侧与冷凝侧的换热温差，本文将冷冻水出水温度设置为7 ℃，冷却水出水温度为39 ℃，过冷度保持在7 ℃。同时设置对照组冷冻水出水温度为10 ℃，冷却水出水温度不变，以保证试验的准确性。具体试验工况如表1所示。

表1 试验工况 ℃

变流量制冷系统主要通过压缩机频率或电子膨胀阀开度来改变流量，故本文分别进行定频率变阀开与定阀开变频率2组不同的试验，得到频率与阀开度之间的关系。具体步骤如下：

（1）以额定频率50 Hz启动压缩机，调节电子膨胀阀开度，使蒸发器出口过热度稳定在10 K附近，运行60 min以上，之后将电子膨胀阀开度逐步增大，使过热度稳定地下降到9 K，依次分别记录过热度在到达8，7，6，5，4，3，2，1 K时所需数据。为保证数据准确性，在达到一个过热度时，使系统稳定运行60 min后，记录10 min内数据并取平均值。

（2）提升压缩机频率至55 Hz运行，在工况1/2下，将电子膨胀阀开度定为600/782步，使蒸发器出口过热度稳定在10 K附近。降低压缩机频率使蒸发器出口过热度稳定地下降到9 K，依次分别得到过热度在到达 8，7，6，5，4，3，2，1 K 时所需的数据。为保证数据准确性，在达到一个过热度或吸气干度时，使系统稳定运行60 min后，记录10 min内数据并取平均值。

1.3 计算公式

由试验所测得的数据，并通过Rrefprop9.0软件可以得到蒸发器出口压力Pe对应的制冷剂饱和液态焓he,l、饱和气态焓he,v和饱和温度Te,sat，系统质量流量m。

蒸发器出口过热度：

式中 Tsh——蒸发器出口过热度，K；

Te——吸气温度，K；

Te,sat——蒸发压力下的饱和温度，K。

2 试验结果与分析

2.1 工况1下频率与阀开度的同步控制拟合

图2示出工况1下电子膨胀阀开度对质量流量的影响图，随着阀开度的增大，质量流量是逐渐增大的，阀开度越大对质量流量影响越明显。虚线为拟合曲线，拟合公式如下：

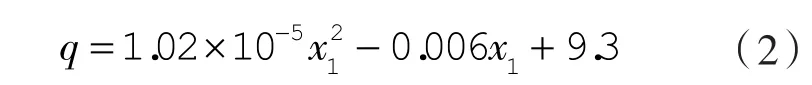
式中 q——质量流量，g/s；

x1——工况1下吸气过热状态电子膨胀阀开度。

此外，为得到最佳拟合度，提高控制精度，将电子膨胀阀开度与质量流量采用二项式拟合，拟合因子R2为0.997 42。

图2 工况1下电子膨胀阀开度对质量流量特性曲线

图3示出工况1下频率对质量流量影响，从图中可以看出，随着频率的逐渐增大，质量流量是逐渐增大的。虚线是工况1下频率与质量流量的拟合曲线，拟合式如下：

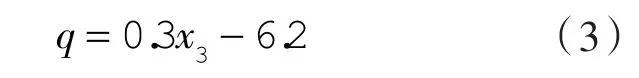
式中 x3——工况1下的频率，Hz。

此外，为保证较最佳拟合效果，提升控制精度，将频率与质量流量采用一次函数拟合，拟合因子 R2为 0.999 51。

联立式（2）和（3）可得工况1下频率与电子膨胀阀开度的关系式：

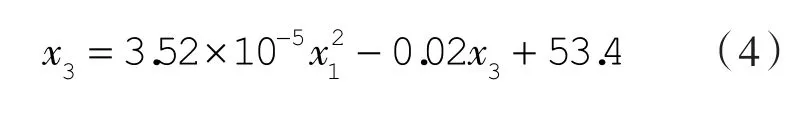
图3 工况1下频率对质量流量特性曲线

2.2 工况2下频率与阀开度的同步控制拟合

图4示出工况2下电子膨胀阀开度对质量流量的影响，随着阀开度的增大，质量流量是逐渐增大的，阀开度越大对质量流量影响越明显。

虚线为拟合曲线，拟合公式如下：

式中 x4——工况2下吸气过热状态电子膨胀阀开度。

此外，为得到最佳拟合度，提高控制精度，将电子膨胀阀开度与质量流量采用二项式拟合，拟合因子R2为0.995 64。

图4 工况2下电子膨胀阀开度对质量流量特性曲线

图5示出工况2下频率对质量流量影响，从图中可以看出，随着频率的逐渐增大，质量流量是逐渐增大的。虚线是工况2下频率与质量流量的拟合曲线，拟合公式如下：

式中 x6——工况2下的频率，Hz。

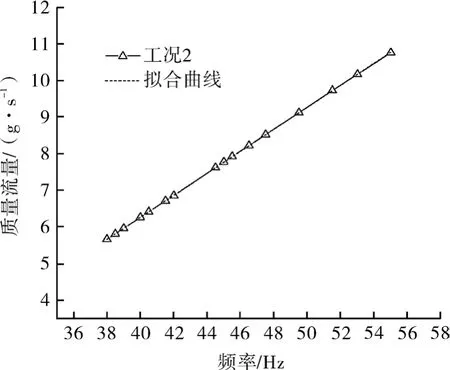
图5 工况2下频率对质量流量特性曲线

此外，为保证较最佳拟合效果，提升控制精度，将频率与质量流量采用一次函数拟合，拟合因子 R2为 0.999 99。

联立式（5）和式（6）可得工况2下频率与电子膨胀阀开度的关系式：

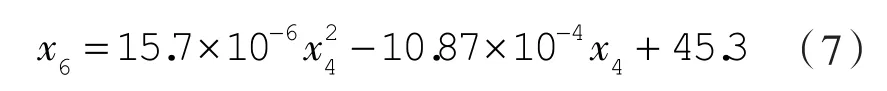
在工况1的条件下，可以得到电子膨胀阀开度与频率之间的关系为式（4）；在工况2的条件下，可以得到电子膨胀阀开度与频率之间的关系为式（7）。对比式（4）和式（7），当工况发生变化时，频率与电子膨胀阀开度的对应关系式也会改变，故需研究在不同工况下的同步控制模型。在系统达到稳定之前，可以根据同步控制模型进行调整，能有效减少系统频繁调节所引起的超调或延迟现象。

3 频率与阀开度同步调节模型

系统制冷剂质量流量直接影响着系统的性能，它与电子膨胀阀开度OEEV（Open of Electronic Expansion Valve），压缩机频率f和蒸发温度Te有关。

电子膨胀阀开度OEEV与质量流量关联式在文献[17-18]中采用水力学形式来描述：

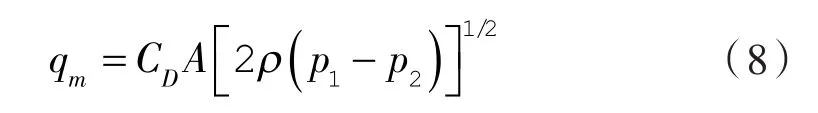
式中 qm——制冷剂的质量流量；

CD——流量系数；

A——电子膨胀阀的流通截面积；

ρ——电子膨胀阀入口制冷剂的密度；

p1——电子膨胀阀前制冷剂入口压力；

p2——电子膨胀阀后制冷剂出口压力。

但该方程与电子膨胀阀实际流动特性有较大的差别，故研究大都集中在对CD的经验关联式上[19]。

针对压缩机频率f，在文献[20]中提出转速n是定子电源频率的正比例函数，故和系统质量流量也有一定关系。

对于蒸发温度Te来说，它与冷冻水温度有关，冷冻水温度越低，蒸发温度越低。而系统冷媒的流量减小也可降低蒸发温度。

针对以上分析并结合式（2）和式（3）可以得出，qm与OEEV成二次项关系式，qm与f成一次项关系式。故建立如下关系式：

式中 ɑ0，ɑ1，…，ɑ14——常数；

O——阀开度。

采用图2～5中的数据对式（9）进行计算得出系数，具体见表2。

表2 拟合系数值

4 拟合结果试验验证

为验证该关系式的正确性和适用性，设计新工况进行验证。设定压缩机频率50 Hz下冷冻水/冷却水出水温度7/37 ℃和冷冻水/冷却水出水温度11/37 ℃，改变电子膨胀阀开度，使压缩机吸气口过热度由10 K降到1 K。以及设定电子膨胀阀开度为840步，冷冻水/冷却水出水温度11/37 ℃，压缩机频率由55 Hz开始下降，使吸气口过热度由10 K降到1 K。

图6示出了3个工况下系统质量流量实际值与计算值的对比。结果显示，系统质量流量模型计算值与试验值最大相对误差为3.99%，最小相对误差为0.04%，因此计算值与实际值基本吻合，该模型较为可靠。另外，质量流量最大相对误差出现在定阀开变压缩机频率的工况下，即此种工况下模型误差相对较大。观察图6（a）、（b），不难发现当电子膨胀阀开度越小时，计算值与实际流量偏差越来越大，且随着阀开度的增大，计算值均在实际值附近波动。对于图6（c）来说，起始频率时计算值在实际值附近波动较大，随着频率的提升，波动越来越小，故该模型更加适用于频率较大的工况。

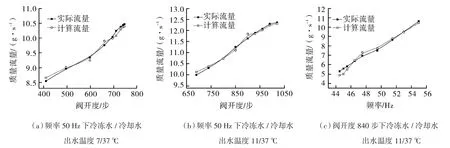
图6 3种工况下系统质量流量实际与计算值的对比

5 结论

（1）质量流量随电子膨胀阀开度的增大呈二次项增加趋势，且阀开度越大对质量流量影响精度越高；质量流量与压缩机频率几乎与成线性增长，压力、密度等其它因素影响相对较小。

（2）以系统质量流量为控制目标，建立了压缩机频率与电子膨胀阀开度的同步控制模型，经试验验证，计算值与实际值的最大相对误差为3.99%，最小相对误差为0.04%，因此该模型具有较好的可靠性。

（3）在控制系统质量流量时，均可得到对应流量下的频率、阀开度与蒸发温度值，以此为变量便可建立同步控制模型，可以使试验台在运行初期迅速达到稳定，无需频繁调节控制元件，在节省时间的同时延长了器件的使用寿命。

本文提出的同步控制模型主要针对的是压缩机吸气口过热态，而压缩机吸气口带液态可提高系统COP，也需要进行模型建立和试验验证。另外，压缩机带液过量可能造成液击现象，如何合理控制带液量，这在今后的研究中需要重点关注。