链传动纵向动力学研究

□ 喻文广

上海电气集团股份有限公司 中央研究院 上海 200070

1 研究背景

在链传动过程中,由于链轮和链条啮合过程中存在多边形效应,加之周期性冲击载荷的作用,导致链传动发生横向、纵向振动[1-13]。其中,链条纵向振动将对链条运动的同步性与均匀性有较大影响,且对运动平稳性的影响要大于横向振动。对于装有纵向导轨的链传动,如自动扶梯梯级链、步进链而言,横向振动可以忽略。

对于链条纵向振动问题,早在20世纪90年代,国内学者就开始了相关研究,主要采用能量法对链传动系统进行简化,建立少量自由度的模型,推导出相应纵向振动方程,给出纵向振动频率的解析解[8-11]。近十年,很多学者建立了更复杂的纵向振动模型,并应用有限单元法将链条离散化为若干彼此相连的纵向杆单元或者弹簧单元组合体,采用数值解法分析纵向动力学特性[12-13]。最近几年,随着多体动力学的发展,开始出现少量基于多体动力学理论建立链传动系统复杂动力学模型的相关研究[14]。目前,在这些链传动纵向振动的研究中,关于松边链条对振动的影响及链条纵向振动模型边界问题的研究都较少,而这些都是影响动力学分析结果的重要因素。

笔者以长节距滚子链为对象,建立纵向振动力学模型,研究链条边界问题的处理,并考虑松边链条质量对振动的影响,计算链条纵向振动频率。对链条纵向振动开展试验对比分析,根据试验结果对链条振动模型进行参数修正,并基于修正模型分析工作段链条长度对振动频率的影响。

2 动力学模型

2.1 滚子链一般形式

为了使研究的问题更具有一般性,建模时忽略链条导轨形状、链条形状和数量,以及主从动链轮齿数差异等因素,以链条运动为主要特征,将滚子链描述为一般结构形式,如图1所示。图1中,m为链条链节的等效质量,J1、J2为主从链轮的惯量,R1、R2为主从链轮的半径。

由于链条全程都受导轨支撑和约束,因此链轮在多边形效应作用下的纵向振动问题是影响系统性能的主要因素。

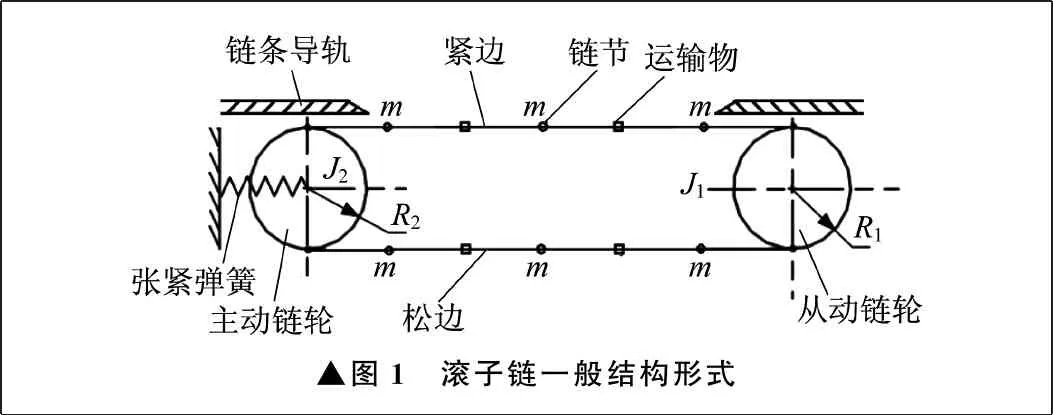
▲图1 滚子链一般结构形式

2.2 纵向动力学建模

链条是由相同链节以铰链形式连接起来的一种柔性体,在进行动力学建模及分析过程中,引入如下四条假设:

(1) 链条紧边始终绷紧在一条直线上,附有纵向导轨约束,忽略横向振动;

(2) 由于紧边与松边张力差别很大,因此仅考虑松边质量的影响,忽略松边刚度的影响;

(3) 将链条简化为张紧的弹簧振子系统,链条及链节质量缩聚在节点上;

(4) 链轮是理想的无偏心轮。

依据功能原理,将主从动链轮转动惯量J1、J2的等效质量分别记为m1、m2,等效到链条与主从动链轮的切点上。由于松边两端分别连接在主从动轮上,因此其质量与主从动轮一起参与链路的振动,影响系统的动力学特性。将松边质量分别等效到主从动链轮上,随同主从动链轮质量一起记为M1、M2,等效到链条与链轮的切点上。由于松边链条由从动轮啮入,被主动轮送出,因此将松边质量全部计入从动轮边。有如下关系式:

(1)

应用有限元法将链条离散为若干个刚度为k的弹簧振子系统组合体,将链节和输运质量等效附加在节点处。对于链条而言,链轮系统是链条两端的边界,因此将主从动轮及张紧器分别沿纵向运动方向等效为两个纵向弹簧,刚度分别记为K1,K2,作为链条两端的弹性支撑边界。

根据以上假设及等效,最终可建立链传动纵向动力学模型,如图2所示。

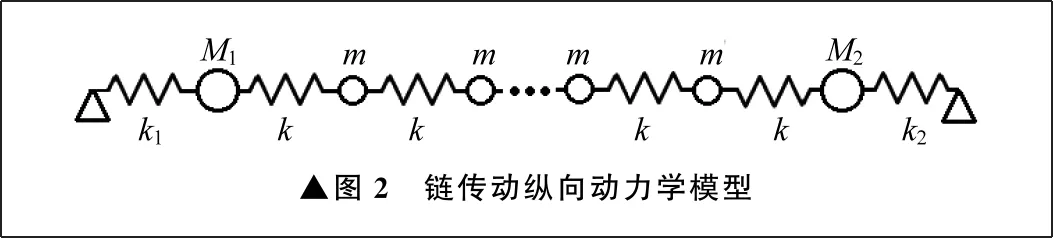
▲图2 链传动纵向动力学模型

2.3 多边形效应

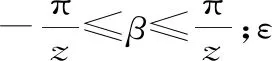
多边形效应如图3所示。由于多边形效应的作用,会使链条速度发生周期性波动,作用在链条上的力也会发生周期性变化。在运动过程中,啮合点沿纵向运动方向的速度v、加速度a及作用力F为:

v=Rωcosβ

(2)

=R(εcosβ-ω2sinβ)

(3)

F=ma

(4)

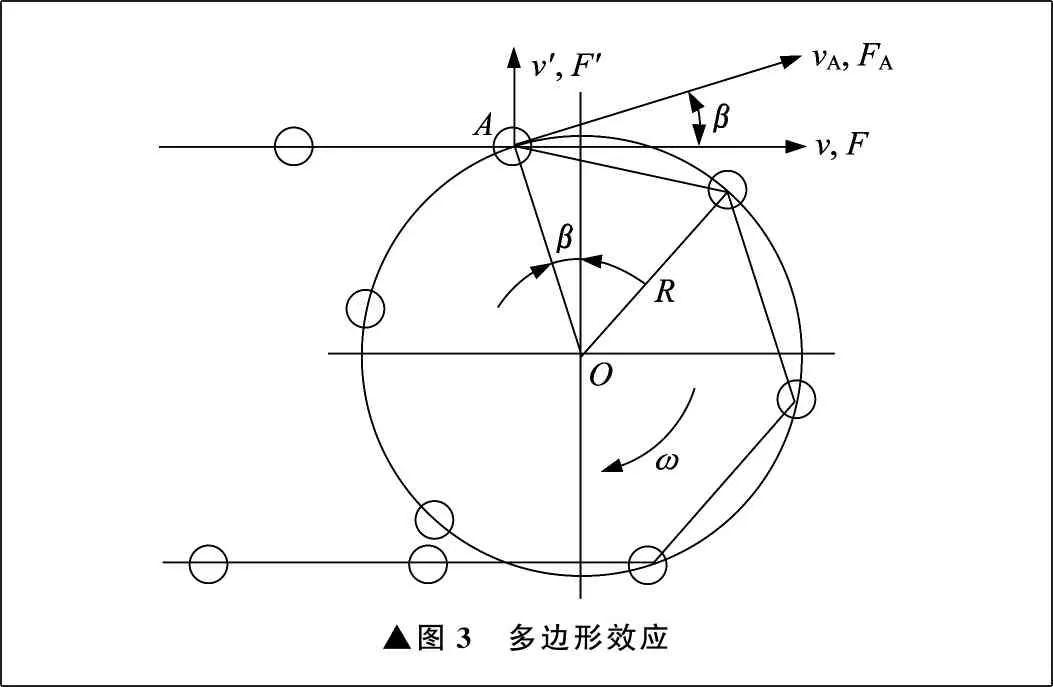
▲图3 多边形效应

3 动力学方程

设紧边链有n个链节,链节距为l,链板截面积为A,链节质量为m,链条刚度为k,取链节点各自微小的偏离平衡位置的纵向位移u1,u2,…,un为系统的广义坐标,将单元质量组集扩展后,得到系统的(n+1)×(n+1)阶总质量矩阵M为:

(5)

同理,可以得到系统的(n+1)×(n+1)阶总刚度矩阵K为:

(6)

链条刚度k为:

k=-EA/l

(7)

式中:E为材料的弹性模量。

系统广义力n+1列列阵F为:

(8)

由此可得整个系统的最终总动力学方程为:

(9)

式中:U为位移矩阵。

4 分析结果

工作段链条长度为9 m,链条节距为100 mm,链条额定运行速度为0.6 m/s,基于上述模型,对链条动力学及链条的刚度进行计算,均采用有限元法求解和分析。

4.1 链条刚度及边界刚度

链条在运行过程中主要承受拉伸作用,所以链条的刚度为拉伸刚度。对于主动链轮而言,除质量和转动惯量外,对系统动力学特性影响最大的因素就是扭转刚度。

由于链轮为链条的支撑边界,且所建立的链传动模型仅考虑纵向运动,因此将链轮扭转刚度的效应等效至链轮链条啮合点处的纵向刚度,即边界支撑刚度k1。对于从动轮等效刚度k2,由于从动轮连接弹簧张紧器,因此计算时需要串联张紧弹簧的刚度。

4.2 系统纵向振动频率及响应

计算表明,链传动系统的纵向振动一阶频率为6.3 Hz,二阶频率为20.7 Hz,频率响应曲线如图4所示。在现有链条运行速度下,链轮啮合频率为6 Hz,系统纵向频率与啮合频率过于接近,可能导致链条发生纵向共振问题。

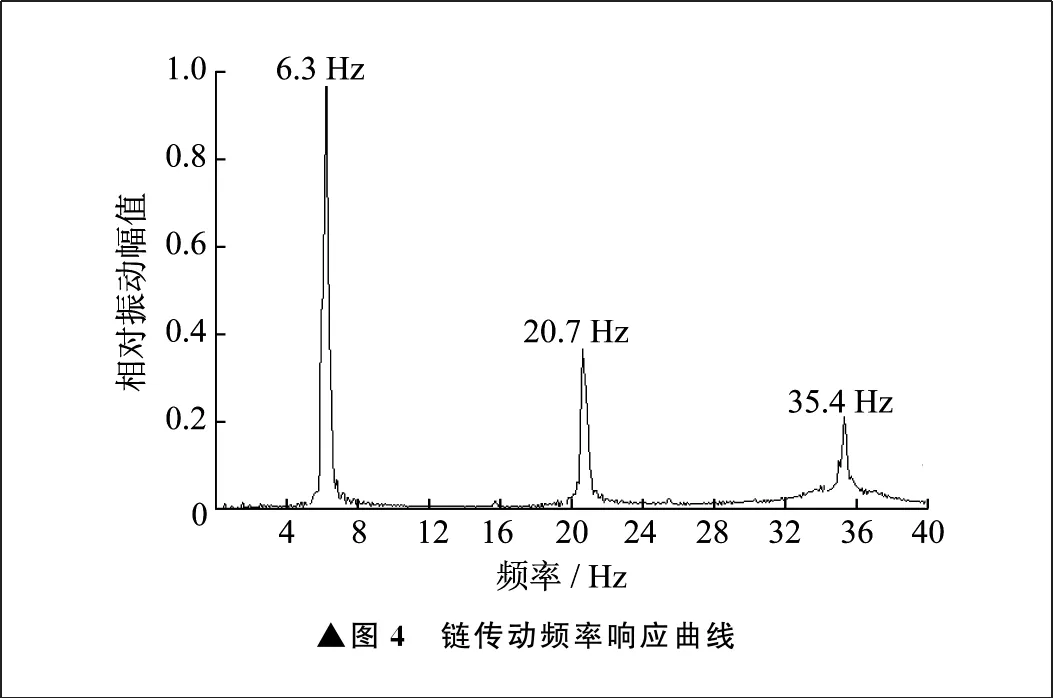
▲图4 链传动频率响应曲线

同时对链传动从启动到平稳运行的过程进行瞬态响应分析,结果如图5所示。随着链轮运行速度的加快,多边形效应的激励增大,链节振动响应幅值也随之增大。当运行到2 s后,振动响应幅值达到最大,此时链条运行速度接近额定速度0.6 m/s,对应多边形效应的激励频率约为6 Hz。

▲图5 链传动启动过程瞬态响应曲线

5 试验

链传动动力学试验时,将信号采集装置固定于链节处,采集链节的振动加速度信号。为了获取链条准确的纵向振动频率,在一定范围内对不同运行速度下的试验结果进行分析。不同运行速度和激励频率下纵向振动加速度如图6所示,可以看出随着激励频率提高、运行速度加快,链节处纵向振动加速度幅值增大。当激励频率达到约6 Hz,运行速度达到约0.6 m/s,纵向振动加速度达到最大值。激励频率继续提高,相对振动加速度幅值减小。所以6 Hz为链纵向共振频率点,即运行速度为0.6 m/s时链条发生纵向共振。

画卷内容深刻，绝不是一个方面可以涵括，一首题画诗会有多方面的品评。 以上六类常常交错融合，不同程度地表现在题咏上。

▲图6 不同运行速度和激励频率下振动加速度

为了进一步研究链传动的动力学特性,选取链条运行速度为6 m/s时的工况进行分析,对加速时域信号进行快速傅里叶变换后,获取振动加速度响应频域曲线。一阶和二阶频率试验与分析结果对比见表1,可见试验结果与分析结果基本一致。

表1 频率试验结果与分析结果对比

系统前两阶频率试验结果比分析结果低,一阶频率低5%,二阶频率低10%,原因可能有两方面。第一是在轮齿啮合过程中,由于接触效应存在接触刚度,导致实际边界刚度要比计算的刚度值低。第二是目前关于链轮系统等效刚度的计算及松边质量分配并无准确分析方法,所以在等效计算过程中存在一定误差。根据试验结果,分别对链轮等效边界刚度及松边质量等参数进行适当修正,将修正后的模型应用于其它长度链条的动力学分析。

6 链条长度对振动的影响

基于修正后的模型,对工作段链条长度对链传动动力学特性的影响进行分析,分别分析长度为7 m、9 m、11 m、13 m、15 m的链条的纵向振动频率,结果如图7所示。

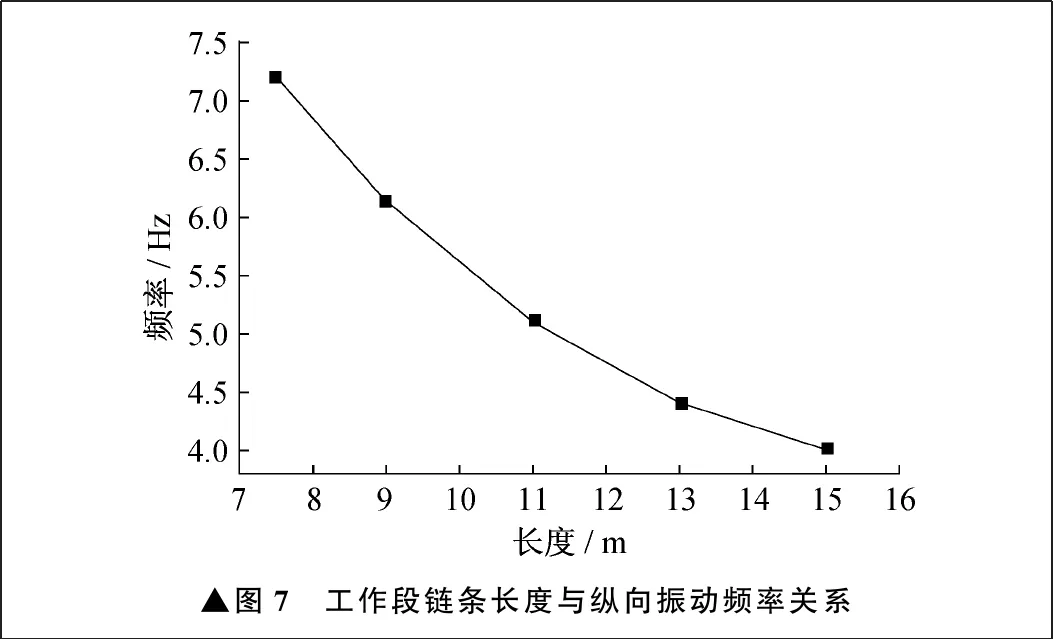
▲图7 工作段链条长度与纵向振动频率关系

由图7可见,链条频率随着链条长度的增大而降低,但是降低幅度并非与长度增大成线性关系。随着长度的增大,单位长度下频率的降幅减小。

笔者分析的链传动系统,其工作转速一般为0.6 m/s左右,此链条节距下对应多边形效应激励频率为6 Hz,而工作段链条设计长度为10 m时链条的结构纵向频率为5 Hz左右,恰处于共振区间。按照结构频率避开激励频率±10%的原则,当工作链条长度为9.25～11.75 m时,需要考虑纵向共振问题,并采取一些避振措施,如调整链条节距从而改变多边形激励频率,或者调整链条刚度、质量以调整纵向频率。

7 结束语

笔者建立了滚子链传动纵向动力学分析模型,讨论了链条边界问题的处理,并考虑了松边质量的影响,采用有限元方法分析了链传动纵向动力学特性,进行试验对比分析。

分析结果与试验结果吻合良好,结果表明链条长度在10 m左右时会引发结构共振问题。在后续设计过程中,需要调整相关结构参数以避免共振。

链条模型的边界问题是影响分析结果的重要因素,建模分析时需要考虑边界问题的处理。

笔者建立的滚子链纵向动力学分析模型,对于链传动问题具有一般性,可应用于其它型号滚子链的振动问题分析中。

链传动系统是一个较为复杂的系统,笔者在建模过程中忽略了链轮啮合接触刚度等因素,对于某些问题的分析处理,如松边质量分配、链轮等效刚度分析等,需要在后续研究中进一步深入完善。