双十字万向联轴器对船舶轴系振动影响的分析*

□ 牛雨生 □ 董良雄 □ 温小飞 □ 周文强

浙江海洋大学 船舶与机电工程学院 浙江舟山 316022

1 研究背景

船舶动力装备是船舶的心脏,其中,船舶推进轴系是船舶动力装备的核心部分,船舶推进轴系的稳定运行是保证船舶安全工作的基本前提。在实际航行过程中,船舶航行环境错综复杂,在遭遇搁浅、碰撞等情况时,推进轴系将会产生不同程度的振动及损伤,进而造成传动零件损坏、轴承过度磨损,甚至轴系断裂等事故,直接影响船舶航行性能和安全性。由此,对船舶推进轴系的振动进行研究,一直是热点问题[1-4]。

联轴器作为连接船舶主机与轴系的关键部分,具有较强的角补偿能力,能够实现平稳传递扭转力矩。近年来,国内外学者围绕联轴器进行了一些理论研究。Mazzei等[5]研究了由万向联轴器主动轴和从动轴组成的系统的动稳态性。高治华等[6]对十字轴式万向联轴器的运动进行了仿真分析。 汪自强[7]以内燃机轴系为研究对象,分析联轴器对轴系扭振的影响,并进行了减振研究。彭涛[8]对考虑弹性联轴器的船舶轴系耦合振动特性进行了分析。徐翔等[9]基于MATLAB软件,对万向联轴器进行了非线性扭振仿真。在联轴器传递扭矩的过程中,只要主动轴和从动轴之间存在一定的夹角,那么即使主动轴转速恒定,从动轴也会产生转速波动,同时也会产生二次激励[10-11]。但是,夹角大小对轴系振动产生影响的规律,目前还没有太多相关研究。对此,笔者以联轴器和船舶轴系为研究对象,对联轴器与轴系的耦合性进行分析,研究轴线夹角对轴系振动的影响。

2 双十字万向联轴器基本扭振分析

双十字万向联轴器可看成由两个单万向联轴器和一根中间轴组成,考虑到中间轴较长,加之自身扭转刚度和扭转阻尼的影响,将中间轴离散为两个转动惯量相等的惯性圆盘,建立如图1所示双十字万向联轴器当量模型。

双十字万向联轴器的动能Ep为:

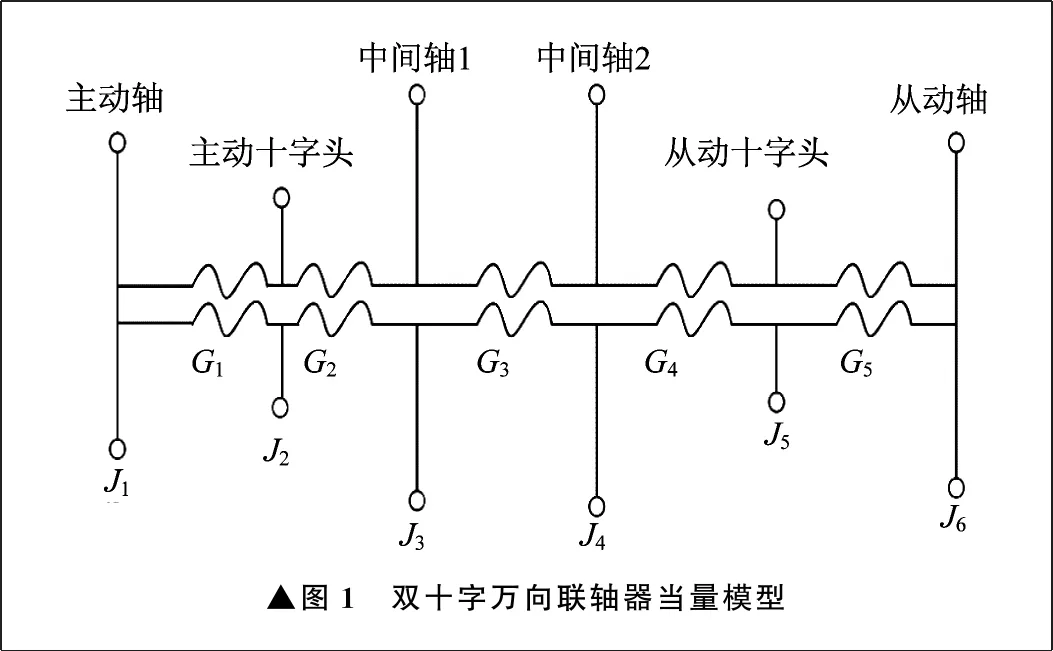
▲图1 双十字万向联轴器当量模型

(1)

势能Ev为:

Ev=[G1(θ1-θ2x)2+G2x(θ2x-θ3cosβ1)2

+G2y(θ2y-θ3sinβ1)2+G3(θ3-θ4)2

+G4y(θ4cosβ2-θ5x)2+G4x(θ4sinβ2-θ5y)2

+G5(θ5x-θ6)2]/2

(2)

将式(1)和式(2)代入第二类拉格朗日方程,建立运动微分方程组:

(3)

(4)

(5)

(6)

(7)

(8)

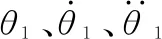
设定双十字方向联轴器的初始参数如下:J1=J6=4.8 kg·m2,J2x=J5x=2 kg·m2,J2y=J5y=1.2 kg·m2,J3=J4=8.8 kg·m2,G1=G2x=G2y=G3=G4x=G4y=G5=2×107N·m/rad。

改变β1、β2的大小,取β1=β2=1°、β1=β2=5°、β1=β2=8°,在MATLAB软件中进行数值仿真,对双十字万向联轴器从动轴进行分析,转角响应曲线如图2所示。0～0.02 s时,三种工况下的曲线都可看作由两个循环周期组成,转角响应曲线有明显波动,可以认为由式(3)～式(8)中复杂的三角函数所引起。每个循环周期出现了不同的峰值,其中β1=β2=5°时转角最大,峰值大小随β1、β2先增大后减小,说明轴线夹角大小对联轴器扭振有不可忽略的影响。在三种工况下,随着时间的延长,循环周期逐渐增加,同时复杂三角函数所引起的波动越来越强。最终系统趋于稳定,所有转角响应曲线呈拟周期变化。三种工况下的计算结果表明,在合理的范围内改变轴线夹角,不会破坏联轴器的自身稳定性,但轴线夹角的大小会影响转角,选择合适的轴线夹角有利于联轴器传递扭矩。

3 双十字万向联轴器与轴系耦合性分析

双十字万向联轴器从动轴与轴系相连接,当联轴器从动轴受到来自轴系的横向力时,将造成联轴器夹角变化,进而产生联轴器和轴系的耦合振动。忽略复杂结构,对轴系耦合模型进行简化,如图3所示。

图3中,实线A代表双十字万向联轴器的初始位置,实线B代表双十字万向联轴器受到横向激振力后的位置。在横向力的作用下,夹角β变化为β′。L为

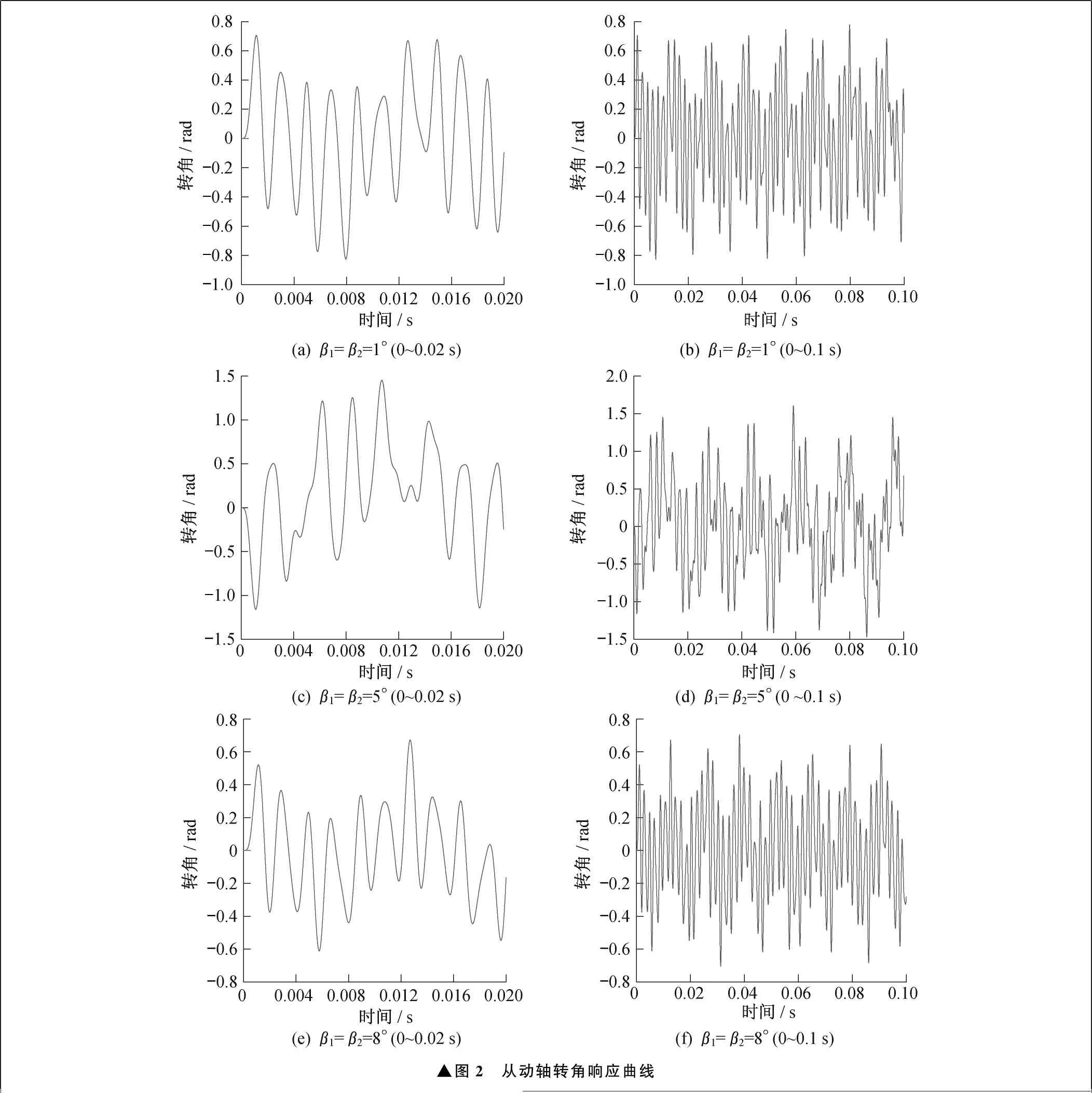
▲图2 从动轴转角响应曲线

▲图3 轴系耦合简化模型

联轴器主动轴和从动轴的长度,H为垂直距离,M为轴系横向力矩。

根据图3模型及材料力学原理,有:

(9)

式中:EI为抗弯刚度;ω为激振力频率;t为时间。

假设联轴器从动轴所受横向力矩M与扭矩T为同一数量级,T=M=18 000 N·m,选取β=1°、β=8°、ω=3 600 (°)/s,根据式(9)进行计算,可得到β′随时间变化曲线,如图4所示。

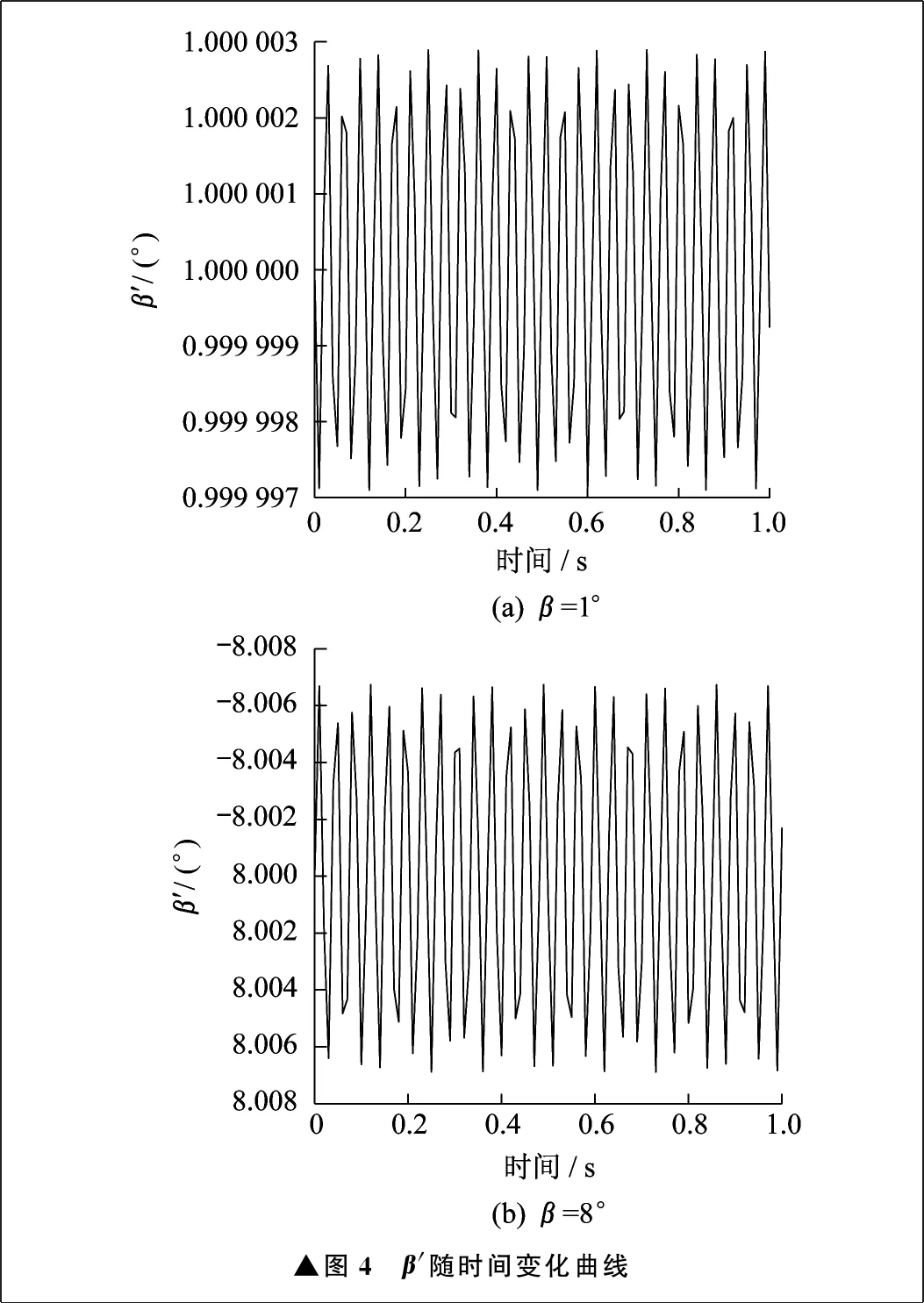
▲图4 β'随时间变化曲线

由图4可以看到,在轴系对联轴器从动轴施加弯矩的情况下,联轴器夹角有明显的幅度变化。对于不同的初始角度,夹角变化曲线有相似波动规律,可以认为横向力在两种情况下作用的方式相同。同时,初始夹角越大,横向力作用的结果越明显,说明轴系力矩对联轴器产生振动影响,导致夹角发生变化。

4 双十字万向联轴器轴线夹角影响分析

通常情况下,双十字万向联轴器中十字轴的转动惯量与其它器件相比,可忽略不计。中间轴较长,可分为两个部分,同时不考虑内部阻尼力,建立不考虑十字头的联轴器当量模型,如图5所示。

采用第一类拉格朗日方程,有:

(10)

为了分析双十字万向联轴器轴线夹角变化对轴系振动产生的影响,将轴系离散化为一个集中质量的圆盘,两端为左右轴承。该联轴器从动轴直接与轴系相连,建立联轴器与轴系结构模型,如图6所示。

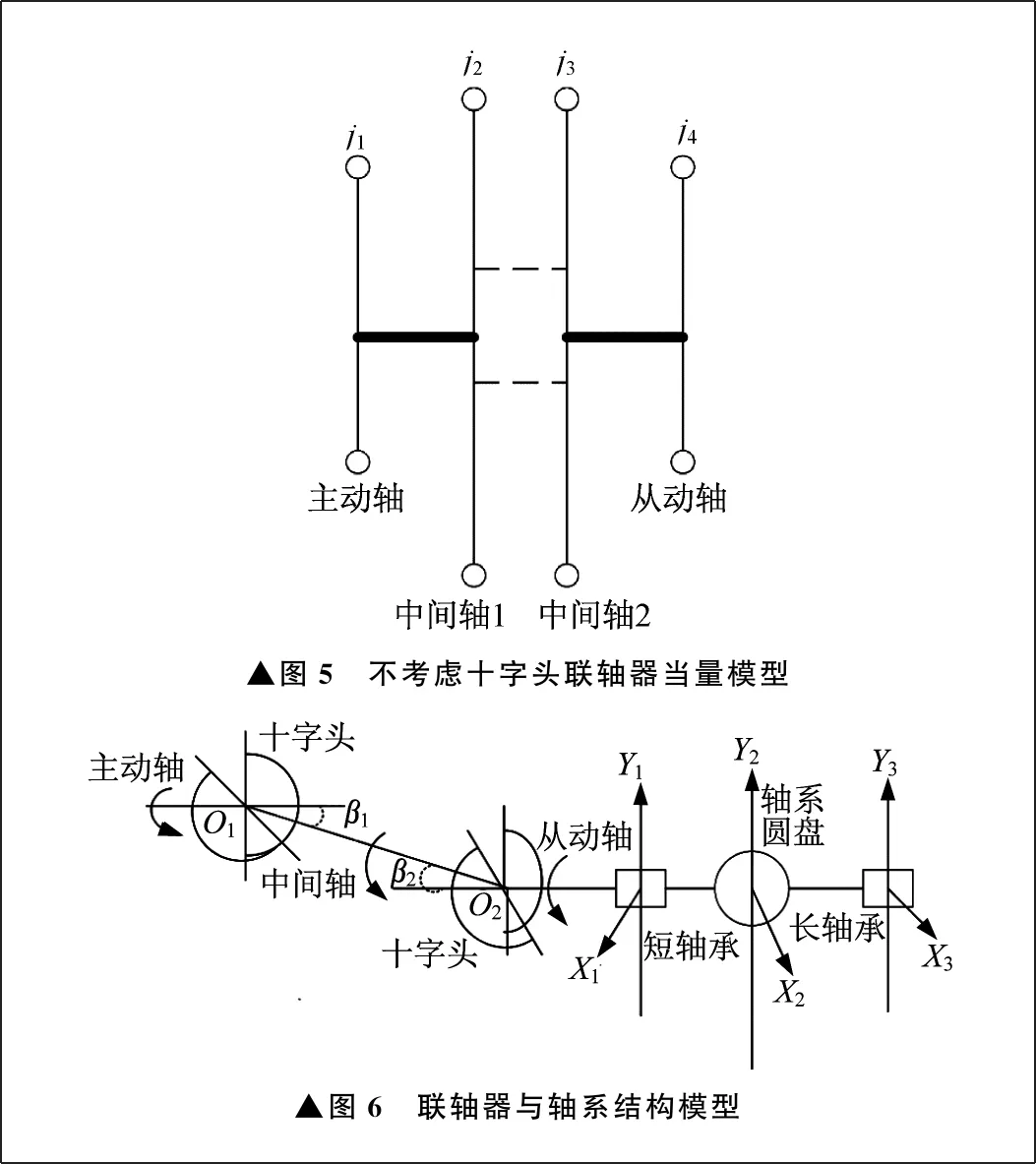
▲图5 不考虑十字头联轴器当量模型▲图6 联轴器与轴系结构模型

根据结构模型和简化模型,可以列出弯扭耦合微分方程:

(11)

(12)

(13)

(14)

(15)

(16)

(17)

=m6rω2cos(ωt)

(18)

=m6rω2sin(ωt)-m6g

(19)

(20)

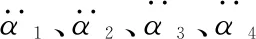
笔者通过对比β1=β2=1°、β1=β2=5°、β1=β2=8°来研究轴系振动,以短轴承处的计算结果进行分析。设置系统的初始参数如下:m5=40 kg,m6=100 kg,m7=80 kg,m8=200 kg,c1=5 000 N·s/m,c2=2 000 N·s/m,k=5×106N/m,λ1=λ2=0.1,r=0.06 mm。在MATALB软件中建立函数,不同β1、β2下短轴承处振动位移时域图、相图分别如图7、图8所示。

由图7可以发现,0～4 s内曲线起伏有较大的时间间隔,说明改变轴线夹角对轴系产生的振动较为迟钝。在0～4 s内,β1=β2=5°对应的曲线振动位移最大,β1=β2=8°对应的曲线振动位移最小,说明在初始时间内轴线夹角增大,导致轴系振动位移先增大后减小,与联轴器自身扭振有相似的规律。随着时间延长,振动位移曲线周期增多,最大幅值也随之增大,三种轴线夹角下的振动位移曲线没有绝对的最大值及最小值,但是峰值有明显区别,说明在变化范围内,长时间改变联轴器轴线夹角,对轴系产生振动的影响会越来越明显。

由图8对比不同轴线夹角下短轴承处振动位移相图,可以发现β1=β2=1°时,轨迹从原点开始运动,最终回到原点附近,近似形成两个圆环,轨迹较为有序且有周期性,中心基本没有偏离。β1=β2=5°时,轨迹从原点顺时针方向出发,形成两个周期,随着振动位移的增大,轨迹逐渐向左偏离。β1=β2=8°时,轨迹从原点顺时针方向出发,产生三个周期,随着振动位移的增大,轨迹先向左偏离、再逐渐向右偏移。在轴线夹角较小的情况下,形成的轨迹尽管不够光滑,但整体呈现为近似封闭圆环,且以中心为原点,可认为对系统的破坏性较小。增大轴线夹角,轨迹中心左移或者右移,但轨迹更加封闭圆滑,说明增大轴线夹角会对轴系振动产生一定影响,这一影响随时间延长而加重,与图7变化相对应。

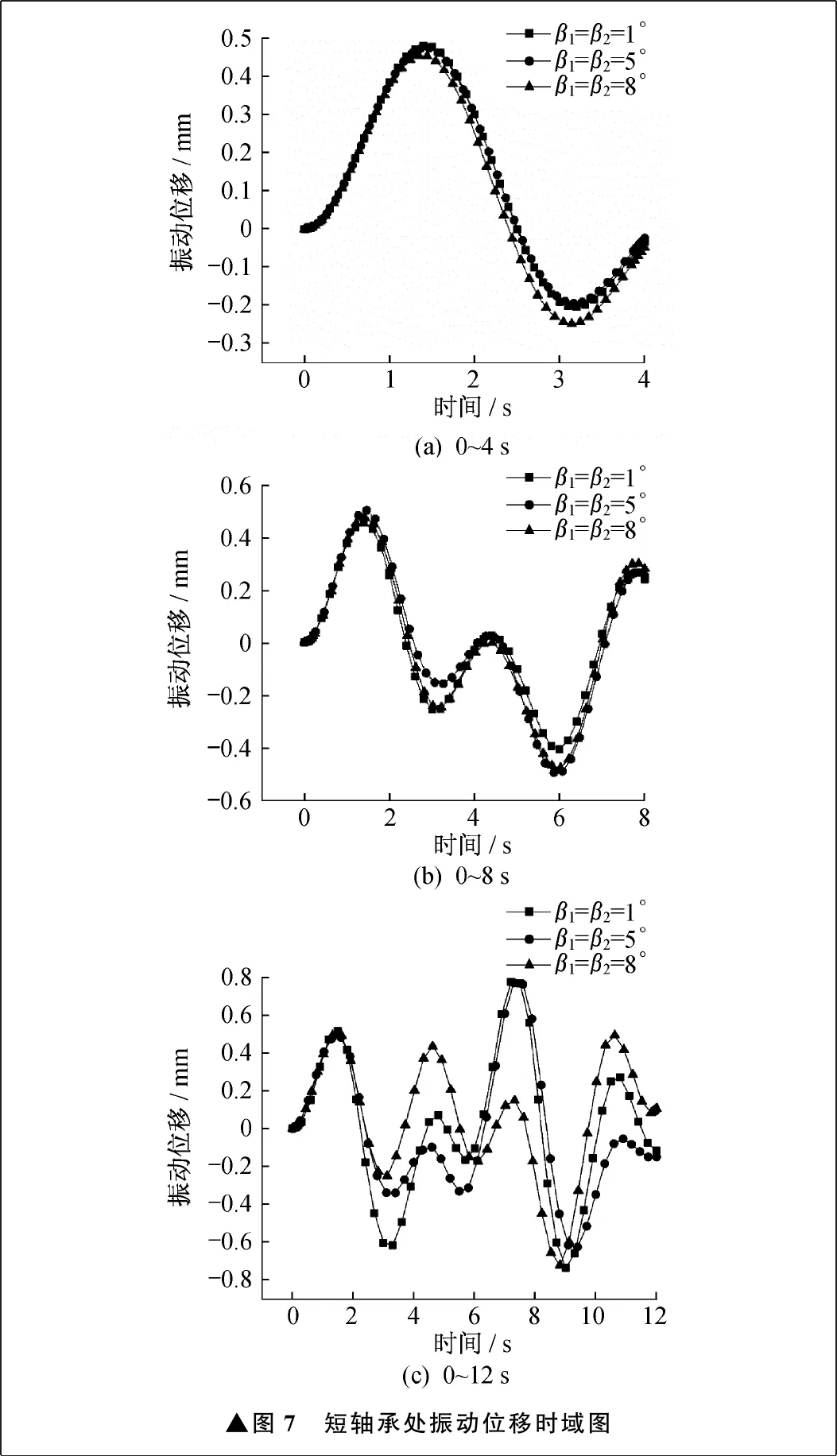
▲图7 短轴承处振动位移时域图

5 结束语

为研究双十字万向联轴器对船舶轴系振动的影响,笔者研究了双十字万向联轴器的扭转振动,并建立联轴器与轴系结构模型,进行数值仿真。

联轴器自由振动时,增大两轴线夹角,从动轴转角先增大后减小,可以认为轴线夹角变化对联轴器自由振动会产生一定影响,但不会破坏系统的稳定性。

轴系施加在联轴器上的横向力会对轴线夹角产生不可忽略的影响,初始夹角越大,对横向力的影响越大。为了减小横向力的影响,应避免较大的初始夹角。

在轴线夹角变化范围内,短时间改变轴线夹角,对轴系振动产生的影响不大。长时间改变轴线夹角,会使轴系产生一定的振动位移。由此可见,轴线夹角的改变应在合理的时间范围内。

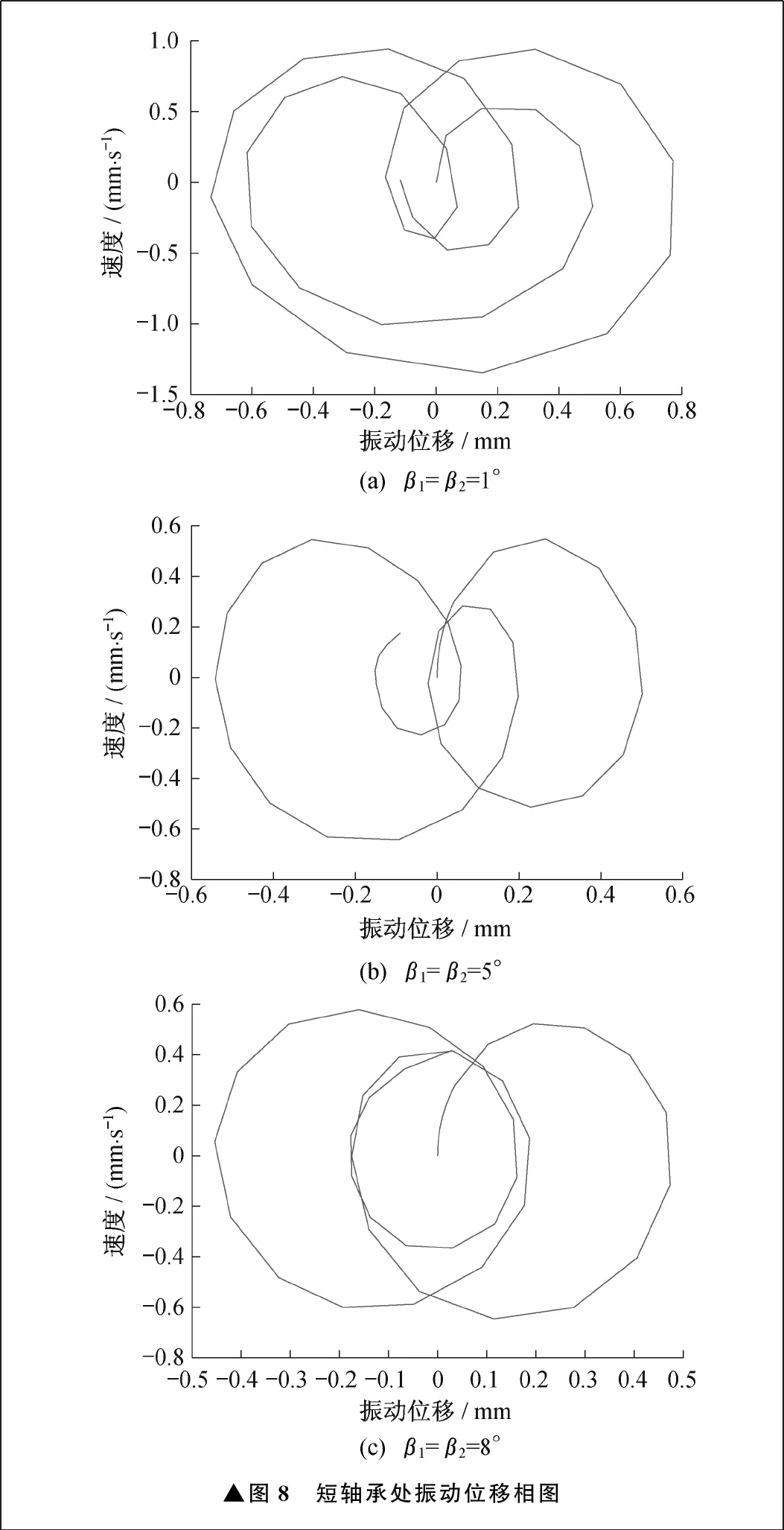
▲图8 短轴承处振动位移相图