基于SEM图像的阈值回归法计算印刷纸张孔隙率

薛美贵 陈红倩 李 慧 魏 华 李 伟

（1.东莞职业技术学院媒体传播系，广东东莞，523808；2.北京工商大学计算机与信息工程学院，北京，100048；3.北京工商大学计算机与信息工程学院，食品安全大数据技术

北京市重点实验室，北京，100048；4.北京联合大学管理学院，北京，100101）

纸张的孔隙率是指纸张中未被填充的空间体积与纸张总体积的比值。孔隙率是影响纸张微观结构的一个重要参数，直接影响其力学性能与物理、化学性能，如结构强度和对水、油墨、乳浊液、悬浊液等的吸收和过滤性能等，进而影响其在印刷、包装等相关领域的使用[1-2]。

目前常用的获知材料孔隙率的方法分为传统物理测量法与计算机图像处理法。传统物理测量法有压汞法、金相法、饱和介质法等，但这些测量方法存在实验时间长、实验条件苛刻、成本高等问题，且存在测量操作误差；计算机图像处理法一般是通过对材料使用扫描电子显微镜（SEM）或CT 扫描仪拍摄SEM 图像或CT 图像，运用图像处理技术将图像中的实体部分与孔隙部分识别出来并用于计算孔隙率。相比传统物理测量法，计算机图像处理法分析材料的孔隙率，可以减少大量的物理实验操作，能有效提高孔隙率检测的工作效率，降低实验造成的操作误差，并减轻实验造成的环境污染。

目前已有人将计算机图像处理法应用于多种X射线断层成像图像分割[3]、土石混合体材料[4]、网格圈织物[5]、土体结构的颗粒分布[6]、反应性粉末混凝土[7]、纳米材料孔径分布[8]、探井的地震阻抗体积[9]、储层岩石孔隙率等[10]的计算与分析，计算效果良好。

对于纸张SEM 图像的孔隙率计算目前主要有二维和三维[11]2 种方法。其中，二维方法中一个重要的步骤是二值化，即将纸张表面的SEM 灰度图像转换为黑白二值化图像，从而分析计算得到纸张表面的孔隙孔径分布、个数频率以及孔隙率。而二值化过程中，阈值的选取需要使用者具有一定的图像软件处理知识，每张图片孔隙与纤维分割阈值（即像素或是图片颜色亮度等）的设定受主观因素影响较大，具有不确定性，计算结果波动也较大[12]。另一方面，由于纸张纤维材料的类型多样，不同类型纤维的表面处理工艺差异大，造成该方法在应用过程中出现计算结果误差较大的现象。所以，在二值化过程中选择合适的阈值是非常关键的，阈值的不同会导致二值化后识别的孔隙数目与大小不同，从而影响结果的可靠性[13]。

针对上述问题，本研究提出了一种基于阈值回归的纸张纤维材料SEM 图像孔隙率分析方法，整个分析方法分为两个过程:回归模型建立过程和回归模型应用过程。在回归模型建立过程中，将小部分样品同时进行物理实验和计算机图像处理，然后将物理实验结果和计算机图像处理结果组成联合数据集，依托联合数据集建立阈值回归模型。在回归模型应用过程中，使用建立的模型确定图像的最佳分割阈值，并用于计算机图像处理过程，从而降低孔隙率的计算误差。实验结果表明，本研究提出的方法能够有效降低计算机图像处理法的结果误差，并提高了计算机图像处理法在多种类型材料上的适应能力。

1 阈值回归模型建立

在阈值回归模型建立过程中，选取少量纸张样品，通过同时进行计算机图像处理和物理实验，获取信息建立模型，阈值回归模型建立过程如图1所示。

图2为一幅典型的非涂布纸SEM 图，其为高分辨率的类灰度图片，图像格式为.tif。图2 中显示了纸张的内部纤维结构，易于研究者们进行观察、分辨纤维和孔隙结构。以图2为例，模型建立过程具体描述如下。

1.1 图像初步处理

针对SEM图像的初步处理过程，包括以下几步。

（1）对纸张SEM 图像进行滤波平滑处理，以降低拍摄过程中产生的噪声。在本研究实验中发现，通过“中值滤波法”能够有效去除图像中的高斯噪声和椒盐噪声等，平滑效果较好。

（2）对平滑后的图像进行灰度化处理，即将像素的颜色值转换为灰度值，灰度化处理后的图像如图3所示。

1.2 获取图像灰度信息

纸张SEM 图像转换为灰度图像后，将获取图像的以下3方面灰度信息。

（1）图像的全局灰度信息，以此确定图像拍摄时亮度、对比度的影响，为便于描述，命名第i 幅图像的全局灰度值为Ai。

图2 非涂布纸SEM图（×200）

图3 纸张SEM图像平滑和灰度化处理后的结果图（×200）

（2）通过点选图像的多处纤维位置，确定图像中纤维处的平均灰度值，所点选的纤维位置个数可以根据需要自行设定，本研究实验表明一般设定为5个较为稳定，为便于描述，命名第i 幅图像的纤维平均灰度值为Bi。

（3）通过点选图像的多处孔隙位置，确定图像中孔隙处的平均灰度值，所点选的孔隙位置个数可以根据需要自行设定，本研究实验表明一般设定为5个较为稳定，为便于描述，命名第i 幅图像的孔隙平均灰度值为Ci。

1.3 获取图像最佳分割阈值

对纸张样品进行物理实验，获取纸张的物理实验孔隙率，物理实验获取的孔隙率结果一般来说准确度高，且实验误差小，可以认为是纸张的真实孔隙率，为便于描述，命名第i 幅图像对应的物理实验孔隙率值为Pi。针对图像平滑和灰度化处理后的图像，根据图像对应材料的真实孔隙率，获取其最佳分割阈值。

在图像分割处理中低于分割阈值的像素点划分为孔隙，高于分割阈值的像素点划分为纤维，统计孔隙像素在整个图像中的占比即为孔隙率。最佳分割阈值是指当分割阈值为Di时，通过对灰度图像进行处理计算出的孔隙率值最接近于物理实验孔隙率值Pi。

1.4 回归模型参数计算

通过图像处理过程，可获得全局灰度值、纤维平均灰度值和孔隙平均灰度值，将每个纸张样品SEM图像的这3个变量作为模型的自变量，将每个图像对应的物理实验孔隙率对应的最佳分割阈值作为模型的因变量，建立起自变量与因变量之间的关系模型，该模型的目的是预测样品图像中能够分割孔隙和纤维的最佳分割阈值。本研究选取的是多元线性回归模型，该模型能够很好地拟合孔隙、纤维处以及全体图像的平均像素与最佳分割阈值之间的关系，通过前3个变量实现对最佳分割阈值的预测。该模型如式（1）所示。该模型中的参数可以通过Python、R 语言等的算法进行求解。

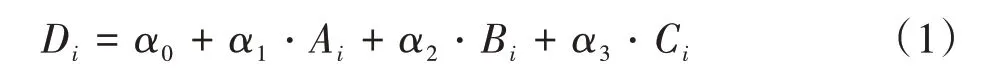
式中，Di为第i 张图像的最佳分割阈值；Ai、Bi、Ci分别为图像全局灰度值、图像纤维处以及孔隙处平均灰度值。

将数据分割为训练集和测试集，通过训练集获取回归模型参数。需要注意的是，回归模型参数的计算，需要多组数据才能进行计算，数据量越大一般来说所获取的模型越准确。模型训练完后，通过测试集获取回归模型误差，假如误差范围符合要求，则模型建立完成。

2 阈值回归模型应用

在阈值回归模型应用过程中，将需要确定孔隙率的样品，拍摄SEM 图像后进行平滑处理和灰度化处理；然后依次获取其全局灰度值、纤维平均灰度值、孔隙平均灰度值；然后将这3个值作为自变量分别代入式（1），即可计算出最佳分割阈值，并统计孔隙像素占比，从而获得纸张孔隙率。

实验结果表明，本研究方法建立的阈值回归模型，在获取最佳分割阈值时具备较好的分割性能，且对孔隙率的计算误差也较小。图4是通过本研究模型获取的最佳分割阈值获得的1 个图像分割结果实例（二值化图像已反转）。

3 结果与讨论

3.1 应用系统及使用过程

本研究已经实现了阈值回归模型的建立和应用系统，系统能对纸张样品图像进行处理，获得图像的全局灰度值、纤维平均灰度值、孔隙平均灰度值，在模型建立阶段，通过输入图像对应的物理实验孔隙率，即可进行模型训练。图5是本研究应用系统建立模型的具体流程。

图4 阈值回归模型的图像分割结果（反转）（×200）

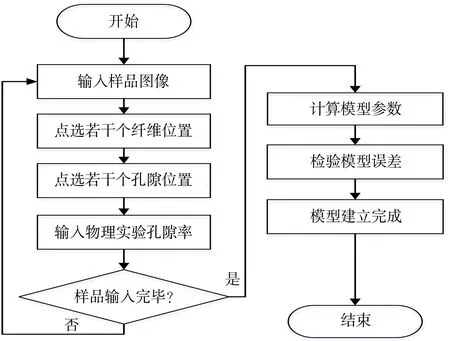
图5 应用系统建立模型的流程图

模型建立完毕后，使用过程中可根据单个纸张样品的图像计算其孔隙率，使用方法为:输入纸张样品图像，点选若干纤维位置及孔隙位置，即可计算获得其孔隙率。具体应用过程与结果展示如图6所示。

3.2 实验数据及分析

本研究针对一组纸张样品进行基于阈值回归模型的孔隙率模型建立和应用过程，其中纸张样品的灰度图像处理结果如表1所示。

对纸张样品进行物理实验，获得其物理实验孔隙率值，通过对纸张样品的灰度图像调整分割阈值，获得最接近于物理实验孔隙率值的最佳分割阈值及分割阈值为Di时与物理实验结果的误差，结果见表2。

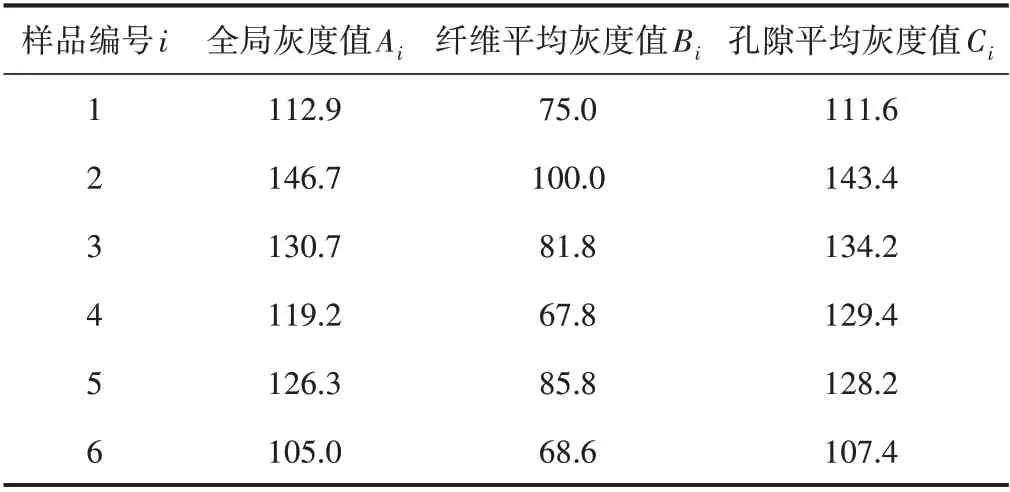
表1 纸张样品灰度图像处理结果（部分）

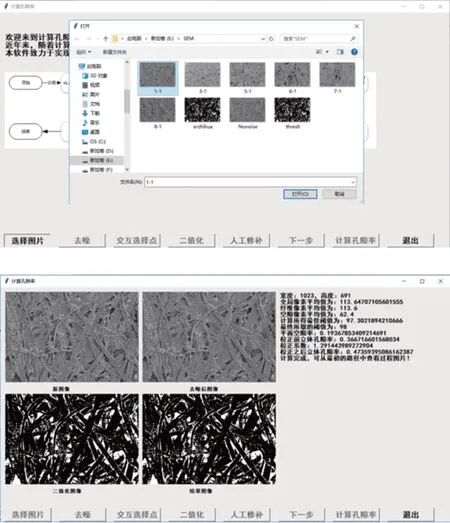
图6 应用模型计算的过程与最终结果展示

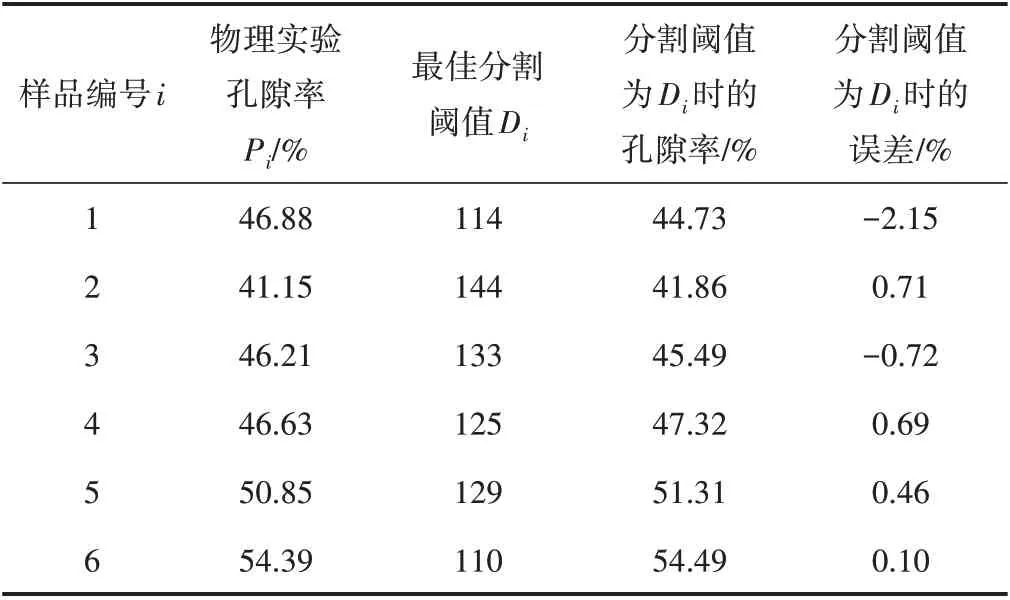
表2 样品的物理实验孔隙率、物理实验结果对应的最佳分割阈值及校验误差（部分）

通过R语言的运行环境获得各自变量的系数如表3所示。

根据表3中系数建立的回归方程如式（2）所示。

式中，Di为第i 张图像的最佳分割阈值；Ai、Bi、Ci分别为图像全局灰度值、图像纤维处以及孔隙处平均灰度值。

表3 阈值回归模型的各变量系数

表4 和表5 分别为本研究模型中所给出的纸张样品的图像处理结果和孔隙率计算结果，从表中可以看出，本研究提出的模型应用于样品的孔隙率计算误差率较小。

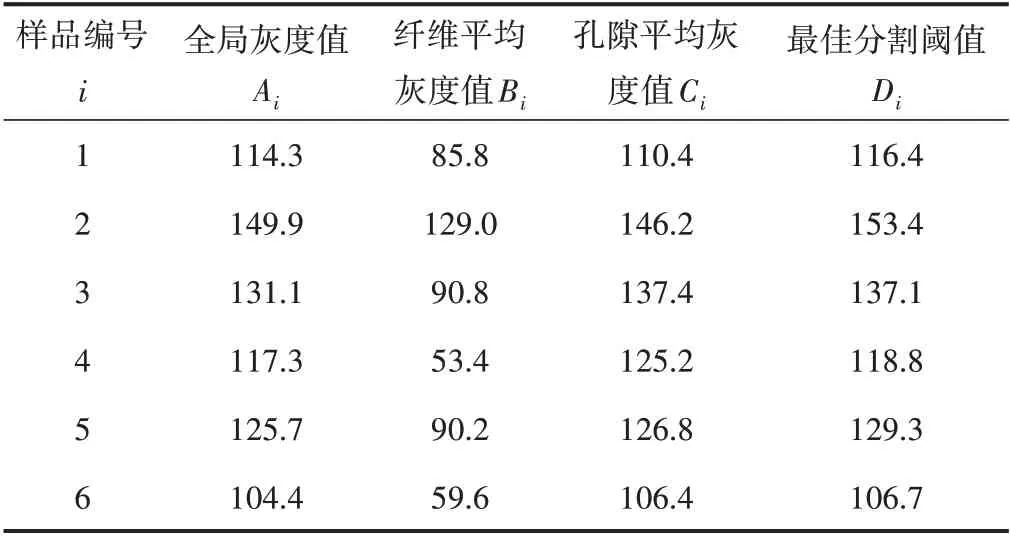
表4 模型应用的纸张样品图像处理结果（部分）

表5 模型应用的纸张样品孔隙率计算结果 %

4 结 论

针对非涂布纸张孔隙率的计算机图像处理法中，分割阈值确定受主观因素影响大的问题，本研究提出了一种使用阈值回归模型降低处理误差的方法。本方法通过针对小部分纸张样品，同步进行物理实验和图像处理，使用两部分实验数据对阈值模型进行训练，从而获取最佳分割阈值。实验结果表明，本研究提出的方法，应用于纸张孔隙率计算时，能够将图像处理过程的最佳分割阈值选取过程客观化，从而有效降低图像处理过程的结果误差，并使其在多种类型纸张上均具备较高的适应能力。