吉林省饮马河洪水演进数值模拟研究
李 航,丁 曼,徐贵新
(吉林省水利水电勘测设计研究院,长春 130021)
饮马河是吉林省第二松花江左岸最大支流,发源于四平市伊通县地局子乡老爷岭东南,流经伊通县、磐石市、永吉市、双阳区、九台区、德惠市、农安县和长春市二道区等8个市县(区),于农安县靠山镇红石垒屯汇入第二松花江,集水面积18 247 km2,其中石头口门水库以上集水面积4 944 km2。饮马河河道长度387.5 km,流域平均高程300 m左右。伊通河流域其上游属丘陵岗地,下游地形波状起伏,两岸河谷较开阔,地势较高部分大都开垦为旱田,河谷平地大部分开垦为水田。流域水系发育、支流较多,较大支流依次有伊通河、双阳河、雾开河、岔路河、三道沟河和小南河等[1]。
分析范围为饮马河石头口门水库至饮马河河口,包括沿岸的防洪保护区。其中,一维河道模型的构建范围为石头口门水库到饮马河河口,范围内的主干河道长度为110 km;二维水流模型的构建范围为饮马河沿岸的防洪保护区。

图1 饮马河(石头口门水库以下)水系示意图
1 洪水分析方法及模型构建
1.1 洪水分析方法
饮马河石头口门水库放流与区间小南河、雾开河与伊通河等支流组成编制区域的洪水来源,干流来水控制站为石头口门水库站和德惠站,支流来水控制站为九台站、农安站等。
采用MIKE ZERO系列洪水模拟水动力软件进行洪水分析,包含河道洪水演进、溃堤洪水以及淹没区洪水演进,分别建立MIKE11一维非恒定流模型模拟饮马河河道洪水演进过程,DAMBRK方法计算堤防溃堤洪水,MIKE21二维非恒定流模型模拟饮马河防洪保护区的洪水演进过程[2]。由于二维水流模拟的上边界为堤防溃口处的流量过程,而溃口流量又取决于溃口上下游(河道与淹没区)的水位差,因此将上述3种模型相互耦合、联立求解,系统模拟溃堤后对防洪保护区的影响。
1.2 模型原理
1.2.1 一维水动力学模型原理
圣维南(Saint-Venant)方程组为MIKE11一维非恒定流模型中的河道洪水运动的基本方程:
动量方程:
式中:Q为断面流量,m3/s;A为过水断面面积,m2;q为源汇的单宽流量,m2/s;x为距离坐标,m;t为时间坐标,s;h为水位,m;C为谢才系数;R为水力半径,m;g为重力加速度,m/s2;α为动量校正系数。
1.2.2MIKE21二维水动力模型
二维非恒定流方程如下,为平面二维水流模型,由连续方程及动量方程组成:
式中:h为水深,m;Z为水位,m;u为X方向沿垂线平均的水平流速分量,m/s;v为Y方向沿垂线平均的水平流速分量,m/s;g为重力加速度,m/s2;n为糙率;q为源汇项,m/s。
1.3 模型构建
1.3.1 网格剖分
收集编制范围1∶10 000矢量地形图及数字高程,确定模型中防洪保护区分析范围,并设置开边界和闭边界,开边界为水流进出边界,闭边界为阻水边界。考虑无结构网格适应能力强并且灵活的特点,为提高边界处模拟精度,采用无结构三角形网格剖分[3],控制三角形网格最大面积不超过0.01 km2,且网格大小均匀,尽量剖分成等边三角形。见图2、图3。
图2 网格划分示意图
图3 局部网格划分示意图
1.3.2 计算时间和步长
河道断面间距、连接位置以及参数验证的水文站点位置等因素与一维河道模型空间步长设定息息相关,饮马河断面间距最小为50 m,作为MIKE模型中水位计算点间距,为了保证模型稳定准确运行,此次时间步长设定为30 s。
1.3.3 边界条件设置
根据编制范围河网分布,上边界位于石头口门坝址,根据石头口门水库调度规则,调节天然入库洪水过程线得到水库泄流过程,下边界位于饮马河河口,根据河口处实测断面分析计算得到水位-流量关系。区间小南河、雾开河与伊通河等支流作为点源以洪水过程线形式加载。
1.3.4 模型参数选取与验证
根据饮马河各断面河道河床的实际组成情况,并通过石头口门站、德惠站洪痕调查以及H-Q关系曲线反推糙率验证而得到的糙率成果,主槽值选用0.03,边滩选用0.05。
将防洪保护区按照土地利用图分为6种地表类型,各类下垫面糙率参考《洪水风险图编制导则》有关数值,并根据典型区域实测大洪水淹没资料进行分析率定。见表1。

表1 饮马河防洪保护区糙率表
1.3.5 模型验证
以饮马河石头口门水库2010年7月21日实测泄流为上边界,结合水文年鉴中洪水要素摘要实测流量,模拟大汛期洪水,进行模型参数验证。通过调整饮马河各断面的河床主槽及边滩的糙率参数,使干流区间内的德惠水文站处经模型模拟得到的流量和水位与实测值接近吻合。当洪峰流量Qm和水位H的误差分别控制在10%和20 cm以内[4],说明河道参数取值较为合理。见图4。
利用已经参数验证后的一维河道模型,采用饮马河干流及各支流50年一遇设计洪水(以1953年作为典型年,干流洪峰流量Qm为700 m3/s)作为边界条件,分析计算饮马河石头口门水库坝下至河口段河道水面线,并与已通过上级水利主管部门审查的50年一遇设计水面线成果进行对比(图5),模拟水面线成果与堤防设计成果平均误差为10 cm,最大误差为21.4 cm,验证结果符合要求。
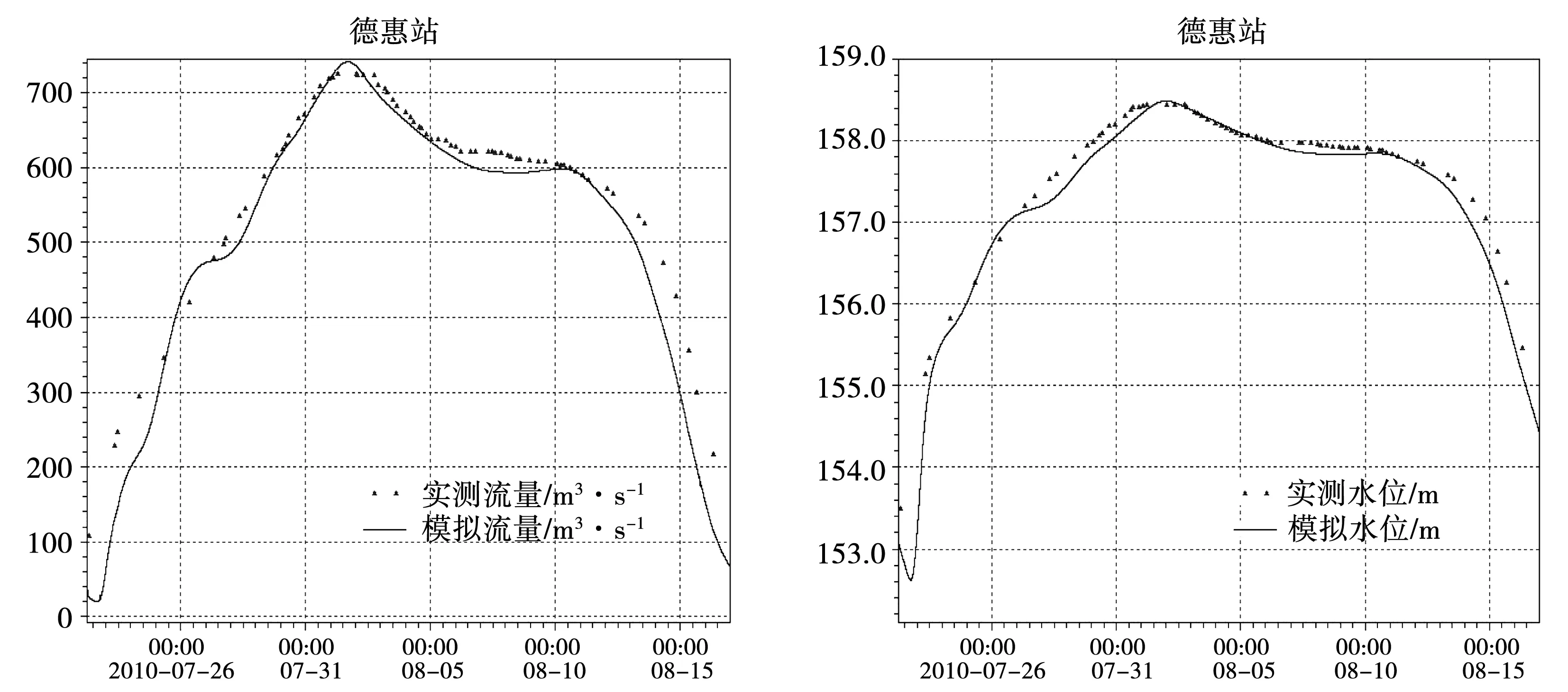
图4 德惠站模拟值与实测值对比图(左图为流量,右图为水位)
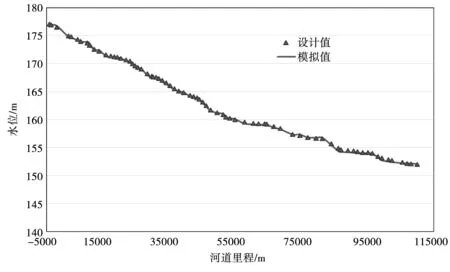
图5 模拟与设计水面线对比图(P=2%)
2 洪水分析成果
2.1洪水分析计算
以陈家崴子溃口20年一遇洪水方案为例,饮马河干流按20年一遇洪水控制,各支流相应洪水组合,洪水过程2015年8月2日0时至9月20日6时。8月28日8时,德惠市农村段陈家崴子险工处河道达到特征水位,堤防开始发生溃决,最大溃口宽度50 m,溃口最大流量Qm=297 m3/s。8月24日12时,饮马河下游里程75 606 m处有小部分水漫出,其余堤防均未发生漫堤现象。至洪水过程结束,共进入饮马河防洪保护区总水量4 451×104m3,最大淹没范围61.22 km2,最大淹没水深达4.42 m,最大洪水流速达1.29 m/s。见图6、图7。
2.2 水量平衡分析
2.2.1 淹没区水量平衡分析
计算模型中的进水量、出流量以及防洪保护区内淹没的水量,并将入流量减去出流量后得到的差值,与防洪保护区内淹没的水量对比,若误差在1%以内,说明洪水模拟结果合理。经计算,陈家崴子溃口方案进水量11 209.78×104m3,出水量6 759.26×104m3,最终水量4 451.41×104m3,相对误差0.02%。
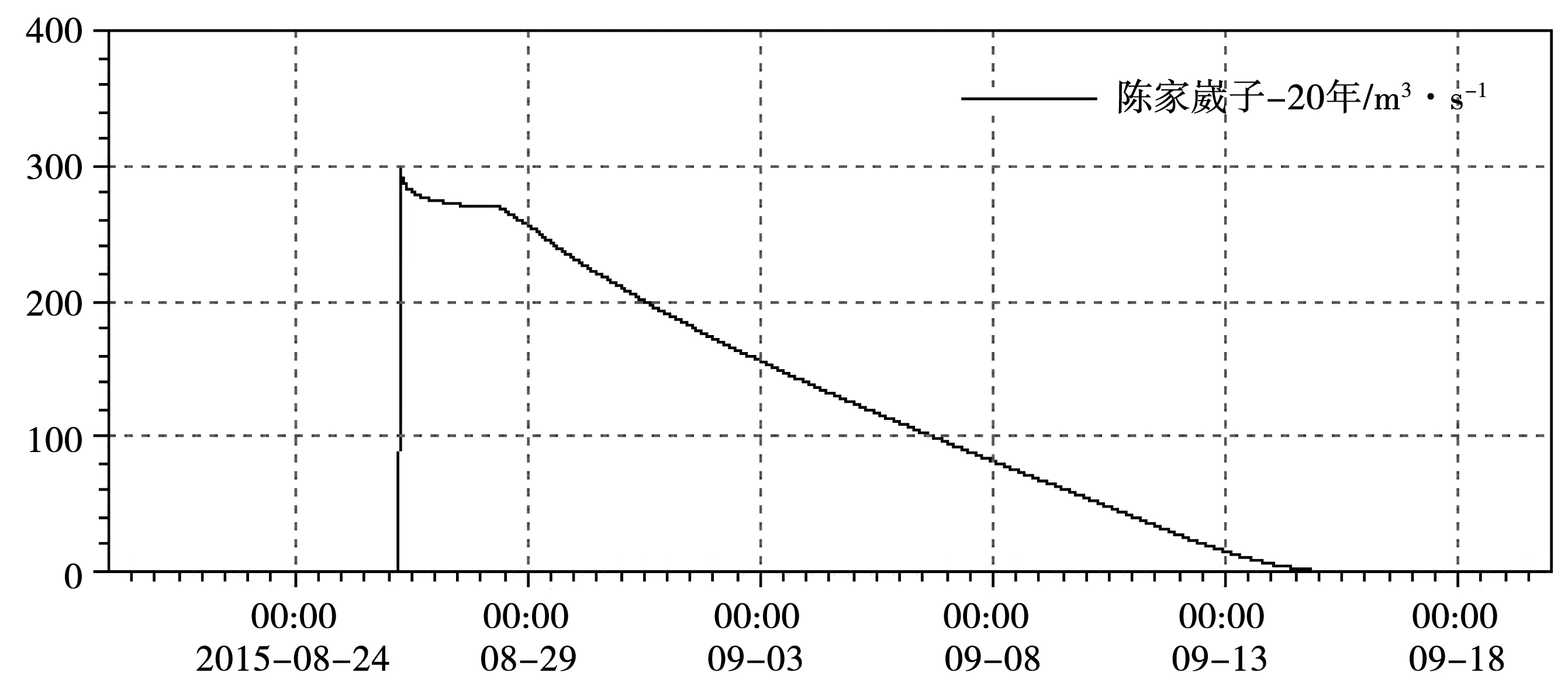
图6 饮马河陈家崴子溃口流量过程图
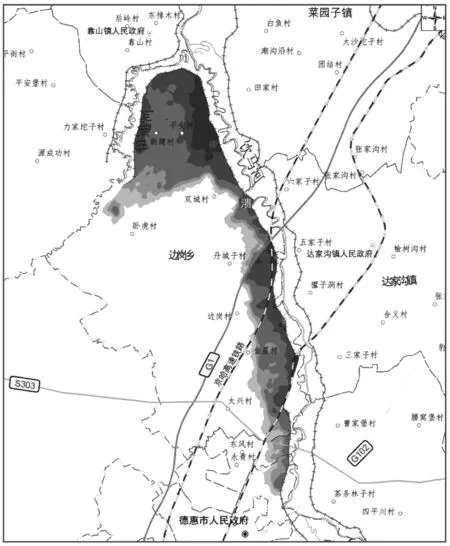
图7 饮马河陈家崴子溃口最大淹没水深示意图
2.2.2 耦合模型水量平衡分析
在一、二维耦合模型计算中,溃堤模型作为桥梁,将一维水动力模型水量传递给二维水动力模型。由于是三者耦合计算,如模型设置不合理,会造成水量缺失现象,影响结果的可信度。通过对比一维模型输入二维模型水量与二维模型接收一维模型水量情况检验计算合理性,陈家崴子溃口发生20年一遇洪水时,一维水动力模型河道出流水量11 209.78×104m3,二维水动力模型边界入流水量11 209.78×104m3,水量相差为0,说明模型计算合理[5]。
3 结 语
通过MIKE系列软件构建一、二维水动力模型,可以直观展示洪水在发生溃堤后产生的最大淹没范围、最大淹没水深及最大洪水流速等信息,同时也可展示洪水演进动态过程,能够提取洪水到达时间、洪水淹没历时等洪水风险要素。本文以饮马河陈家崴子溃口20年一遇洪水方案为例,介绍了MIKE11和MIKE21模型原理,模型构建中的网格剖分、设置边界条件、模型参数验证等,建立具有较高模拟精度的水动力耦合模型,模拟成果经水量平衡分析后合理可靠,成果可为后续的洪灾损失评估和防洪减灾提供技术支撑。

