碾压式沥青混凝土心墙坝三维静动力数值模拟研究
李燕波
(新疆水利水电勘测设计研究院,乌鲁木齐 830000)
碾压式沥青混凝土心墙坝具有结构简单、经济合理、易于施工等优点,该坝型在我国水利枢纽工程中得到广泛的应用[1]。受制于气候、地理条件等因素,近年来新疆新建50余座碾压式沥青混凝土心墙坝,如阿克肖水库、努尔水库等,工程建设数量及设计、施工技术均位居世界前列。目前关于碾压式沥青混凝土心墙坝的研究较多,但研究方向主要集中于筑坝土料、沥青混凝土等力学特性[2]、施工过程质量控制[3]以及运行管理、变形监测[4-5]等,关于坝体受力特性也主要为二维平面应力应变数值研究[6-7],无法真实反映坝体在三维空间状态下的受力特性。鉴于此,以新疆某水利枢纽工程为研究对象,采用非线性邓肯-张E-B模型进行大坝三维有限元静力计算,采用等效线性粘弹性模型进行大坝三维有限元动力计算,采用三维等价结点力法研究坝体地震永久变形,主要研究了坝体在静动力条件下坝体和防渗体的应力、变形以及基座与心墙的相对位移等受力特性,对类似工程的建设有十分重要的意义。
1 工程概况
该工程位于新疆某河山区中游河段上,是该河上的控制性工程,起着龙头水库的重要作用,主要承担防洪、灌溉和发电的工程任务。水库总库容为0.927×108m3,正常蓄水位为1 894.0 m,死水位1 873.0 m,电站总装机容量为26 MW,多年平均年发电量为0.777×108kW·h。工程由碾压式沥青混凝土心墙坝、溢洪道、泄洪冲沙洞、发电引水系统及电站厂房等组成,工程为Ⅲ等中型工程,大坝为2级建筑物,各泄水建筑物及发电引水建筑物、电站厂房为3级建筑物,次要建筑物为4级建筑物,临时建筑物为5级建筑物。地震设防烈度Ⅷ度。
2 筑坝材料试验及参数确定
2.1 筑坝材料试验
静三轴试验固结围压分别为500,1 000和1 500 kPa,研究材料的变形和强度特性,包括应力-应变关系、体变-应变关系,提供有限元静力计算的邓肯张E-B模型参数。动模量和阻尼比试验对坝壳料、过渡料、坝基料进行动力变形特性循环加载试验,固结围压分别为500,1 000和1 500 kPa,测定材料动应力和动应变的关系曲线,确定最大动剪切模量Gmax与有效固结压力的关系、动剪切模量G和阻尼比与动剪应变的关系,整理等效线性有限元动力计算的模型参数。永久变形试验对坝壳料、过渡料、坝基料进行固结排水循环加载试验,研究在不同围压(σ3=500,1 000和1 500 kPa)、不同固结比(Kc=1.5和2.0)和不同动剪应力比(σd/σ3=0.4和0.8)条件下,残余体积和剪切应变与振次的关系,为永久变形计算提供模型参数。试验设备选用500和1 500 kN的高精度大型液压伺服静动两用三轴仪,见图1。
固结排水剪试验方法参照《土工试验规程》(SL237-1999)的有关规定,试验按以下方式进行,试样饱和后,对试样施加等向固结应力,当固结排水量达到稳定后,认为土样已经固结;采用应变控制或应力控制进行常规或复杂应力路径排水剪试验,直至试样剪切破坏。

图1 高精度大型液压静、动三轴仪
动剪切模量与阻尼比试验待试样饱和后,对试样施加等向固结应力,当固结排水量达到稳定后,认为土样已经固结完成;根据设定固结比,进一步给试样施加轴向应力,进行非等向固结,当固结排水量达到稳定后,认为土样已经非等向固结完成;关闭排水阀,然后在非等向固结应力和不排水情况下,施加轴向振动应力;从较小的动应力开始,逐级增加动应力幅值,每一级动应力幅值连续振动6周,测得轴向动应力-轴向动应变的滞回关系;每一级动应力幅的循环荷载结束后,打开试样的排水阀,以消散试样中因振动引起的孔隙水压力。
永久变形试验待试样饱和后,对试样施加等向固结压力,当固结排水量达到稳定后,进一步给试样施加轴向应力,当固结排水量达到稳定和孔隙水压力完全消散后,可认为试样非等向固结已经完成;然后在非等向固结压力和排水情况下,对试样轴向施加某一动应力幅的循环荷载[8]。
2.2 材料参数确定
根据本工程材料静力试验结果,确定坝壳料、过渡料和坝基料的邓肯张E-B模型参数见表1。
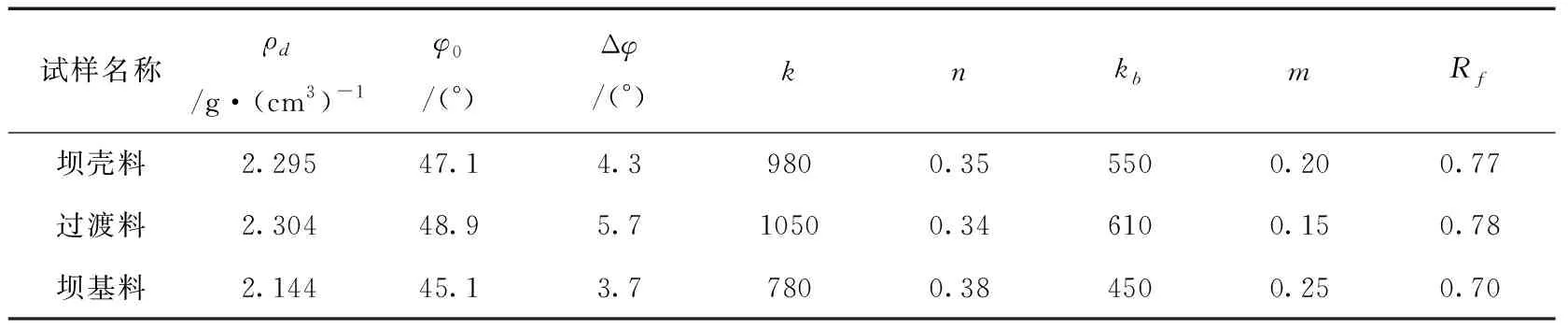
表1 静力试验邓肯张E-B模型参数
根据本工程材料动力试验结果,确定坝壳料、过渡料和坝基料的动模量与阻尼比试验结果见表2和表3。
根据本工程材料永久变形试验结果,确定坝壳料、过渡料和坝基料的双曲线永久变形模型参数见表4。
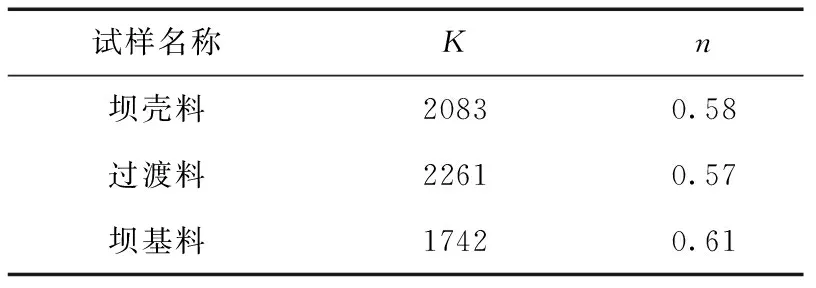
表2 动剪切模量系数和指数
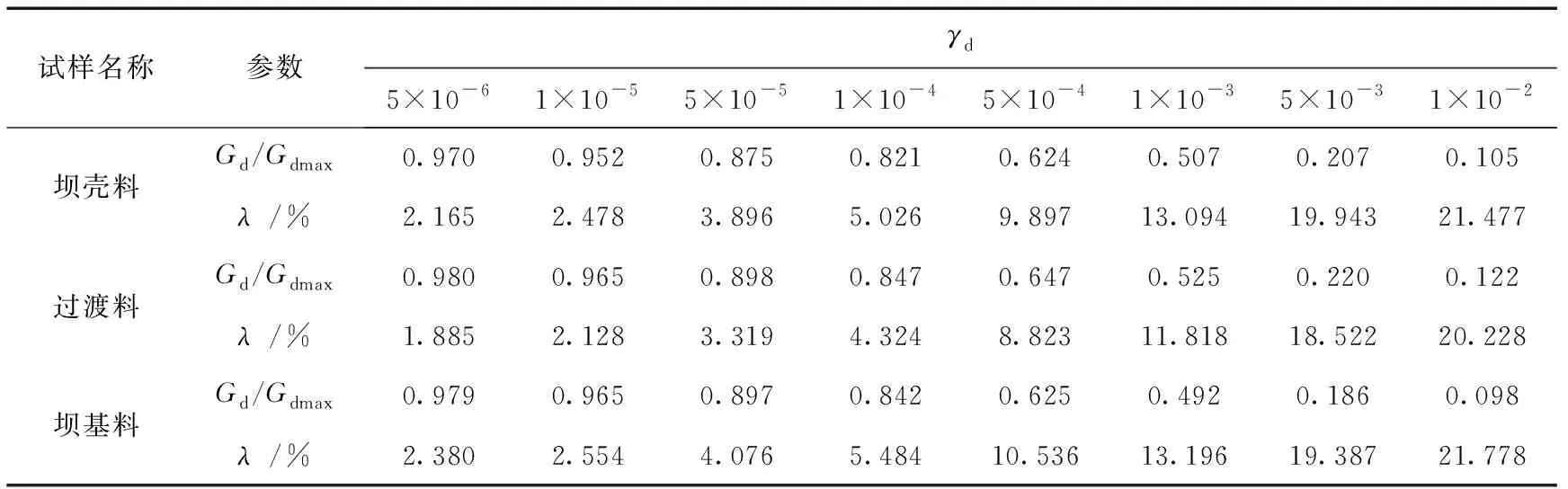
表3 归一化的动剪切模量Gd/Gdmax和等效阻尼比λ

表4 双曲线永久变形模型参数
3 分析模型及动力参数
碾压式沥青混凝土心墙坝典型断面见图2。有限元荷载步共分为48级,其中填筑分34级,蓄水分14级。大坝填筑完成之后开始蓄水,蓄至正常蓄水位1 894 m。沥青混凝土心墙坝填筑采用分层激活单元法模拟。蓄水时水下部分施加浮托力,同时水压力以面力的形式作用在沥青混凝土心墙和基座上。其中,竣工期为第34步,满蓄期为第48步。
坝体三维有限元网格见图3,沥青混凝土心墙有限元网格见图4。
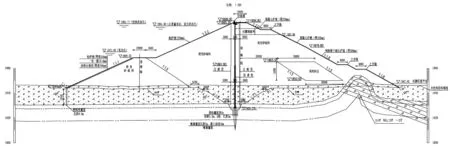
图2 大坝典型断面

图3 坝体三维有限元网格(单元158 364个;节点174 954个)

图4 心墙三维有限元网格(单元5 949个;节点11 944个)
三维有限元模型单元数为158 364个,节点数为174 954个,自由度超过50万。筑坝料和沥青混凝土心墙料采用邓肯张E-B模型,混凝土基座采用C30混凝土材料,ρ取值2.40 g/cm3,E取值30 GPa,υ取值0.20。心墙与过渡料、基座与心墙之间设置接触面单元,计算参数参考同类工程[9-10],见表5。

表5 接触面模型参数
动力有限元网格与静力一致,动力计算采用等效线性模型,永久变形计算采用大工双曲线模型。高土石坝-河谷山体系统为一个能量开放的系统,山体河谷与坝体之间存在着不同程度的相互作用,外行的散射能量会向无限地基辐射。这些因素会导致坝体边界处各点的反应幅值及相位存在差异,地震波动效应的影响更加显著。因此,本次有限元计算地震动输入采用粘弹性边界和等效荷载共同实现,考虑大坝和基岩的动力相互作用及辐射阻尼。
动力计算时在模型底部和侧边施加粘弹性边界,以模拟地基无限域辐射阻尼的作用。人工边界是通过在边界节点上施加切向和法向的阻尼器来实现的,其参数可分别按下式计算:
Ct=ρ·Vs·ΔAi
(1)
Cn=ρ·Vp·ΔAi
(2)
式中:ΔAi为模型外边界节点i的控制面积(亦称代表面积);ρ为节点i处边界材料的密度;Vs与Vp分别对应节点i处边界材料的剪切波速与纵波波速[11-13]。见图5-图7。
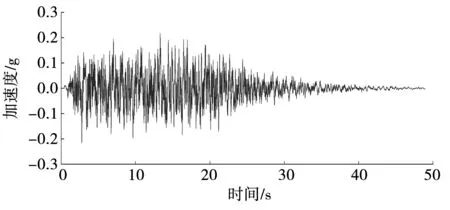
图5 顺河向地震加速度时程

图6 竖向地震加速度时程
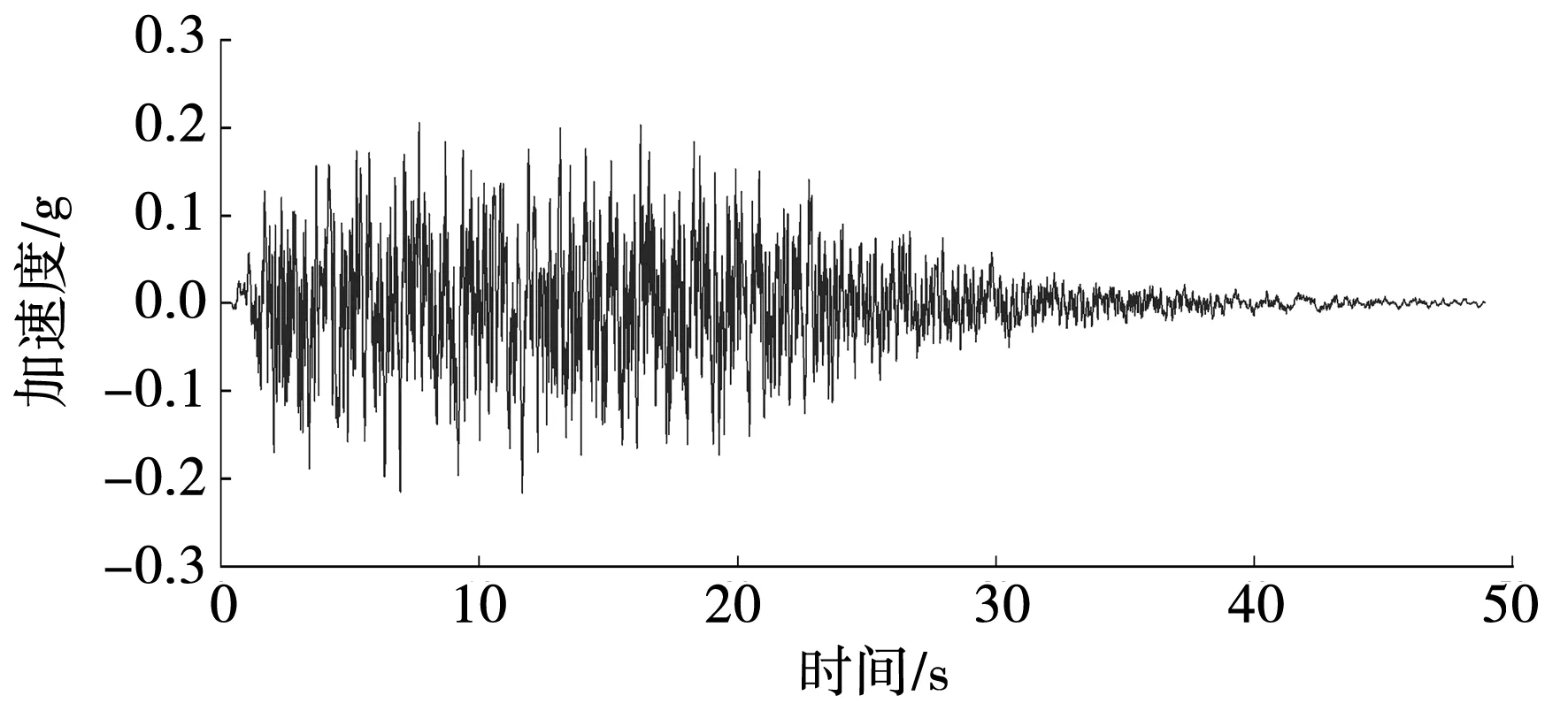
图7 坝轴向地震加速度时程
4 计算成果
4.1 静力坝体位移计算成果
通过大坝静力有限元计算,典型断面顺河向和竖向位移分布见图8-图11。

图8 大坝典型断面竣工期顺河向位移(cm,顺河向为正)
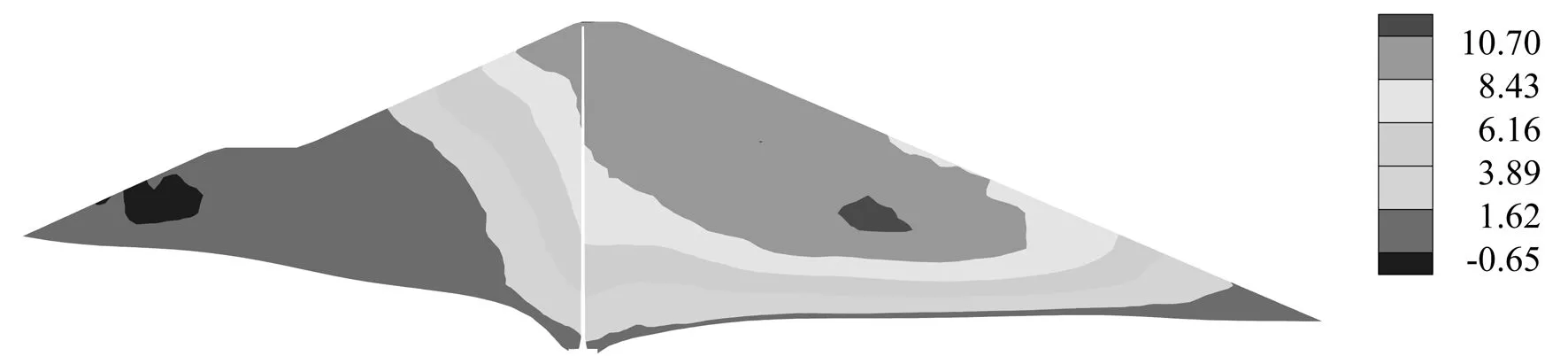
图9 大坝典型断面满蓄期顺河向位移(cm,顺河向为正)
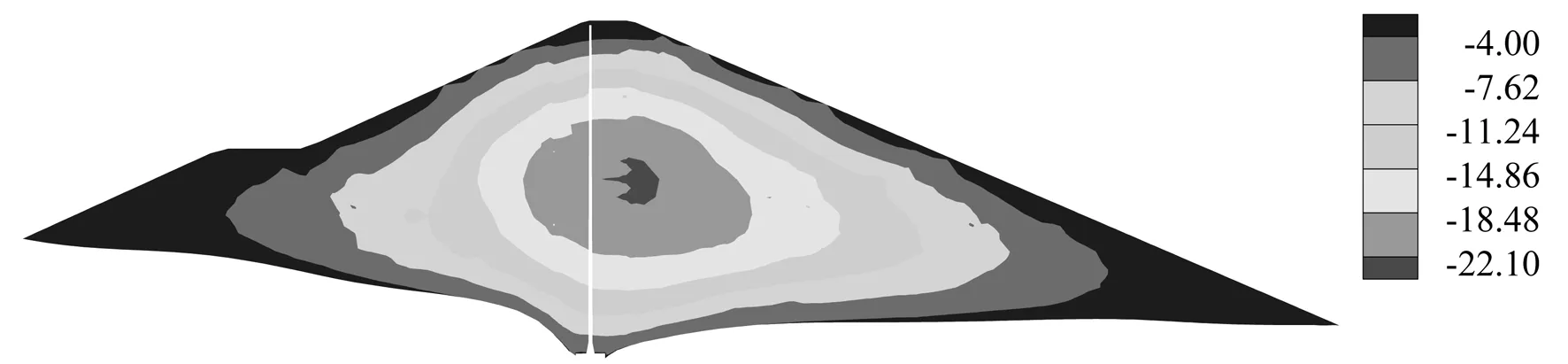
图10 大坝典型断面竣工期竖向位移(cm,沉降为负)
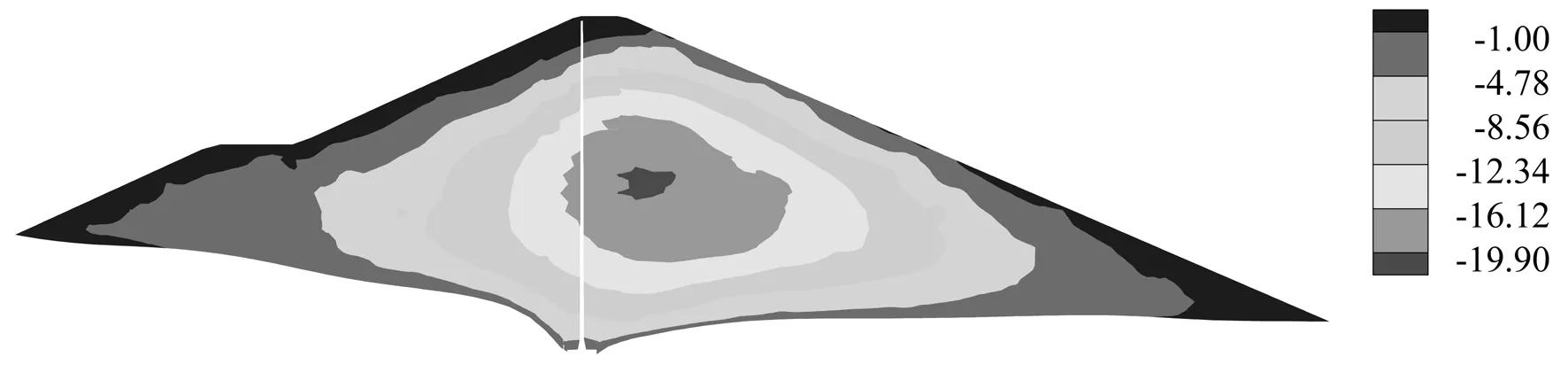
图11 大坝典型断面满蓄期竖向位移(cm,沉降为负)
分析可知,竣工期大坝沉降最大值为22.10 cm;满蓄期大坝沉降最大值为19.90 m。竣工期,顺河向位移最大值为1.85 cm(向上游)和6.80 cm(向下游);满蓄期,由于水压力作用,向上游变形区域和数值减小,向下游变形区域和数值增大,最大值为0.65 cm(向上游)和10.70 cm(向下游)。
4.2 静力坝体和坝基应力计算成果
通过大坝静力有限元计算,坝体和坝基应力分布见图12-图15。

图12 大坝典型断面竣工期大主应力(MPa,压为正)
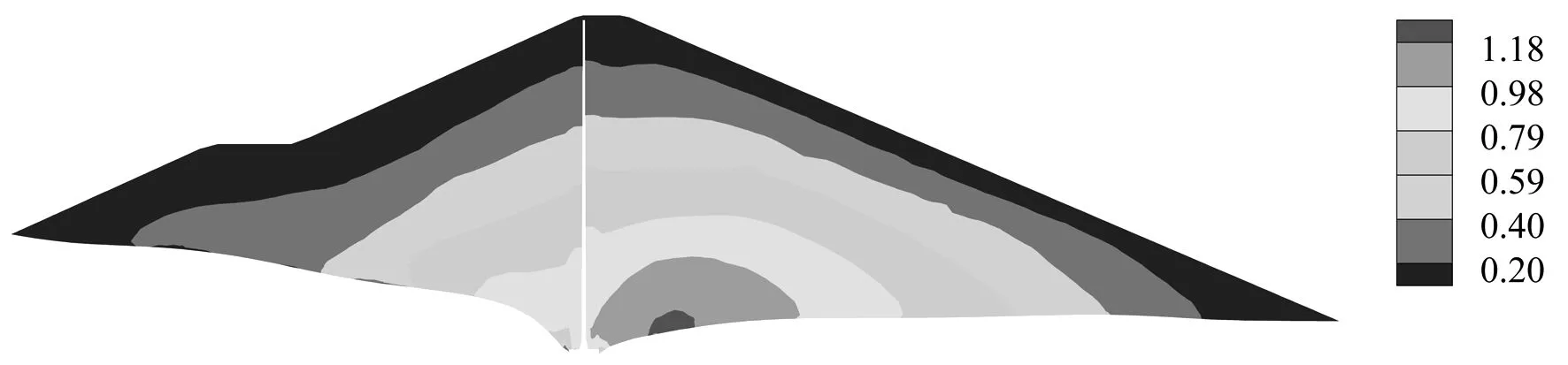
图13 大坝典型断面满蓄期大主应力(MPa,压为正)

图14 大坝典型断面竣工期小主应力(MPa,压为正)
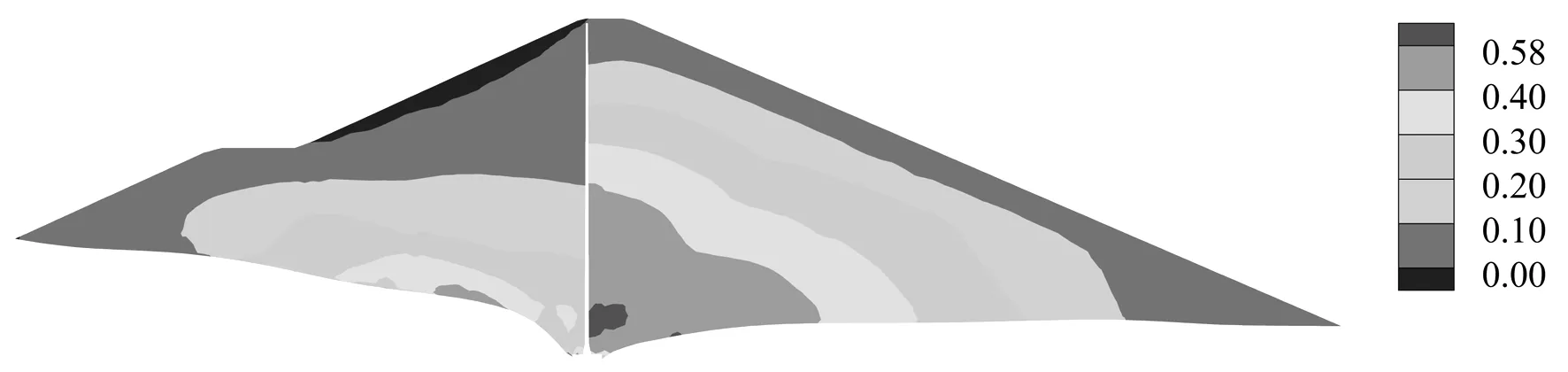
图15 大坝典型断面满蓄期小主应力(MPa,压为正)
分析可知,竣工期,坝体和坝基大主应力和小主应力最大值分别为1.22和0.59 MPa;满蓄期,由于浮托力的作用,主应力略有减小。
4.3 静力心墙应力计算成果
通过大坝静力有限元计算,沥青混凝土心墙的主应力分布见图16-图19。

图16 竣工期心墙大主应力(MPa,压为正)

图17 满蓄期心墙大主应力(MPa,压为正)

图18 竣工期心墙小主应力(MPa,压为正)

图19 满蓄期心墙小主应力(MPa,压为正)
分析可知,沥青混凝土心墙最大压应力为1.20 MPa(竣工期)和1.03 MPa(满蓄期),主要位于心墙底部。
4.4 静力水力劈裂计算成果
图20和图21分别为满蓄期心墙上游侧竖向应力、坝轴向应力与水压力差值分布。从图20-图21中可以看出,整个心墙大部分区域的竖向应力和坝轴向应力均大于水压力。相对于黏土心墙而言,沥青混凝土心墙发生水力劈裂的可能性较小,黏土心墙常用的水力劈裂评判标准(水压力小于竖向应力或坝轴向应力)用来评价沥青心墙也是偏于保守的。可以认为沥青混凝土心墙不会发生水力劈裂。
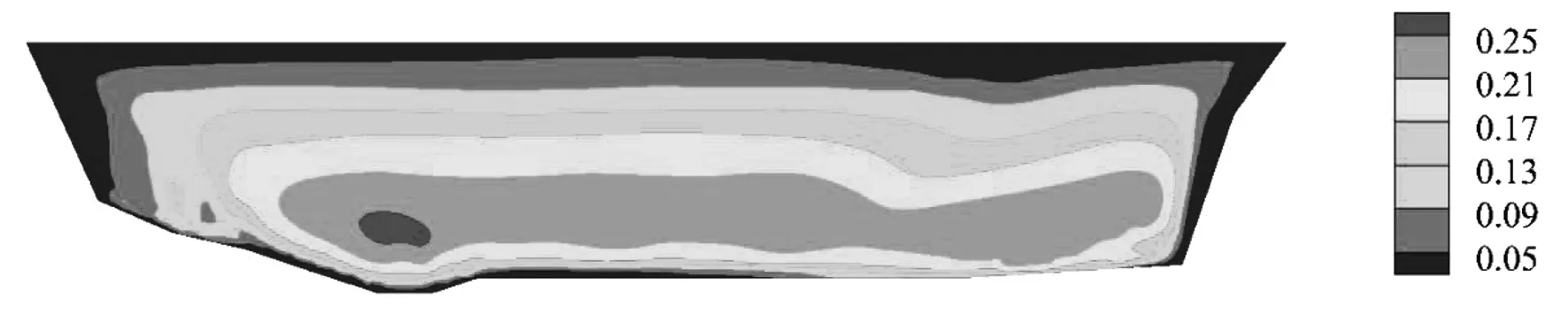
图20 满蓄期心墙竖向应力与水压力差值云图(MPa)
4.5 静力心墙-基座相对位移
竣工期心墙与岸坡基座沿顺河向最大错动位移为0.18 cm,位于靠近右岸顶部区域;满蓄期由于水压力推力作用,最大值增至0.65 cm,均位于坝体最大横断面附近。竣工期心墙与岸坡基座沿岸坡向最大错动位移为1.50 cm,满蓄期为1.30 cm,均位于右岸略高于1/2坝高的区域。
静力计算结果汇总详见表6。
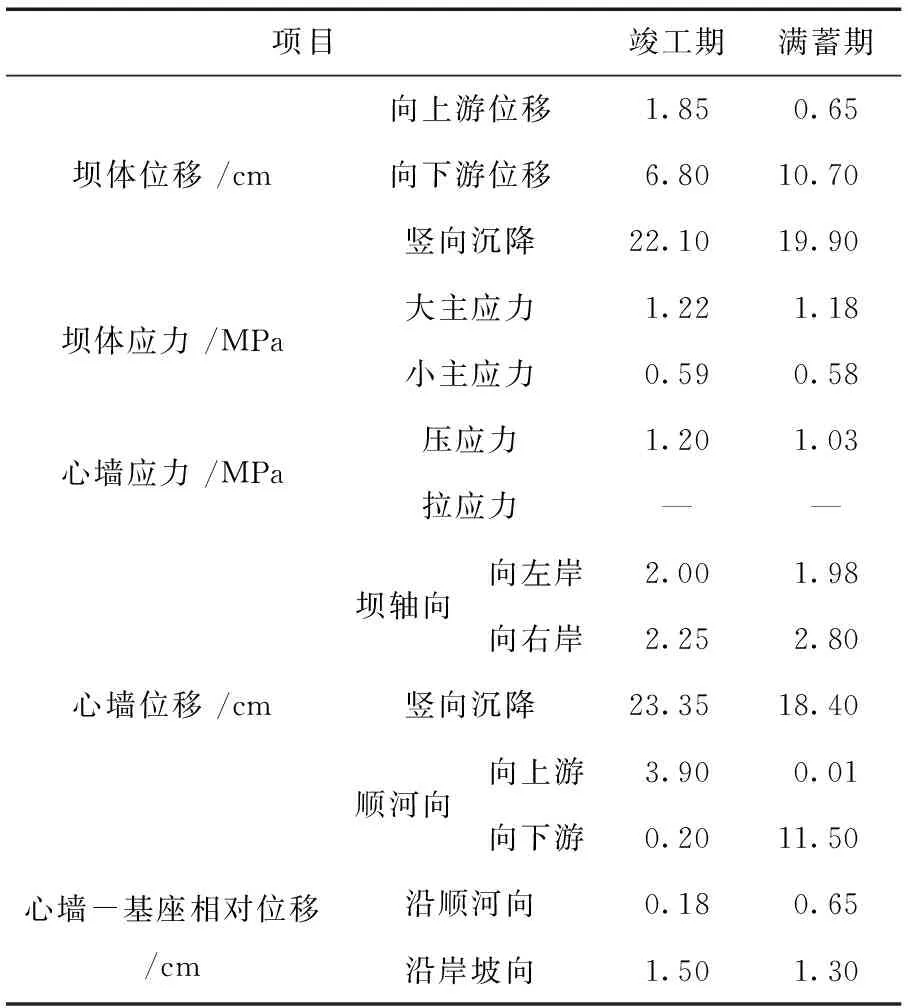
表6 大坝三维静力计算结果极值
4.6 坝体和坝基地震反应
大坝地震过程中最大动位移反应极值分布见图22-图24,坝体顺河向最大动位移为3.80 cm,竖向最大动位移为1.90 cm,坝轴向最大动位移为4.20 cm,最大值均出现在坝顶附近。
4.7 心墙地震应力计算成果
心墙静动叠加应力见图25和图26,沥青混凝土心墙静动叠加最大压应力为1.26 MPa,最大拉应力为0.12 MPa。
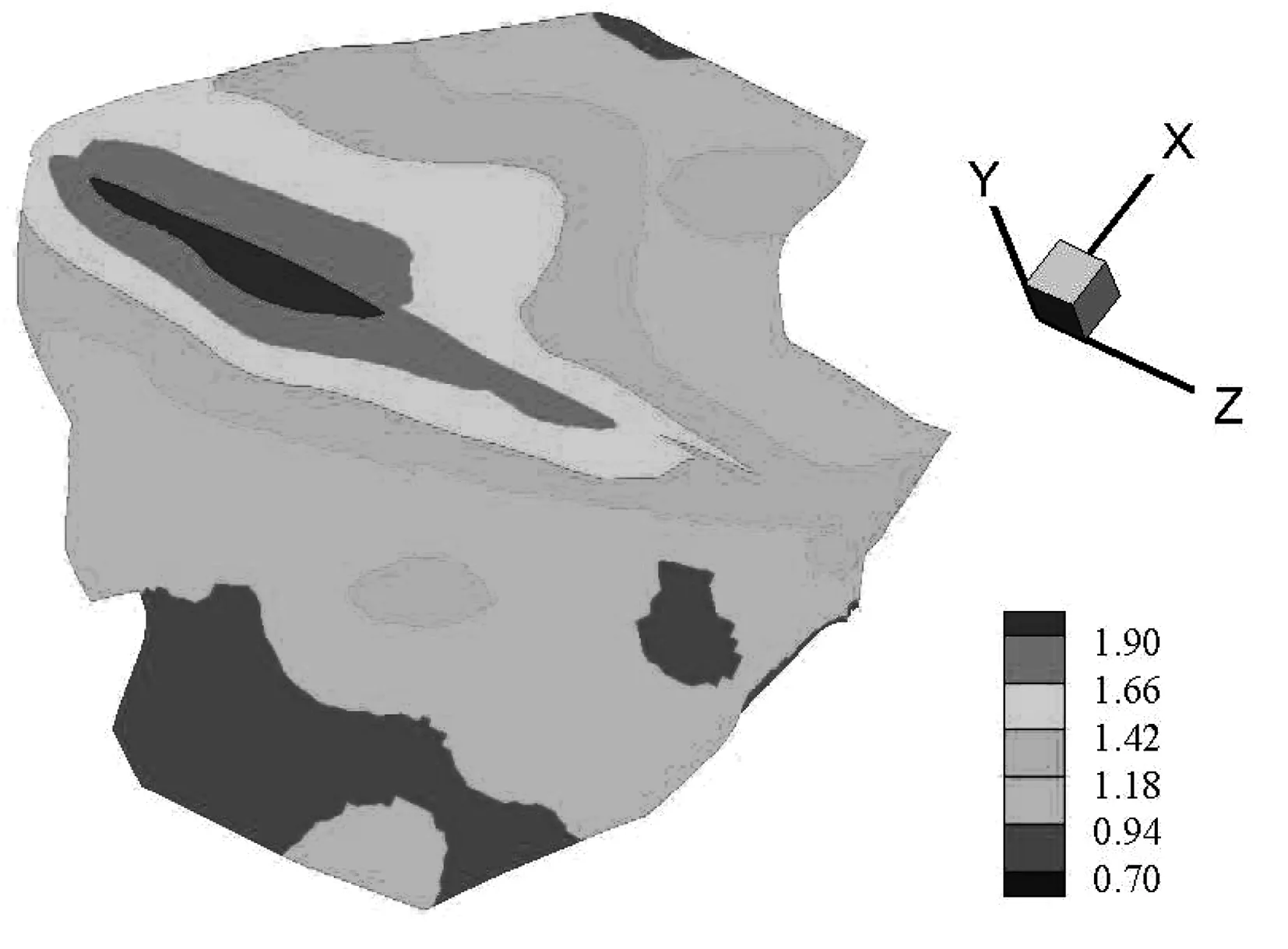
图23 大坝竖向最大动位移(cm)
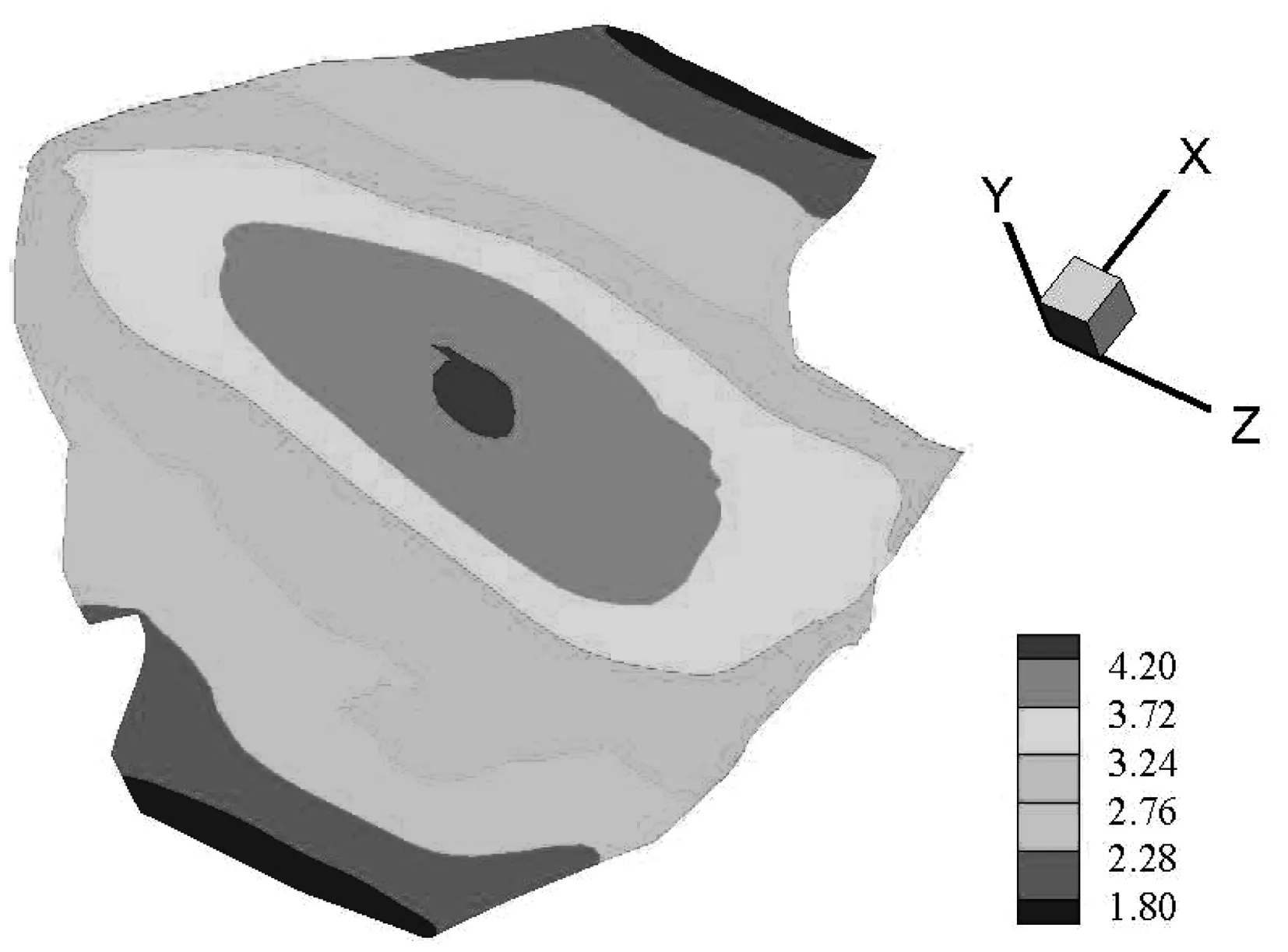
图24 大坝坝轴向最大动位移(cm)

图25 心墙静动叠加最大大主应力(MPa,压为正)

图26 心墙静动叠加最小小主应力(MPa,压为正)
4.8 心墙-基座地震相对位移
心墙与岸坡基座沿顺河向静动叠加最大错动位移为0.68 cm,位于坝体最大横断面附近。沿岸坡向静动叠加最大错动位移为1.35 cm,位于右岸靠顶部区域。
动力计算结果汇总见表7。

表7 动力反应极值
4.9 坝体和坝基永久变形
坝顺河向最大永久位移为1.60 cm(向上游)和4.80 cm(向下游);坝顶最大沉降为7.00 cm,约占坝高的0.09%。心墙最大压应力为1.05 MPa,无拉应力产生。坝体和坝基永久变形计算结果汇总见表8。

表8 震后大坝三维有限元计算极值
5 计算成果分析
通过上述计算成果分析可知,静力条件下,坝体最大沉降约占坝高的0.27%,蓄水后心墙最大压应力较竣工期减少约14.2%,蓄水后心墙顺河向最大位移较竣工期增大约2.6倍、沿坝轴线方向减小约13.3%;动力条件下,坝体地震沉降约占坝高的0.09%,地震发生时坝体最大横断面心墙出现拉应力,其值约为最大压应力的9.5%,地震结束后心墙最大压应力减小约16.7%,未出现拉应力,地震后坝体顺河向发生永久位移,心墙最大压应力较地震前增大1.9%,心墙顺河向最大位移较地震前增大约15.4%、沿坝轴线方向减小约11.5%。
6 结 语
综上所述,本文以新疆某水利枢纽工程为例, 采用500 kN和1 500 kN的高精度大型液压伺服静动两用三轴仪,分别采用固结排水剪试验方法、动剪切模量与阻尼比试验方法对新疆某水利枢纽工程筑坝材料进行了试验,分别测定了材料的静力试验邓肯张E-B模型参数、动剪切模量系数和指数、归一化的动剪切模量Gd/Gdmax和等效阻尼比λ和双曲线永久变形模型参数,采用非线性邓肯-张E-B模型进行大坝三维有限元静力计算,采用等效线性粘弹性模型进行大坝三维有限元动力计算,采用三维等价结点力法研究坝体地震永久变形,主要研究了坝体在静动力条件下坝体和防渗体受力机理。
本文所使用的研究方法和所得出的结论,可以作为其他类似高地热隧道设计的对比和参考依据。
——以淮南矿区为例

