基于熵指数与逻辑回归耦合模型的滑坡灾害易发性评价——以蓝田县为例

李利峰， 张晓虎， 邓慧琳， 韩六平

(1.贵州工程应用技术学院土木建筑工程学院，毕节 551700；2.贵州工程应用技术学院理学院，毕节 551700)

滑坡常发生在山区与丘陵地带，是最危险的地质灾害之一[1]。滑坡每年造成大量的人员伤亡与财产损失。据统计，世界上每年因滑坡造成的死伤人数约为1 000人，经济损失高达40亿美元，并且呈现逐年递增的趋势[2]。中国是一个滑坡灾害频发的国家，特别是在西北地区，由于环境恶劣以及人口集中，滑坡对当地居民生命与财产形成巨大的威胁。对每个滑坡的治理需要投入大量的人力与财力，在当前经济状况下并不具备可执行性。而对区域滑坡发生进行预测可以起到防灾减灾、指导工程部署以及合理规划土地等作用，具有重要的理论与实践意义。

目前，常见的滑坡易发性分析方法主要分为两大类：传统的统计学分析方法与机器学习法。传统的统计学分析法所建立的模型自变量的内部参数是由滑坡原始数据确定，可以避免人为因素的干扰，得到的参数结果更加客观，但在选取评价因子的过程中，更容易受主观因素的干扰。常见的传统的统计学分析法有层次分析法[3-4]频率比模型[5-6]、确定性系数模型[7]、证据权模型[8]、信息量模型[9]以及熵指数模型[10]等。机器学习模型可以避免各评价因子间互相依赖的问题，但由于模型的计算量大并且对模型参数的选取也较为困难，得到的评价结果很容易出现过拟合问题。最常见的机器学习算法有人工神经网络法[11]、支持向量机[12]、随机森林[13]、逻辑回归算法[14]等。

针对以上两类模型各自的优缺点，近年来，已有许多学者尝试将这两类模型进行耦合，形成混合模型应用于滑坡易发性评价中，并且取得了很好的预测结果。例如，谢洪斌等[15]利用模糊证据权法对汶川震区岷江流域雁门乡至映秀段滑坡灾害进行评价，得到较好的评价结果；安凯强等[16]将信息量模型与支持向量机模型相结合对三峡库区的滑坡灾害进行预测，将91.11%的滑坡预测为易发性高的区域。因此，将熵指数(index of entropy, IOE)模型与逻辑回归(logistic regression, LR)模型相耦合，形成IOE-LR模型并用于蓝田县滑坡灾害易发性评价中。该模型既可以避免评价因子在选取过程中受人为因素的干扰，又可以减少机器学习过程中出现过拟合的问题。但其不足之处是模型参数的选取是否恰当会直接影响滑坡预测结果可靠性。

1 研究区概况

蓝田县属于西安市辖县之一。地理位置为东经109°07′～109°49′，北纬33°50′～34°19′。东西长64 km，南北宽55 km，总面积2 007 km2。地形南北高、中间低，整体由东南向西北倾斜。区内最高海拔2 420 m，最低海拔397 m。按地貌单元将全县划分为河谷平原、山前洪积扇、黄土台塬、黄土丘陵和基岩山地5种地貌。蓝田县属暖温带半湿润大陆性季风气候，多年平均气温为13.1 ℃。境内河流众多，属黄河流域渭河水系，其中主要以灞河、浐河、零河及其支流水系为主。境内褶皱、断裂较为发育，新构造运动十分活跃，垂直差异性升降运动明显，进而增加了滑坡灾害发生的几率。人类工程活动主要有选址修房、开垦耕作、矿业开采、修建公路。全境在册滑坡点共有227处，其中土质滑坡占80.6%，岩质滑坡仅占19.4%。区内较为典型滑坡点以及研究区地理位置以及滑坡点分布图如图1、图2所示。

图1 姜湾村滑坡Fig.1 The landslide of Jiangwan Village

2 评价模型原理

2.1 熵指数(IOE)模型

熵指数模型是一种二元统计模型，它既可以单独对数据进行分类预测，也可以作为构建混合模型的输入数据。熵是指一个系统的不稳定或不确定性的程度。在滑坡易发性分析评价中，熵代表不同评价因子对滑坡灾害发生的影响程度。熵指数值越大，代表评价因子的影响作用越大，反之亦然。各评价因子的权重值由以下公式计算得到：

图2 地理位置以及滑坡灾害点分布Fig.2 Geographical location and landslide points distribution of the study area

(1)

(2)

(3)

Himax=log2S

(4)

(5)

(6)

Wi=Ii×Pi

(7)

式中：Pij为各评价因子分级的频率比；a与b分别表示对应分级的面积百分比与滑坡百分比；(Pij)代表概率密度；Hi、Himax表示熵值；S为评价因子分级数；Ii为评价因子信息率；Wi为评价因子权重。

2.2 逻辑回归(LR)模型

逻辑回归是一种用于二分类或多分类的分类预测模型。在滑坡易发性评价分析中，各评价因子作为模型的输入自变量，滑坡发生与否作为分类因变量(0代表滑坡不发生，1代表滑坡发生)。设P为滑坡发生的概率，1-P为滑坡不发生的概率，P的取值范围为[0,1]。P的表达式为

(8)

式(8)中：x1,x2,…，xn代表各评价因子；β1,β2,…，βn为逻辑回归系数；α为常数项，表示在不受任何有利或不利于滑坡发生因素影响的条件下，滑坡发生与不发生概率之比的对数值。

对P/(1-P)取自然对数，得到逻辑回归方程为

(9)

式(9)中：Z为滑坡发生概率的目标函数。

2.3 逻辑回归与熵指数耦合(LR-IOE)模型

上述IOE模型得到的Pij具有相同的维度，可以避免出现滑坡灾害点与评价因子间出现线性相关的问题以及在建模过程减少噪声的出现。将各评价因子按照Pij进行重分类，将Pij作为逻辑回归模型中的输入数据，构建LR-IOE模型，计算得到混合模型下的α与β。

3 评价因子的选取与分析

3.1 数据来源

用到的数据主要有滑坡点属性数据、各评价因子属性数据。其中滑坡点属性数据主要是通过收集的历史滑坡数据、野外调查以及卫星影像遥感解译等手段获取；各评价因子属性数据是通过ArcGIS软件对各评价因子图层提取获得。

3.2 评价因子选取与图层制作

在对蓝田县境内的地质环境条件、滑坡发育特征、形成条件等分析的基础上，初步选取高程、坡度、坡向、曲率、降雨量、距水系距离、地层岩性、距断层距离、距道路距离、归一化植被指数(normalized difference vegetation index,NDVI)共10类影响因素作为评价因子。利用ArcGIS软件提取各因子图层，如图3所示。其中，高程、坡度、坡向、曲率图层主要提取自30 m×30 m分辨率的数字高程模型(digital elevation model,DEM)影像；降雨量图层通过蓝田县气象站点数据经克里金插值获取；地层岩性、断层、水系、道路图层分别通过对1∶50 000地质图、水系图、路网图进行矢量化，并转为栅格得到。

图3 评价因子图层Fig.3 Evaluation factors layer

3.3 评价因子多重共线性分析

对研究区进行滑坡易发性评价时，评价因子选取的数量与质量都会影响评价结果。因此，并不是所有的评价因子对评价结果都能产生积极作用。当评价因子间存在多重共线问题时，不仅会增加模型的复杂度，而且会出现模型过拟合问题，大大降低模型的泛化能力，降低预测结果的准确度。因此，分别采用皮尔森相关系数(Pearson correlation coefficient，PCC)、方差膨胀因子(variance inflation factor，VIF)以及容忍度(tolerance，TOL)3种指标分析因子变量之间的多重共线性。

PCC常用来反映变量间的线性相关性，其绝对值越大，说明变量间的多重共线性越强。假设有样本数据集(Xi,Yj)=(x1,y1), (x2,y2),…,(xn,yn)，变量间的线性相关系数PCC的计算表达式为

(10)

一般认为，当0≤∣PCC∣≤0.3时，变量之间呈低度相关；当∣PCC∣>0.3时，变量之间相关度较高。

VIF与TOL也是判断变量间是否多重共线的重要指标。VIF是将存在多重共线性时回归系数估计量的方差与不存在多重共线性时回归系数估计量的方差对比而得出的比值系数。TOL为VIF的倒数。通常认为，当00.4时，表明变量间多重共线性较弱，当VIF>2或TOL<0.4时，表明变量间多重共线性较强。

对各评价因子的多重共线性进行分析，得到的结果如表1、表2所示。由表1可知，各评价因子之间相关系数的绝对值均小于或等于0.3，表明各因子间相对独立；由表2可知，各评价因子的VIF值均小于2，TOL值均大于0.4，表明各因子之间多重共线性较弱。

3.4 评价因子分析

对各因子分级是进行统计学分析的前提条件。根据滑坡灾害点在区域分布的空间特征以及查阅相关区域文献，对各评价因子进行分级，得到各评价因子的分级状态，如表3所示。其中，坡度、坡向、距断层距离、距水系距离以及距道路距离按照相等间隔法划分；高程、曲率、NDVI、降雨量按照自然间断点法划分；地层岩性分类编号如下：1(太古界太华群)、2(下元古界陶湾组)、3(中元古界秦岭群)、4(古近系与新近系砂泥岩)、5(第四系风成黄土)、6(第四系全新统冲积层)、7(第四系全新统洪积层)、8(加里东期花岗岩)、9(燕山期花岗岩)、10(喜山期花岗岩)。采用频率比法对各评价因子与滑坡点的空间分布关系进行分析，得到各因子的频率比如表3所示。

从表3中可以得出，高程在782～1 084 m，坡度在8°～24°，坡向为朝东或西南方向，曲率为0.44～0.12的凸型坡，其频率比值相对较大，说明在此地形条件下滑坡灾害最容易发生。断层、水系与道路随着距离的增加，中间稍有起伏波动，但总体呈现出频率比值逐渐减小趋势，说明距离水系、断层、道路越近，越容易诱发滑坡。NDVI在0.02～0.07范围内，频率比最大，说明滑坡多发生于植被较少的区域。

4 滑坡易发性评价

将整个研究区按照30 m×30 m栅格大小进行划分，共划分为2 230 784个评价单元。利用ArcGIS软件里的栅格转点工具提取研究区各图层的属性值，建立研究区属性数据库。利用多值提取至点工具提取滑坡点各因子属性值，建立滑坡属性数据库。

4.1 熵指数(IOE)模型

根据式(1)～式(7)，利用Excel软件求得的各评价因子权重值如表3所示。最终的滑坡易发性区划图由以下公式求得：

(11)

式(11)中：LSIIOE表示滑坡易发性指数；i表示评价因子数；e表示分级数最多的评价因子的分级数量；fi表示各评价因子的分级数；C为各评价因子分级后重分类值。

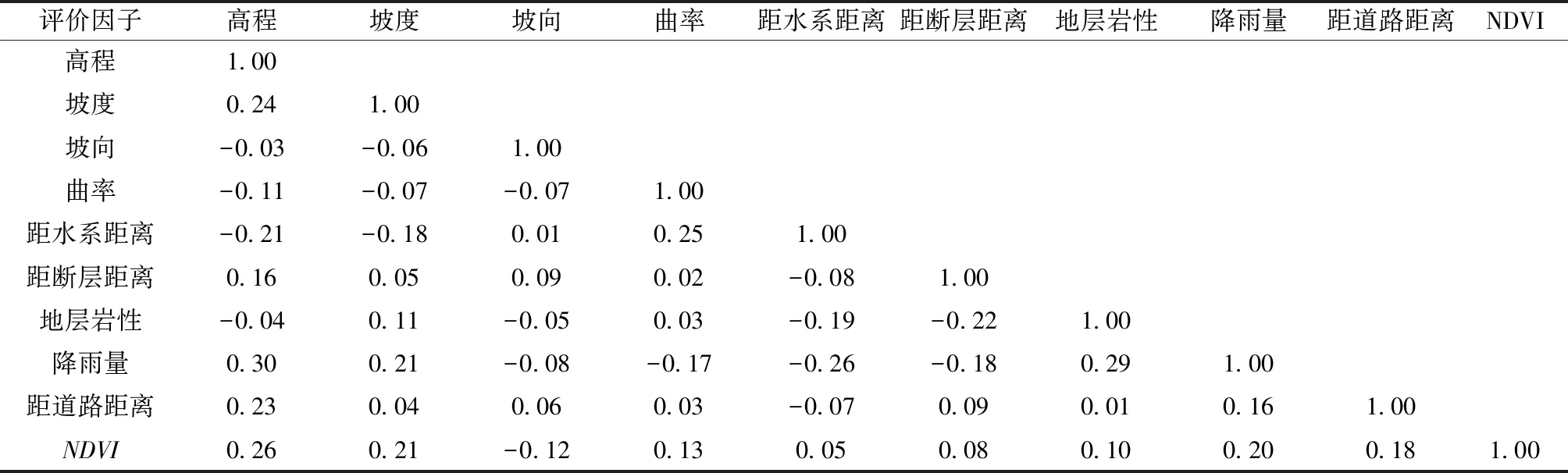
表1 评价因子之间的皮尔森相关系数Table 1 PCC between factors

表2 评价因子的方差膨胀因子与容忍度Table 2 VIF and TOL for factors

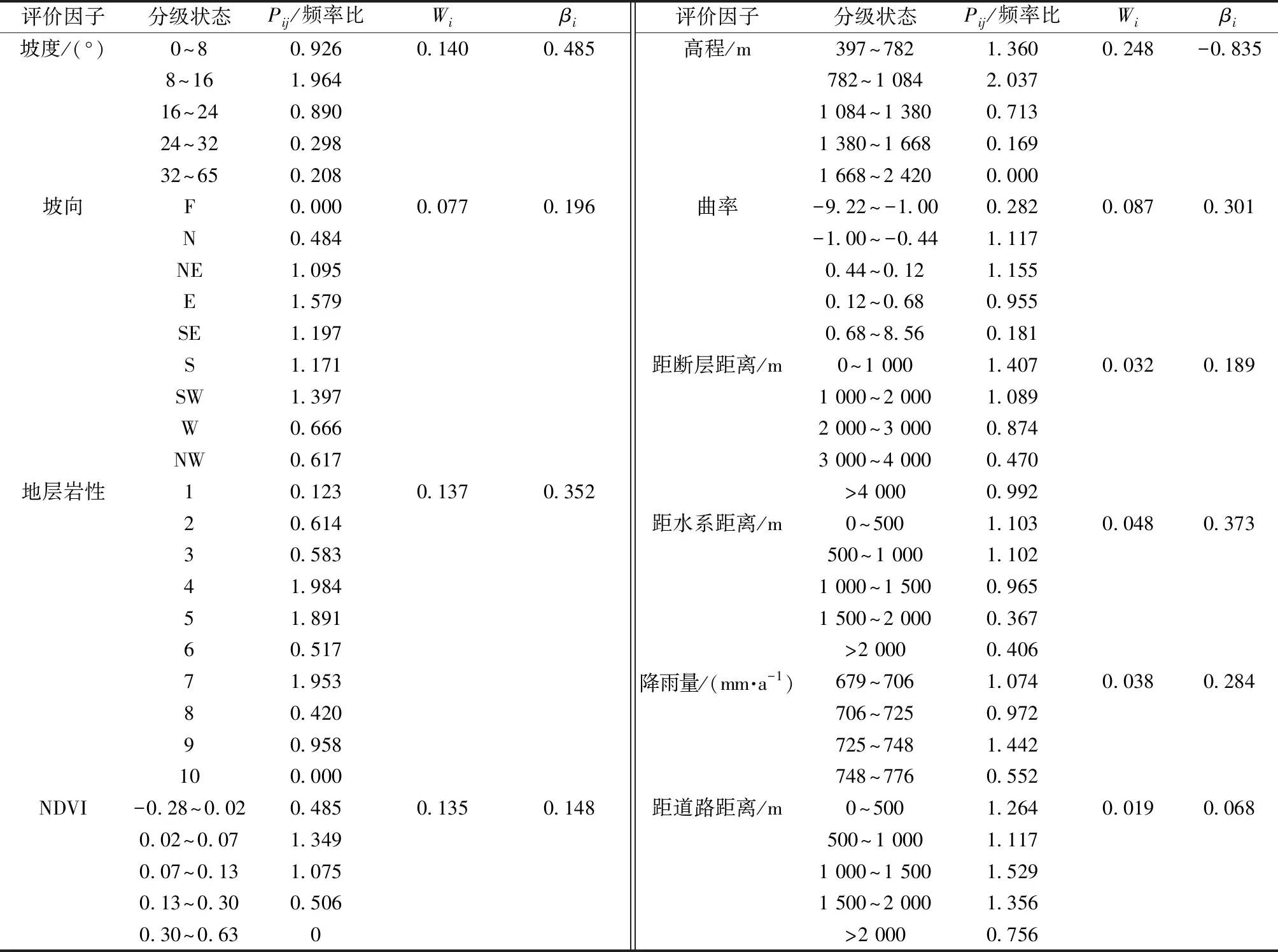
表3 评价因子与滑坡点空间分布关系Table 3 Spatial relationship between each factor and landslide

利用式(11)，求得区域的易发性指数LSI范围为2.41～9.48。LSI越大，表示滑坡越容易发生，LSI越小，表示滑坡发生的概率越小。采用自然间断点法将LSI分为5个等级，分别为极低易发等级(2.41～4.63)、低易发等级(4.63～5.65)、中易发等级(5.61～6.71)、高易发等级(6.71～7.68)、极高易发等级(7.68～9.48)，生成最终的滑坡易发性区划图，如图4所示。其中，极高-高易发区占研究区面积的45.3%，滑坡占总滑坡数的86.5%，滑坡点密度为0.216个/km。

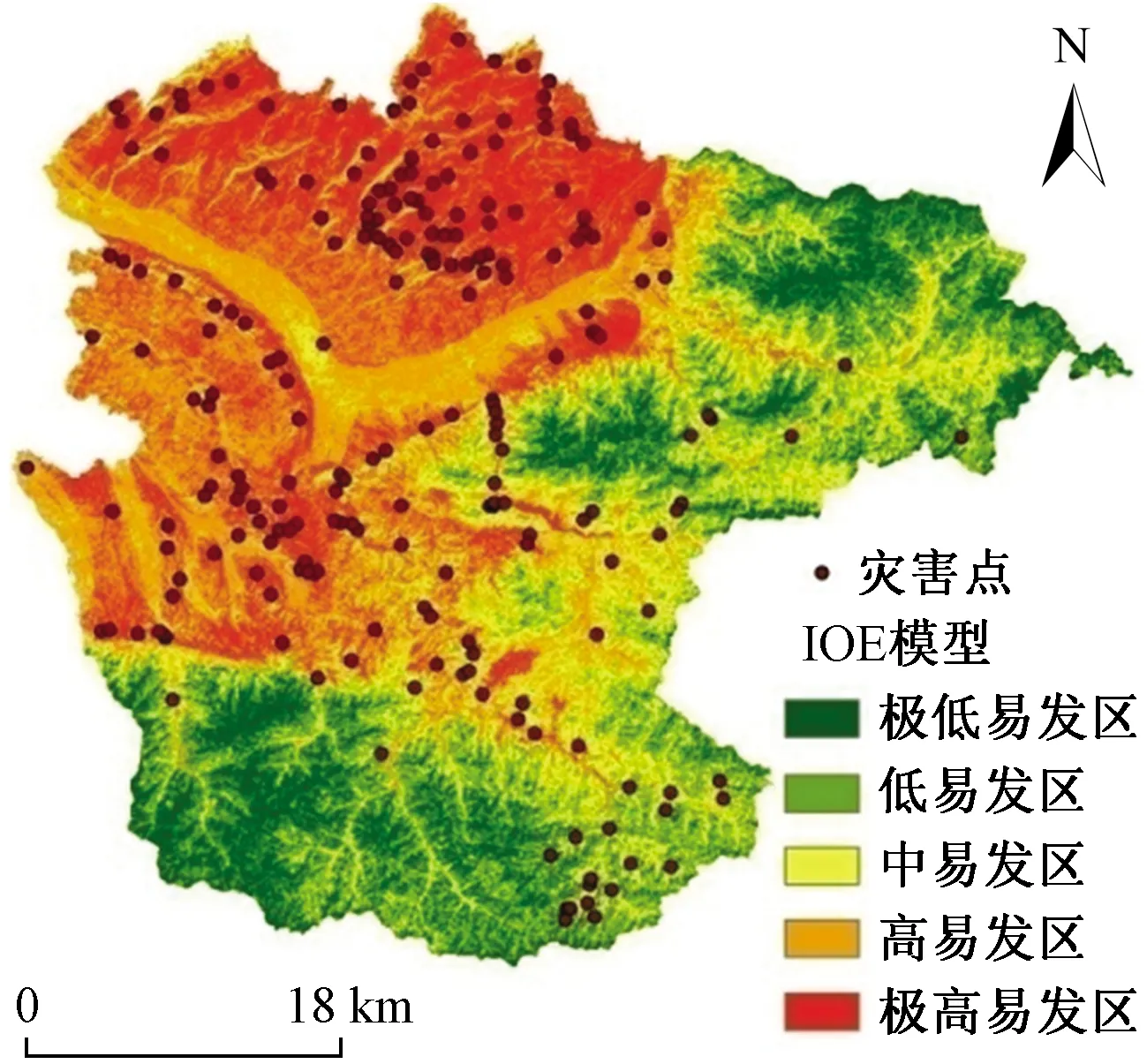
图4 基于熵指数模型的研究区滑坡灾害易发性区划图Fig.4 Landslide susceptibility mapping based on IOE model in study area

4.2 逻辑回归(LR)模型

将滑坡点与随机选取的相同数量的非滑坡点组成总的训练样本集，从总训练样本集中随机选取70%的滑坡点与相等数量的非滑坡点，共计318个作为训练样本集，剩余的作为测试样本集。采用R语言里的逻辑回归对训练样本集进行学习，再将学习得到的模型用于测试样本集，得到模型的预测正确率为82.5%；随后将研究区属性数据库代入训练好的模型中，得到研究区的滑坡灾害易发性指数LSI，将LSI按自然间断点法分为5个等级，分别为极低易发等级(0～0.16)、低易发等级(0.16～0.40)、中易发等级(0.40～0.52)、高易发等级(0.52～0.64)、极高易发等级(0.64～0.93)，生成最终的滑坡易发性区划图，如图5所示。其中，极高-高易发区占研究区面积的38.4%，滑坡占总滑坡数的84.3%，滑坡点密度为0.248个/km。

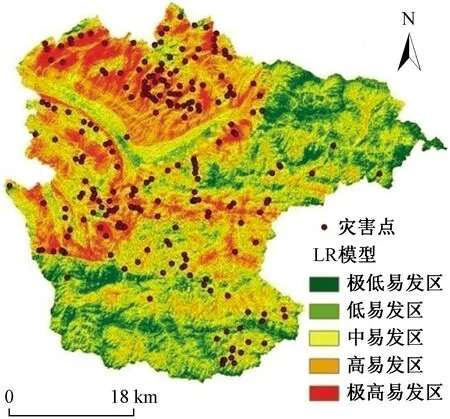
图5 基于逻辑回归模型的研究区滑坡灾害易发性区划图Fig.5 Landslide susceptibility mapping based on LR model in study area

4.3 基于熵指数与逻辑回归耦合(IOE-LR)模型

将式(2)求得的Pij作为输入数据代入R语言的逻辑回归模型进行学习，最终得到模型的预测正确率为85.6%。对整个研究区进行预测，得到研究区滑坡易发性指数LSI，同样按照自然间断点法将其划分为5个等级，分别为极低易发等级(0～0.15)、低易发等级(0.15～0.31)、中易发等级(0.31～0.47)、高易发等级(0.47～0.65)、极高易发等级(0.65～0.97)，生成最终的滑坡易发性区划图，如图6所示。其中，极高-高易发区占研究区面积的30.4%，滑坡占总滑坡数的80.2%，滑坡点密度为0.298个/km。

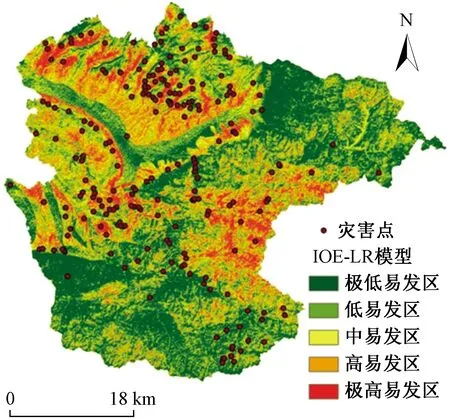
图6 基于熵指数与逻辑回归耦合模型的研究区 滑坡灾害易发性区划图Fig.6 Landslide susceptibility mapping based on IOE-LR model in study area

5 模型的检验与对比

采用ROC曲线对3种不同模型的性能进行检验与比较，用ROC曲线下的面积(area under curve,AUC)分别表示训练样本与测试样本的成功率与预测率，得到各模型成功率与预测率曲线如图7、图8所示。

图7 成功率曲线Fig.7 The success rate curve

图8 预测率曲线Fig.8 The prediction rate curve

IOE模型、LR模型、IOE-LR模型成功率曲线的AUC分别为0.735、0.742和0.805；预测率曲线的AUC分别为0.732、0.785和0.830，IOE-LR模型均有最高的成功率与预测率，表明IOE-LR模型整体要优于单一模型。

6 结论

分别采用IOE模型、LR模型、IOE-LR模型对蓝田县滑坡灾害易发性分析，取得以下结论。

(1)分别采用皮尔森相关系数、方差膨胀因子、容忍度3种指标对评价因子之间的多重共线性问题进行分析，结果表明，各选取因子之间多重共线性较低，可以认为各因子相对独立。

(2)IOE、LR、IOE-LR3种模型在极高-高易发区内滑坡点密度分别为0.216、0.24、0.298个/km。说明IOE-LR模型在极高-高易发区内滑坡分布更加集中。

(3)采用ROC曲线对3种不同模型的性能进行检验与比较，IOE模型、LR模型、IOE-LR模型成功率曲线的AUC分别为0.735、0.742和0.805；预测率曲线的AUC分别为0.732、0.785和0.830，IOE-LR模型均有最高的成功率与预测率，说明IOE-模型整体上优于单一模型。