瞬变电磁井间勘探的全空间几何因子
沈建国,李红瑞,沈永进
(1.天津大学微电子学院,天津300072;2.北京华晖盛世能源技术股份有限公司,北京101300)
油田开发过程中有大量剩余油因采收率低仍分布在井间区域,这些剩余油的准确评估和监测对石油开发具有重要意义。传统的单井测井技术横向探测深度浅,无法对井间区域进行有效探测,因此需要采用井间勘探方法[1-2]。现有的井间勘探方法包括井间地震法、井间直流电电阻率成像方法以及井间电磁成像方法等。井间地震法通过对比井间地层的地震资料,利用井间地层的地震波传播特性(反射和透射界面)来推测地层及其界面;井间直流电电阻率成像方法利用地层的电流分布测量视电阻率,具体为对阵列供电电极依次供电,然后记录测量电极的电位差,最后将测量电位差换算成视电阻率;井间电磁成像方法依据电磁感应原理,直接测量井间地层的导电特性,然后反演得到井间电阻率分布的二维乃至三维图像,发射线圈多采用10~10000 Hz的单频信号。上述3种方法均存在多解性的问题[3],井间地震法由于地层对高频信号的强衰减,导致高频信号少、精度低;井间直流电电阻率成像方法需要在导电的泥浆中进行;井间电磁成像方法迭代次数多,计算难度大。
本文研究的井间瞬变电磁勘探方法,通过将发射线圈和接收线圈置于相邻井中,采用瞬变电磁激发方法得到响应,其主要包括线圈之间直接耦合的响应信号和地层中涡流(激发电流)的响应信号。瞬变电磁激发的频谱中低频信号振幅大,接收的响应信号为连续瞬态波形,原始数据量大,携带的地层信息丰富。该方法研究涡流激发的有用信号时,借助了Doll电流环模型,计算过程比井间电磁成像方法快捷、直接且物理意义明确[4-14]。
1949年DOLL[15]在研究无限大均匀地层的电磁感应响应时提出了几何因子的概念。将地层视为一个个位于空气中闭合的导电环,发射线圈在其中激发感应电动势,该感应电动势产生涡流,涡流在空间任意位置再次激发响应。DOLL 仅计算了发射线圈轴线上涡流激发的响应,并将其表示为空间各地层电流环电导率的加权平均值,其权重称为Doll几何因子。Doll几何因子是在不考虑涡流环之间的影响的情况下得到的正弦激励的近似解,发射信号频率和地层电导率的增加会导致解的近似程度变差。采用瞬变激发方式得到的频谱是连续的(阶跃函数激发的频谱为1/f),频率越低振幅越大,信号以低频成分为主,这满足了Doll几何因子的近似条件,因此采用几何因子描述瞬变电磁法,可得到足够精度的勘探结果[15-16]。
在Doll电流环模型下,根据Biot-Savart定理可知空间任意点的有用信号是空间各点地层电导率的加权平均值,该权重称为全空间几何因子,利用该几何因子可以分析井间瞬变电磁勘探中有用信号的响应特征,以及不同位置的接收线圈测量的涡流激发响应与空间各介质电导率之间的关系。本文利用不同的切面和立体图全面展现了三维全空间几何因子,并给出了瞬变电磁响应和有用信号响应的波形。
1 井间勘探的全空间几何因子
井间瞬变电磁勘探得到的响应可以通过Maxwell方程组求得,响应包含相互叠加的直接耦合信号和地层涡流激发信号。瞬变电磁勘探利用的是地层涡流激发的信号。为分别得到直接耦合信号和涡流激发信号,实现二者的解耦,我们仿照Doll电流环模型,利用电磁感应原理、磁通量和毕奥萨法尔定理直接计算地层涡流激发的信号,进而获得全空间几何因子和地层涡流激发信号响应的计算公式。



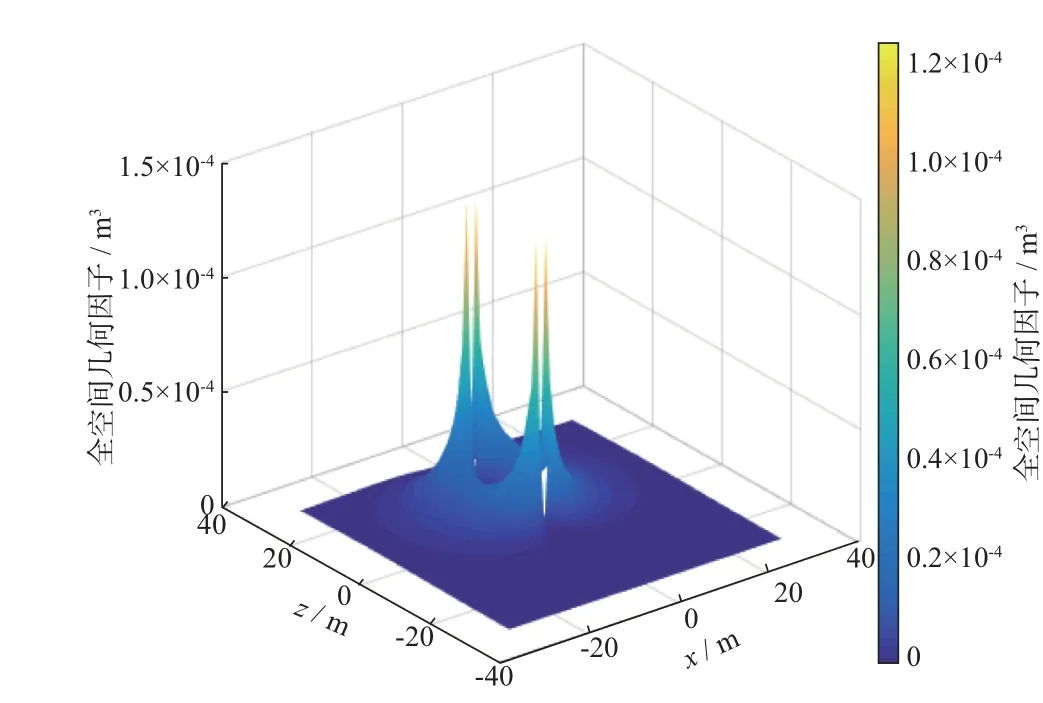
图2 全空间几何因子计算结果

图3 单个点的Doll几何因子三维显示
将全空间几何因子(对整个涡流环圆周积分以后的结果)除以2πr之后得到如图3所示的单个点的Doll几何因子,其形状与图2完全相同,这证明了全空间几何因子计算结果的正确性,值得注意的是,因Doll几何因子在极坐标下径向只有正值,故图3仅仅显示了一半的结果。
2 全空间几何因子的形态
全空间几何因子的自变量是x,y,z,因变量是全空间几何因子g,我们利用切片来显示全空间几何因子的形态。以下所有图件中发射线圈的位置坐标均为(0,0,0)m,接收线圈的位置坐标均为(0,100,200)m。二者x坐标值相同,即发射线圈和接收线圈均在x=0的平面内;二者y坐标值相差100 m,z坐标值相差200 m。
不同z切面的全空间几何因子如图4所示。当z=21 m 或z=-21 m 时(z值较小,接近发射线圈),发射线圈位置附近出现一对全空间几何因子正、负峰值,正峰值位于发射线圈和接收线圈之间,负峰值位于发射线圈之外;随着z的绝对值增大,正、负峰值的绝对值均减小,正峰值向着接收线圈方向(向上)移动;当z=99 m 或者z=101 m 时(在发射线圈和接收线圈中间),正峰值移动到了发射和接收线圈的中间位置;当z=181 m 和z=221 m(z值较大,接近接收线圈位置)时,正、负峰值几乎同时出现于接收线圈的位置,面向发射线圈一侧(向下)为正峰值,另外一侧(向上)为负峰值,并且这两个峰值与z=21 m 和z=-21 m 时的两个峰值完全相同,即发射、接收线圈的全空间几何因子关于z=101 m 的平面对称分布。

图4 不同z 切面的全空间几何因子
不同y切面的全空间几何因子如图5所示。当切面在发射线圈附近时,发射线圈附近出现全空间几何因子峰值:y=-10 m 时(切面在发射线圈左侧),峰值为负;y=10 m 时(切面在发射线圈右侧、发射和接收线圈之间),峰值为正。同样,当y切面在接收线圈附近时,全空间几何因子在接收线圈附近出现峰值:y=90 m 时(切面在发射和接收线圈之间),峰值为正;y=110 m 时(切面在发射线圈和接收线圈之外),峰值为负;当y=49 m 或y=51 m 时(切面在发射线圈和接收线圈中间),峰值相对减小,峰值分布范围大。y切面的全空间几何因子在发射线圈和接收线圈之间为正值,在发射线圈和接收线圈之外为负值,峰值集中分布在发射线圈和接收线圈附近,并且关于y=50 m,z=100 m 呈轴对称分布。

图5 不同y 切面的全空间几何因子
不同x切面的全空间几何因子如图6所示。可以看出,x值较小时(切面距离发射和接收线圈较近)全空间几何因子绝对值较大,随着x值的增加,全空间几何因子绝对值不断减小,分布范围不断扩大且全空间几何因子值关于x=0的平面呈对称分布。
图7为z方向全空间几何因子三维分布及其模值等高面立体显示,发射线圈坐标为(0,0,0)m,接收线圈坐标为(0,10,20)m。从图7a可以看出,在发射线圈和接收线圈之间全空间几何因子为正值,在发射和接收线圈之外为负值,这个极性差异体现在y轴上,该值分布区域在发射线圈或者接收线圈两侧均呈对称关系。由图7b可知,随着观测区域与发射或接收线圈的距离不断增加,全空间几何因子模值由大变小。模值由大到小分别采用3种颜色(红色、绿色和蓝色)表示(注意:在发射和接收线圈之间(y轴方向)全空间几何因子值为正、剩下区域为负)。在发射和接收线圈附近的等高面为圆形,说明全空间几何因子具有对称性,其模值越小,等高面离线圈越远。在发射和接收线圈之间,全空间几何因子模值的等高面逐渐连为一体。这种规律在x切面、y切面和z切面上均有所体现。
对于沿z方向接收的涡流激发的响应,发射和接收线圈之间的地层引起的响应为正,发射和接收线圈之外的地层引起的响应为负,两者极性相反,这是磁场矢量造成的极性变化。全空间几何因子的模越小,其分布的区域越大,说明该区域的涡流对接收线圈的响应有贡献,接收线圈能够探测到该区域的地层电导率。
当接收线圈沿y方向放置时得到的(y方向)全空间几何因子分布如图8所示,从图8a可以看出,y方向的全空间几何因子主要集中在发射和接收线圈附近,发射线圈附近的绝对值大。全空间几何因子沿y轴的变化规律是发射线圈与接收线圈之间的区域其值为负,发射线圈之外的区域其值为正,接收线圈附近的值极性发生变化。全空间几何因子沿z轴的变化规律是发射和接收线圈之间其为负值,接收线圈之外的区域其为正值。模值从大到小分别采用3种颜色(红色、绿色和蓝色)表示,从图8b可以看出,模值越小,等高面离发射线圈和接收线圈越远;模值在接收线圈附近变化大。

图6 不同x 切面的全空间几何因子

图7 z 方向全空间几何因子三维分布(a)和模值等高面立体显示(b)
图9是接收线圈沿x方向放置时(x方向)全空间几何因子三维分布及其模值等高面立体显示。从图9a可以看出,x方向的全空间几何因子集中分布在发射线圈附近,在接收线圈附近的值很小;在发射线圈附近,全空间几何因子的极性沿x轴变化,x为负时全空间几何因子为正值,x为正时其为负值。如图9b所示,对沿x方向接收的全空间几何因子取模值,由大到小分别用红色,绿色和蓝色表示。全空间几何因子模值主要集中在发射线圈附近,接收线圈附近的模值很小。模值小时,全空间几何因子模值等高面连在一起,围绕着发射线圈分布,占据了大部分模值分布区域。

图8 y 方向全空间几何因子三维分布(a)和模值等高面立体显示(b)

图9 x 方向全空间几何因子三维分布(a)和模值等高面立体显示(b)
3 响应波形的数值模拟
如图10所示,将发射线圈和接收线圈置于不同的井中,数值模拟瞬变电磁激发响应波形和地层涡流激发的响应波形,其中发射、接收均处于无限大的均匀地层中,发射线圈和接收线圈平行于井轴放置,接收线圈接收z方向因磁场变化引起的感应电动势,轴线间距离为10 m,发射和接收线圈的垂直距离为30m。
图11为瞬变电磁激发响应波形,上升沿分别位于0,1500 ms处,下降沿分别位于300,900 ms处。

图10 井间瞬变电磁勘探的几何模型

图11 瞬变电磁激发响应波形

图12 不同地层电导率的响应(a)和响应差波形(b)
井间剩余油勘探主要研究波形中包含的地层电导率信息。根据发射线圈(磁偶极子)激发的磁场分布计算直接耦合信号,利用全空间几何因子计算有用信号,地层电导率分别为10,20,30S/m 时得到的响应波形如图12a蓝色虚线、橘红色虚线和黄线实线所示,3 个响应波形高度重合(见图12a 中的黄线实线)。上述结果说明,响应中与地层电导率无关的电接耦合的响应幅度大,地层电导率不同引起的响应差异小。将地层电导率为20,30S/m 的响应与10S/m的响应相减,去除直接耦合响应,仅剩下与地层电导率有关的有用信号的差,相较于总响应,得到的响应差幅度很小(图12b中绿色实线和紫色实线),包含正、负两个峰值,这是地层涡流再次激发的响应波形,其变化幅度与地层电导率的差呈正比,该响应差在瞬变电磁响应波形变化最快的位置分别取正、负极值,并且地层电导率差异越大,响应差的峰值幅度差异越大。
提取接收线圈的响应中第1个下降沿激发的有用信号响应,通过改变地层电导率和井垂直间距,得到如图13所示的3条曲线,可以看出,3种地层电导率的涡流激发响应幅值随着井垂直间距的增加单调地减小,3条曲线未相交。
取地层电导率为1S/m,发射线圈和接收线圈的轴线距离为10 m,接收线圈分别位于(垂直深度z为)5,15,25,35,45 m 时,移动发射线圈,计算z变化时各个接收线圈涡流激发响应的情况(图14),可以看出,在一同深度发射和接收时,涡流激发响应的幅度最大。随着发射线圈和接收线圈的距离增加,响应幅度减小。
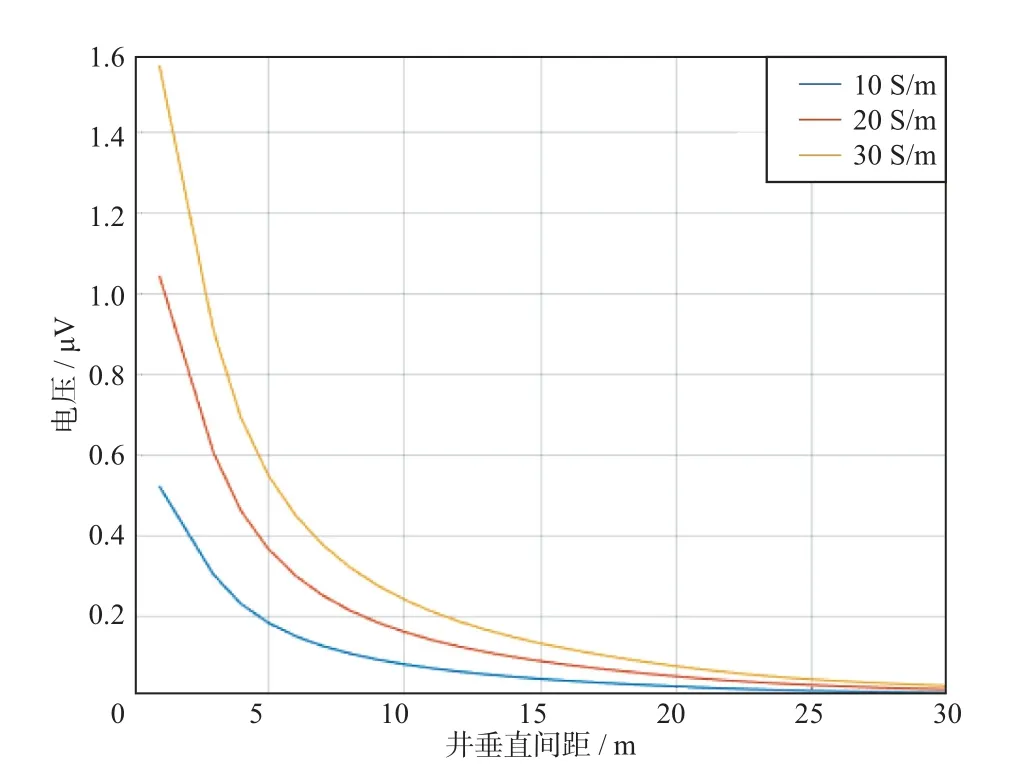
图13 不同地层电导率时涡流激发响应幅值随井垂直间距的变化情况
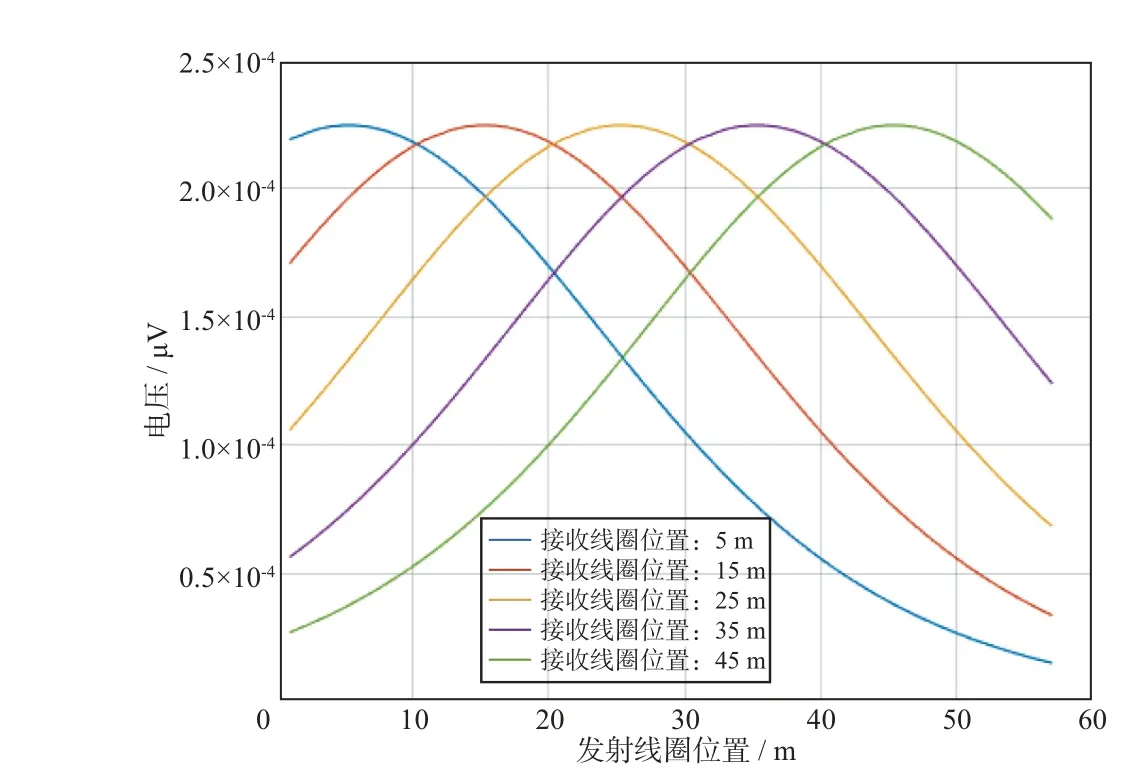
图14 发射线圈和接收线圈位于不同深度时涡流激发响应的变化情况
4 分析与讨论
利用线圈中的电流导通和关断激发瞬变电磁场,得到的频谱是连续的,包含一个从0 开始的频率段(理想阶跃函数的频谱是1/f),并且频率越低响应幅度越大。每个频率均可以视作一个正弦波激励,其有用信号的响应可以用Doll几何因子(发射和接收线圈同轴放置)或全空间几何因子(发射和接收线圈不同轴放置)进行近似描述。对所有的频率计算其响应,再通过Fourier变换即可得到瞬变电磁响应波形,作为一个瞬态响应,它包含了发射线圈激发的所有频率的响应。
DOLL在推导单频的感应测井响应(发射和接收线圈同轴放置)时,假设了地层电流环模型。该模型将地层视为无数个导电的圆环(地层电流环),根据空气中的电磁感应公式计算通过地层电流环的磁通量并获得感应电动势;该感应电动势在地层电流环中激发电流即涡流,该涡流会再次在接收线圈中激发感应电动势;再次激发的感应电动势与地层电流环的电导率呈正比,可描述接收线圈响应中的有用信号。发射线圈直接在接收线圈中激发的响应与地层电导率无关,是无用信号。Doll电流环模型及其理论推导结果给出了单频时响应的无用信号和有用信号,对所有频率的响应信号进行Fourier变换后可得到瞬变电磁响应的有用信号和无用信号。这相当于对瞬变电磁响应中的有用信号和无用信号进行了有效区分。
对于低频的瞬变电磁响应而言,Doll电流环模型具有足够的精度,因此,可以用于描述瞬变电磁的响应。与传统的地面瞬变电磁理论不同,根据DOLL的推导在理论上可直接区别有用信号和无用信号。
本文进一步将Doll电流环模型推广到井间且发射和接收线圈不在同一轴线上的情况,并将Doll几何因子扩展为全空间几何因子,使得井间瞬变电磁响应中所包含的地层电导率信息被有效分离,此外还给出了有用信号的正演计算方法。
5 结论
井间瞬变电磁响应中包含地层电导率的信息,它是地层涡流在接收线圈再次激发的电动势,可以用全空间几何因子进行描述,该电动势是空间各点电导率与该点的全空间几何因子乘积以后的积分。本文基于Doll电流环模型,推导了全空间几何因子和井间瞬变电磁响应中有用信号的表达式。数值计算结果展现了总响应和不同地层电导率时的响应差的关系,分析了不同地层电导率下,线圈在不同位置时有用信号形状和响应幅度的变化,得到如下结论:
1)全空间几何因子在发射和接收线圈附近最大,在发射线圈和接收线圈之间的空间范围内极性相同,线圈以外的空间范围极性反向。
2)全空间几何因子的模值越小,其分布的区域越大,且全空间几何因子是连续分布的。
3)瞬变电磁方法可以用于井间电导率分布的测量,其有用信号与地层电导率呈线性关系,可直接根据有用信号有效地识别地层电导率变化情况。
4)发射和接收在同一深度时涡流激发响应幅度最大,并且随着二者距离的增加,响应幅度变小。
本文提出的井间瞬变电磁勘探方法,为井间剩余油探测提供了新的方法。

