正则化形式的稳定粘声逆时偏移成像方法

冀国强，石 颖

（1.东北石油大学地球科学学院，黑龙江大庆163318；2.东北石油大学非常规油气研究院，黑龙江大庆，163318；3.陆相页岩油气成藏及高效开发教育部重点实验室，东北石油大学，黑龙江大庆163318）

在石油地球物理勘探中，深层偏移成像效果一直受限，其中主要原因就在于地层对地震波的吸收衰减效应。由于地下介质本身具有十分强烈的粘性特征，而传统偏移成像方法以胡克定律作为地下的岩石物理假设，与实际情况存在出入，因而导致成像结果出现偏差。

逆时偏移成像[1-3]以双程波动方程为理论基础，大幅度提高了叠前深度偏移结果的精确性和可信度，但是，由于早期所采用的波动方程均为没有考虑地下吸收衰减特性的声波或者弹性波方程，在实际应用中，该方法成像结果的分辨率与精确度不是特别理想[4]。

补偿因地层吸收而衰减的能量主要有两种方法。第一种是反Q滤波[5-6]，在偏移成像前直接对地震道进行反Q粘性补偿，该方法无论是在时域还是在频域都可以在一定程度上直接提高地震资料的分辨率。然而，振幅的衰减与相位的频散是随地震波的传播逐渐变化的，直接采用反Q滤波对地震道本身做补偿，忽视了地震波传播的几何特征[7]。第二种是在偏移成像过程中，对延拓的波场进行粘性补偿，采用具有粘性特征的波动方程进行延拓[8-10]，其中，粘性介质逆时偏移[11-13]由于其较高的精度，深受学术界与工业界的关注。

有两种方程被广泛应用于粘性介质逆时偏移。其一是基于标准线性体模型的带有记忆变量的波动方程[14]，其二是基于常Q模型的含有分数阶拉普拉斯算子的波动方程[14-16]。前者具有计算效率高、编程简便、易于实现等优势，只要将记忆变量的符号变负，便可实现对成像结果的补偿[17-18]。但是其振幅衰减与相位频散耦合，改变记忆变量的符号将会导致震源波场与检波点波场传播速度出现差异，使得成像结果同相轴发生错位[19-20]。而后者虽然需要利用傅里叶变换等方法求解分数阶拉普拉斯算子，增加了计算量，但是由于其振幅衰减项与相位频散项是分开的，仅改变振幅衰减项的符号，因而不会影响到震源波场与检波点波场的相位特征，传播速度一致，保证了成像结果中同相轴位置的准确性[12，21-22]。

然而，基于分数阶拉普拉斯算子的波动方程在进行振幅补偿的过程中，由于其补偿时间算子的补偿比例随着波数的增加呈指数上升，相当于一种高通滤波，会导致在延拓过程中高频噪声比例持续上升，最终淹没有效信号[12，19，23]。

对于高频噪声的压制，最初采用的方法是低通滤波，包括巴特沃斯低通滤波器[13]、Turkey窗低通滤波器[19]等，但是，由于这些滤波器滤波参数固定，在较长延拓时间后仍然会有部分高频噪声残留。许多学者对波场稳定性补偿传播进行了研究，XIE 等[24]提出了稳定性因子法，分别进行未衰减延拓以及衰减延拓，然后计算稳定性补偿因子，从而进行波场的精确补偿。田坤等[25]基于非相位频散粘声方程，提出了一种添加正则项的稳定性传播方程，避免了补偿不稳定问题。SUN 等[26]将稳定性补偿因子法拓展到成像条件，分别提出了两种稳定性补偿成像条件。GUO 等[27]将最小二乘理论中的Born近似理论用于计算粘性反传伴随方程，由于其具有衰减特性，不存在不稳定问题，然后根据反偏移计算等步骤获得经过补偿的成像结果。WANG 等[23]借鉴反Q滤波的思想，提出了一种自适应稳定传播算子。

本文提出了一种稳定性补偿策略，与田坤等[25]所提出的方法相似，均属于正则化方法，不同的是，本文所采用的粘声方程同时考虑了振幅衰减与相位频散。首先介绍了考虑吸收衰减效应的逆时偏移补偿原理，然后推导出正则化的稳定传播的粘声波动方程，最后进行两种模型的逆时偏移测试，对相位与振幅解耦的成像结果进行了比较，进一步验证了本文方法的实用性。

1 方法原理

1.1 粘声介质逆时偏移原理与成像条件

2.2 局部Marmousi模型

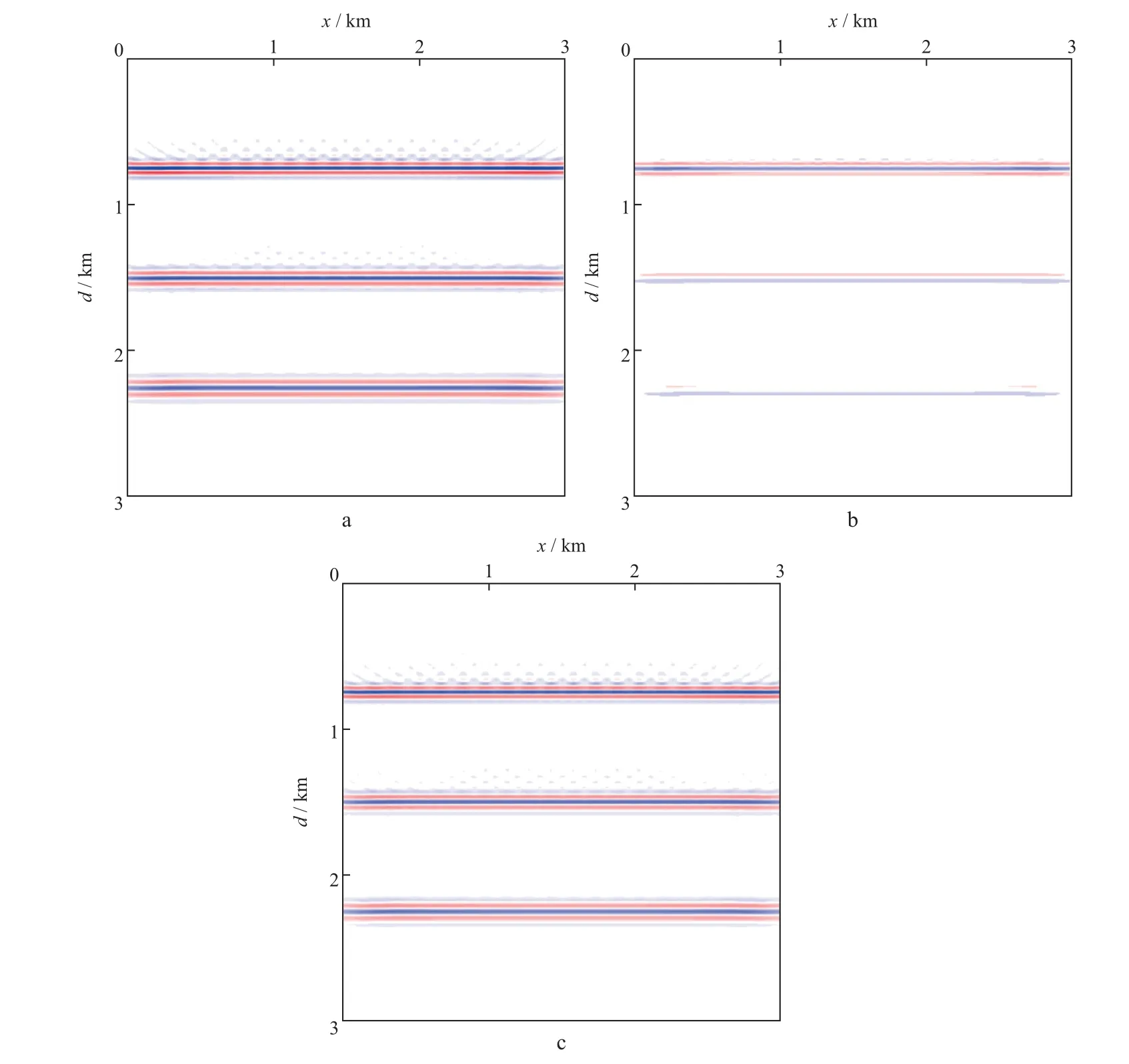
图3 水平层状模型成像结果

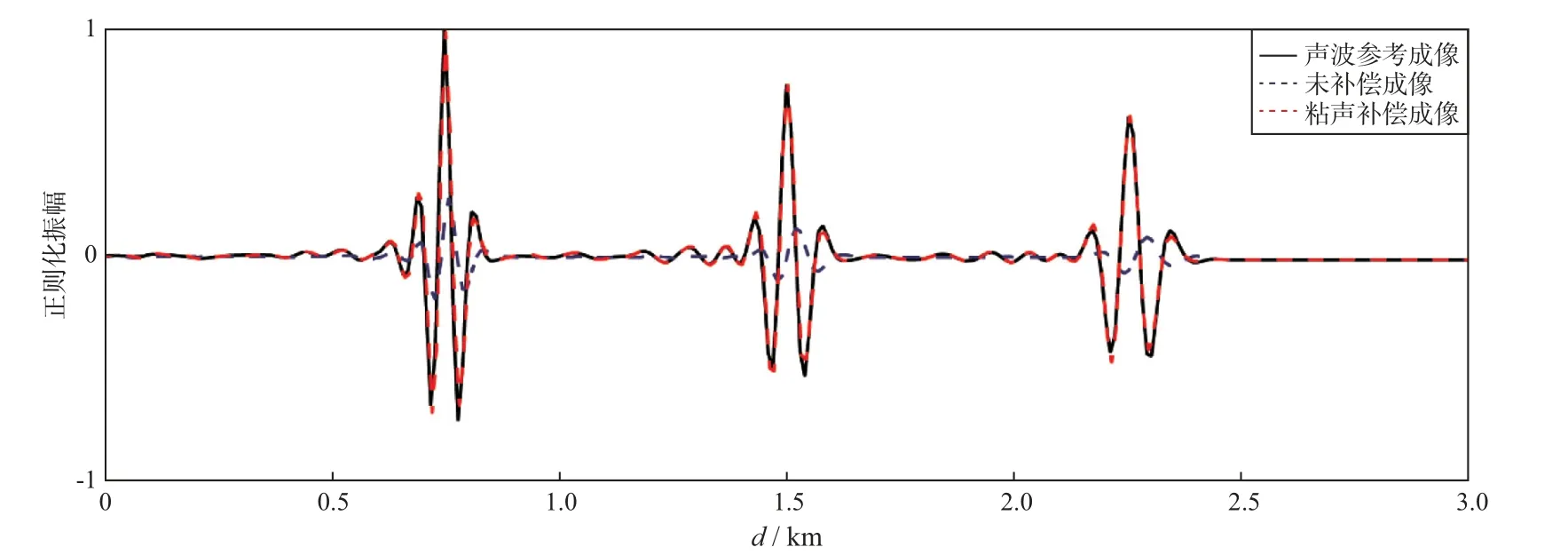
图4 水平方向1.5 km 处振幅曲线

图5 水平方向1.5 km 处曲线振幅谱

为了进一步验证本文方法在复杂情形中的适用性，从Marmousi模型中截取一部分进行成像测试，模型参数如图7 所示。模型网格大小为400 m×300 m，横向以及纵向网格间距均为10 m，从0 开始在地表均匀布置震源，炮间距为200 m，共20炮。采用检波点随炮移动接收的方式，检波点间距为10 m，共100个，炮两侧各放置50个进行接收。时间采样间隔为1 ms，记录长度为3s。成像结果如图8所示。

图6 相位与振幅解耦成像结果比较

图7 局部Marmousi模型

图8 局部Marmousi模型成像结果

由图8可以看出，在复杂模型的情况下，本文方法依旧可以得到理想的成像结果，相对于粘声数据声波逆时偏移结果，本文方法在保证了浅层成像效果的同时，深层成像更加清晰，由水平方向2 km 处抽取出的振幅曲线（图9）也可以进一步看出本文方法对于深层成像的优势。求取所抽取曲线的振幅谱，结果如图10所示，可以看出，本文方法对于复杂模型的频谱也有极佳的恢复与展宽效果。

图9 水平方向2 km 处振幅曲线

图10 水平方向2 km 处振幅曲线的振幅谱

3 结论

本文提出了一种正则化的稳定传播的粘声补偿方程，通过理论推导以及模型测试证明了本文方法的精确性和有效性，得出如下结论和认识。

1）通过对方程添加正则化项或者进行正则化处理，可以有效避免补偿过程中的数值不稳定问题，保证了补偿逆时偏移的有效性；

2）地层吸收衰减会同时影响地震波的振幅与相位特征，只有在进行补偿成像的过程中同时考虑这两种因素，才能保证最终成像结果的精确性与可信度；

3）采用互相关成像条件进行粘声补偿成像，需要对震源波场以及检波点波场都进行补偿处理，得到的结果无论是振幅还是频带都能够得到良好的恢复。

对于正则化参数的选取，本文暂不能提出一种量化的方式，这也是在今后需要继续探索的方向。