基于RS-PSO-SVM算法的腐蚀管道剩余强度预测技术研究

杨旭东，周艳丽，刘志娟，陆 亮，于天齐，刘 勇

中国石油天然气股份有限公司华北油田分公司第一采油厂，河北任丘 062552

近年来，我国油气管道呈现跨越式发展，截至2017年底，我国油气管道总里程超过12.5×104km。目前，我国大多数油气管道服役时间已超过20 a，因土壤、大气以及水体等多方面的影响，腐蚀成为危害管道安全、造成管道失效的重要因素，腐蚀缺陷不仅会引起管材的力学特性发生变化，而且会对管道的应力分布产生影响，因此，需要根据腐蚀情况对在役管道的剩余强度进行有效评价和预测，从而进一步判断管道是否需要降压运行或进入维修及更换阶段[1-2]。

目前，国内外相关学者已对腐蚀管道的剩余强度展开了大量研究。美国AGA管道研究委员会提出了基于断裂力学的NG-18环向失效应力计算公式，Kiefner等[3]以此为基础，提出了用于单一腐蚀缺陷剩余强度计算的B31G准则，后来美国ASME组织对其进行了多次修改，最为常用的是ASME B31G-2009版本[4]，此外挪威船级社制定了DNV-F101评价标准[5]，国内石油行业制定了SY/T 6151—2009评价标准[6]，这些评价标准可有效预测腐蚀管道的剩余强度，但普遍保守性强，容易造成对管道不必要的更换和维修。近年来，有限元分析成为计算管道剩余强度的有效手段，白清东[7]、Hoang Van Thanh等[8]均采用ANSYS对腐蚀管道进行了有限元分析，但该方法需要对不同的网格节点进行划分，对于工程实践来说，操作过于繁琐，一般人不易掌握。综上所述，无论是公式还是有限元分析，对管道剩余强度的计算都存在一定的弊端，且计算的数据与真实的水压爆破数据存在一定的误差，保守性过强，造成过早的更换管道，浪费资金。

随着机器学习、人工智能的兴起，利用相关算法实现对腐蚀管道剩余强度的有效预测是可行的。SVM（Support Vector Machine，支持向量机）是目前应用最为广泛的机器算法之一，可以有效解决小样本的分类和回归问题，但样本数据的准确性会影响预测的精度和鲁棒性，因此需要利用RS（粗糙集）属性约简理论[9]，对冗余和重复的影响因素进行筛除；而SVM中最重要的是惩罚因子C和核系数g的寻优，采用人工试算费时费力，可以采用改进的PSO（粒子群）算法[10]对参数进行寻优。因此，利用RS-PSO-SVM算法构建腐蚀管道剩余强度预测模型，可为管道完整性及延寿运行提供较好的理论依据。

1 研究方法

1.1 RS属性约简

RS（粗糙集）主要是利用二维信息表对信息进行有效表达，基本公式为S={U，R，V，f}，其中U为论域；R是属性的集合，R=C∪D，C和D分别为条件属性集和决策属性集；V=∪Vr是Vr属性值的集合，Vr为属性r的值域；f：U×R→V是一个信息函数，代表论域中的对象x的各种属性值。S={U，R，V，f}对应的二维数据即为决策表。

并非所有的条件属性都是必要的，在不影响决策属性的前提下，利用属性约简去除掉冗余信息，可以有效降低后期计算的时间和对噪声处理的困难。对于S={U，R，V，f}，设r0∈R，如果IND（R-{r0}） =IND(R)，则称属性r0在R中是冗余的，r0为冗余属性；反之，r0为必要属性。

1.2 改进的PSO

PSO属于仿生算法，根据鸟类捕食经验而来，通过群体中不同个体（n个粒子）的互相协作和信息共享来实现寻求最优解，PSO被广泛用于神经网络、遗传算法、模糊理论等算法优化和参数寻优。标准PSO的算法流程如下：

（1）初始化所有粒子并评价每个粒子的适应度，包括粒子的随机位置向量和速度向量。

（2） 与局部最优位置pbest进行比较，如果较好，选择pbest位置。

（3） 与全局最优位置gbest进行比较，如果较好，选择gbest位置。

（4）根据下面两个公式不断调整粒子的位置和速度向量：

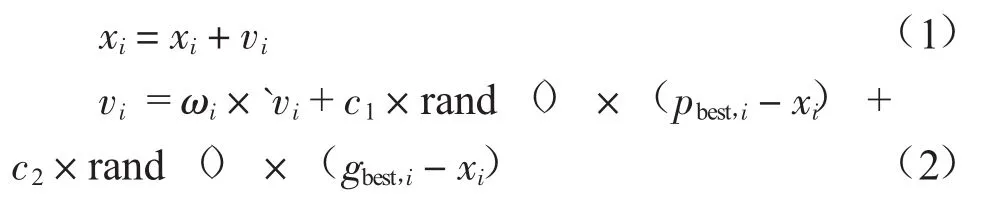
式中：xi为当前粒子位置；vi为当前粒子速度；ωi为惯性因子；c1、c2为学习因子，取值2；rand（）为（0，1）之间的随机数。

（5）当达到设置的最大迭代次数或寻求到最优解时停止计算，否则返回第（2）步。

在标准PSO计算中，惯性因子ωi采用线性递减方式，但会造成迭代后期局部搜索能力变差，因此采用非线性递减方式变化进行改进，公式如下：

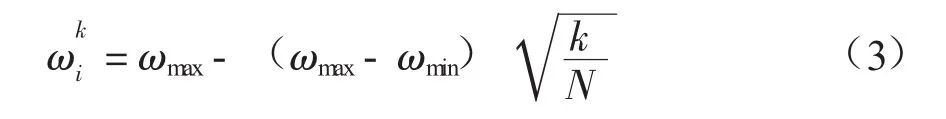
在标准PSO计算中，学习因子c1=c2=2，但实际c1和c2分别体现了对局部最优解和全局最优解的不断学习，随着迭代次数的增加，这两个值应为非线性变化而不是定值，c1应递减，c2应递增，因此引入余弦函数改进学习因子，公式如下：

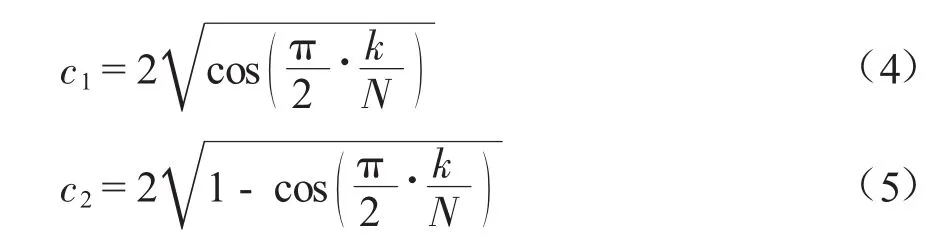
式中：c1、c2的取值范围为（0，2）。

1.3 SVM

SVM专门处理小样本条件下的非线性拟合和分类问题，对于腐蚀管道剩余强度预测问题，由于可查阅的真实水压爆破试验数据较少，因此可以利用SVM模型进行预测。基本原理是通过引入非线性函数，将低维空间的非线性拟合问题映射到高维空间中，并在高维空间中建立相应的模型进行线性拟合计算。拟合函数为：

式中：x为样本的输入向量；w为样本的权值向量；b为样本的拟合误差。

为了减少训练样本误差，引入了两个非负值的松弛变量ξ和ξ*，将上述公式转化为规划问题：

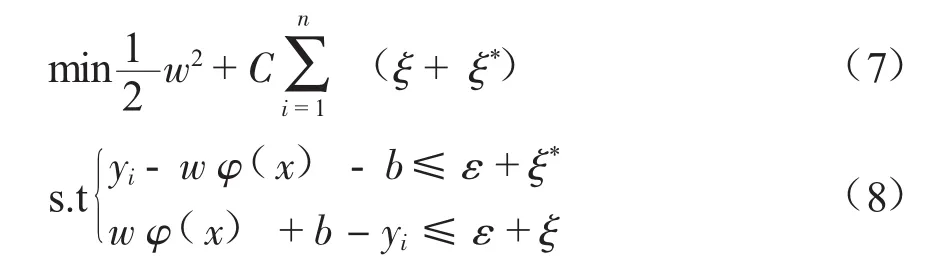
式中：C为惩罚因子；ε为不敏感参数。

引入拉格朗日乘子函数后，将上述的函数优化问题转化为对偶问题，整理上述公式后得到：

式中：ai和a*i为拉格朗日乘子，k（xi，xj） 为核函数。核函数的作用是将样本映射到高维空间中，常用的3种核函数分别是：多项式核函数、径向基核函数和S形核函数。研究表明：对于不同的数据类型，不同核函数表现不尽相同，径向基核函数在大多数数据处理方面表现优秀，因此，本文采用径向基核函数：

1.4 剩余强度预测模型

采用RS的属性约简理论，对剩余强度影响因素进行数据降维，将主要因素进行归一化处理后输入SVM模型进行训练，为了缩小误差，利用改进后的PSO对SVM中的惩罚因子C和核系数g进行寻优，最后建立RS-PSO-SVM算法的腐蚀管道剩余强度预测模型，预测流程如图1所示。

图1 腐蚀管道剩余强度预测流程

2 实例计算

2.1 数据来源

为了保证预测模型的准确性，采用文献[11]中79组真实的水压爆破试验数据，该组数据基本覆盖了X42～X100低强度到高强度钢级中常见的管道类型，将数据分为两组，其中随机抽取69组作为训练样本，剩余10组作为测试样本，采用平均绝对误差和均方根误差2个评价指标值分析模型的预测性能，公式如下：

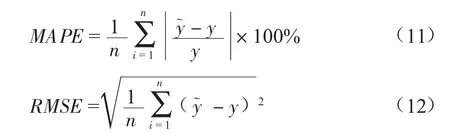
式中：MAPE为平均绝对百分误差；RMSE为均方根误差，MPa；为剩余强度预测值，MPa；y为水压爆破实际值，MPa。

2.2 指标体系构建

通过查阅相关文献，提取了影响腐蚀管道剩余强度的7项主要评价指标，分别是管道钢级、管径、壁厚、屈服强度、拉伸强度、缺陷长度、缺陷深度等，将剩余强度作为评价目标，构建了相应指标体系，如图2所示。

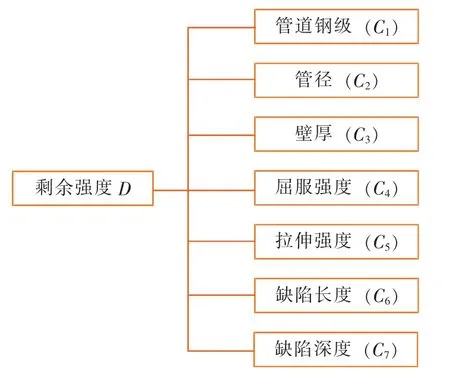
图2 腐蚀管道剩余强度指标体系

2.3 属性约简

将剩余强度按照由小到大分为4个等级，将文献[11]中的79组数据按照表1的标准进行离散化处理，得到剩余强度预测决策表，其中U为样本序号即论域；C={C1，C2，C3，C4，C5，C6，C7}为条件属性，剩余强度D为决策属性，将离散化的数据输入Matlab中进行编程，采用Johnson约简算法分析后得到约简条件属性集为{C1，C2，C3，C6，C7}，即降维后影响腐蚀管道剩余强度的主要因素有管道钢级、管径、壁厚、腐蚀深度、腐蚀长度。屈服强度和拉伸强度被去除，主要原因是这两者在剩余强度计算中主要影响的是流变应力，在管道钢级一定的情况下，屈服强度和拉伸强度的变化范围固定，流变应力也呈同趋势变化，因此管道钢级这一评价指标实际上包含了屈服强度和拉伸强度的大部分信息，管道钢级可以列入最优属性集中。

表1 腐蚀管道剩余强度指标离散化标准

2.4 参数寻优

由于各指标之间的单位和数量级都不尽相同，因此需要将属性约简后的指标进行归一化处理。将处理后的69组训练样本代入RS-PSO-SVM模型中，利用改进后的PSO对参数C和g进行寻优，其中设粒子数n=100，初始迭代次数N=0，最大迭代次数N=200，ωmax=0.8，ωmin=0.2，粒子维度D=1。分别对标准PSO和改进后的PSO进行对比，发现随着迭代次数的增加，两种模型的平均绝对百分误差都趋于最小值，其中标准PSO在175次迭代后达到收敛状态，平均绝对百分误差为2.101 2%，改进后的PSO在141次迭代后达到收敛状态，平均绝对百分误差为0.865 8%，可见改进后的PSO寻优和收敛速度更快，精度更高，具体见图3所示。此时的惩罚因子C和核系数g分别取85.914和0.765。

图3 标准PSO和改进PSO的平均绝对百分误差

2.5 预测结果及分析

随后再将剩余10组测试样本代入训练好的RS-PSO-SVM模型中进行预测，并利用mapminmax函数进行反归一化数据处理，为了更好对比和评价模型的准确性，与BP神经网络、PSO-WNN和ASME B31G的计算结果进行了对比，四种模型的预测结果如图4所示。

由图4可知，ASME B31G评价方法结果最为保守，与实际值拟合度最差，如采用该方法会造成管道过早地进行维修和更换，其余3种模型中RS-PSO-SVM的相关系数最大（R=0.999 93），证明可以预测99.993%的样本模型，只有总变异0.007%的数据样本不能被解释，与实际值的拟合度最高。除ASME B31G之外，其余3种模型的预测绝对误差对比见图5，平均绝对百分误差和均方根误差对比见图6。

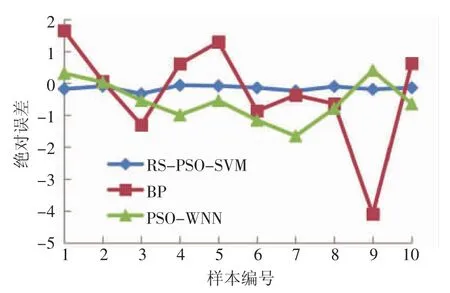
图5 预测绝对误差对比

图6 平均绝对百分误差和均方根误差对比

由图5和图6可知：从准确性分析——BP神经网络和PSO-WNN模型的预测绝对误差波动较大，RS-PSO-SVM的平均绝对百分误差为1.23%，均方根误差为0.17 MPa，均小于另外两种模型；与BP神经网络相比，RS可以很好去除高维数据的冗余信息；与PSO-WNN相比，SVM在精度上比WNN更适合管道剩余强度的预测。从保守性分析，RS-PSO-SVM、BP神经网络和PSO-WNN的预测结果中大于实际值的数据样本数量分别为0、5、2，由此可见，RS-PSO-SVM模型还具有较好的保守性。综上所述，几种模型相比，RS-PSO-SVM在维持保守性的同时，还能保持最大的准确性，因此该模型的泛化能力更强，预测准确度更高，可为腐蚀管道剩余强度预测提供安全、准确的预测数据。

3 结束语

（1）针对单一腐蚀缺陷管道的剩余强度样本数据少、公式计算保守性强、有限元分析过于复杂等特点，将RS、PSO和SVM算法模型有机结合，构建了腐蚀管道剩余强度预测模型。通过RS属性约简，有效提取了影响管道剩余强度的关键性指标因素，随后应用改进的PSO算法对SVM的参数进行了寻优，避免了人工试算法造成的误差和训练时间过长；与其余几种算法模型相比，保守性和准确性都较为优越，模型的鲁棒性和预测性更好。

（2）PSO算法同样存在容易陷入局部最优的缺点，今后可加强改进相关算法，提高算法寻优的准确性，减少训练时间。