基于最大系统容量的预编码算法

孙 会 楠

(哈尔滨华德学院 电子与信息工程学院, 黑龙江 哈尔滨 150025)

在无线移动通信系统中,多输入多输出(MIMO, multiple input multiple output)中继已经成为了一项关键的技术[1],它不仅可以有效增加系统容量和网络覆盖范围,而且能够降低网络架设成本.因为基站的复杂度和成本越来越高,使得在人口密集的城市或偏远地区通过部署大规模的基站来提高系统容量和用户通信质量的成本变得越来越高,MIMO中继技术能够以相对较少的投入,最大限度地提高用户的通信质量[2-4].采用中继传输技术在小区内部署一些功能相对简单的中继节点来转发基站和用户之间的信号,这样可以有效降低基站的发射功率,扩大基站覆盖范围、提高系统的通信速率.特别是放大转发(AF)中继,因为其具有低成本、低复杂度的特点,被普遍认为是最有发展前景的中继转发方式之一.本文研究的是在忽略基站和用户之间的直射信号的MU-MIMO中继系统中[5-6],如何对基站和中继节点进行合理的预编码矩阵设计.基于不同预编码矩阵设计准则下设计出预编码矩阵,然后简化系统模型,设计出基于最大化用户容量准则下的预编码矩阵,再得到采用不同算法的中继通信系统的用户总容量及误码率,以提高整个通信系统的性能.

1 最大系统容量的预编码算法

已知单个用户的用户容量计算公式为

式中,Ck为单位个用户容量,Sk为第k个用户的信干噪比.所以K个用户的总容量为

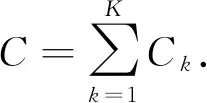
(1)

通过对基站和中继节点的预编码矩阵设计,提高通信系统的用户总容量.以最大化系统容量为准则,可以将问题转化[7]:

1.1 采用高信干噪比时对目标函数近似的方法

式(2)～式(4)的优化问题,我们能够运用MIMO固定中继系统的容量下限来进行求解.利用通信系统工作在高信噪比条件下对上述优化问题进一步简化,假设发送端已经获得了信道矩阵,首先对基站到中继的信道矩阵H1进行SVD分解[8],即

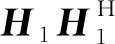
WB=V1ΛB.

(5)

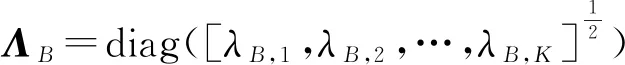
已知中继端的接收信号为[9]

yr=H1xB+nr=H1WBs+nr.

(6)

将式(5)代入式(6)中继端的接收信号也能够简化为

yr=U1Σ1ΛBs+nr.

因为系统的接收端为单天线用户,故中继的预编码处理矩阵WR为

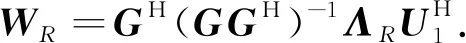
(7)

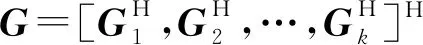
已知信号经过中继放大后为

xR=WRyr,

(8)

将式(7)代入式(8),中继节点的功率限制条件化简为

式中qk表示(GGH)-1矩阵对角线上的第k个元素.用户k接收到的信号可写为

用户k的信干噪比可以表示为

(9)

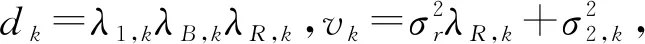
(10)

若S≫1,1+S能够近似于S,故通信系统工作在高信干噪比的情况下,能够将1+S简化为S,减小了整个算法的计算量,通过式(1)可知系统容量计算公式能够化简为

由式(11)可知,用户总容量C的最大值的求解等价于寻求信干噪比S倒数之积的最小值,把式(10)代入式(11)能够计算出在高信干噪比的条件下用户总容量为

为寻求系统容量的最大值就转换为如下问题的求解:

这就将对最大化系统容量的求解转变成对几何规划(GP,geomrtric programmaing)问题的求解.

几何规划最先是由 Zener于1961年研究工程设计中求最小值的最优化问题时提出的,直到1966年,Duffin等在文章中用到了“几何规划”一词,才被正式命名[10].在实际工程应用中,很多问题都可以把复杂的优化问题写成非线性规划的数学模型进行求解,而几何规划作为非线性规划一类特殊分支,应用也非常广泛,在求解具有大规模约束条件的优化问题时,几何规划算法有着很大的优势,同时还可以降低计算复杂度.

几何规划的标准形式为:

式中:fi为正定函数;gi为单项式函数;x为最优化变量.实际上,很多问题可以通过数学抽象转化为几何规划形式,因此对几何规划的求解发展十分迅速.为了简化对几何规划问题的求解,可以通过MATLAB中的GGPLAB工具包[11]或CVX工具包[12]来对几何规划最优解进行求解.

将式(12)进一步简化为标准的几何规划形式,然后通过使用MATLAB中的GGPLAB工具包对其进行仿真分析.

1.2 基于分步求解的预编码算法

在上一节中我们讨论了基于最大化系统容量准则, 利用系统在高信干噪比时对目标函数进行简化的方法, 联合设计基站及中继的预编码矩阵. 该方法利用系统工作在高信干噪比情况下时, 对需要求解的问题进行了一定的简化, 减小了求解的计算量, 然而如果使用该方法计算低信干噪比的情况下的用户总容量, 将会出现很大的误差. 为了解决这一问题, 我们可以使用新的分解算法, 对基站端和中继节点的预编码矩阵进行重新计算.

第一步,把中继节点的预编码矩WR阵分解成为2个部分:接收矩阵R和传输矩阵T,这相当于将信号在中继节点的传输分解成了2个独立的部分,这样就可以针对每一个的部分进行独立建模,然后再通过这2个独立部分的信道模型来求解预编码矩阵.

在分步求解的算法中,基站端和中继的预编码矩阵的形式和上一节一样.

等待他从那堆敝旧衣里爬出时，场坪里只有一个查验地摊捐的矮巡警笑咪咪的站在那里。因为观众只他一人，故显得他身体特别大，样子特别乐。

把WR分为2部分,即WR=TR,令

中继接收到基站端发送过来的信号为

yr=H1WBs+nr.

中继节点得到的信号首先通过接收矩阵R,经过R处理后的信号可写为

在最大化用户容量准则下,我们能够得出中继节点对信号进行接收处理这一步的目标函数和约束条件为:

利用注水定理进行求解得

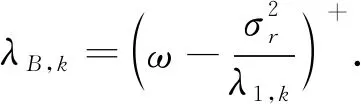
(16)

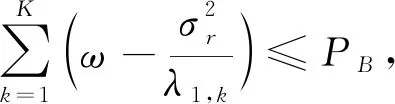
xrs=Tsr,

则用户k接收到的信号为

y2,k=GkTsr+n2,k,

(17)

将式(15)带入式(17),化简后可以得到

用户k的信干噪比S为

由最大化用户总容量准则,可将中继节点最优预编码矩阵设计问题转化几何规划问题

式中,qk表示矩阵(GGH)-1对角线上的第k个元素,对式(18)的求解可以当作一个求解拉格朗日极值问题,然后再运用拉格朗日乘子法对其进行求解,求得中继的最优功率分配因子为

式中,μ表示拉格朗日乘子[13-14],可以通过二分法对其进行求解,在求得μ之后再代入式(19)便得到了中继端的功率分配矩阵ΛR,再把ΛR代回式(14)就得到了最优的中继端的预编码矩阵WR.

2 仿真结果及分析

2.1 采用高信干噪比时对目标函数近似的方法的系统容量及误码率

利用高信干噪比时对目标函数近似的方法把目标函数和约束条件转化成了一般的几何规划问题,我们可以利用基于MATLAB的GGPLAB工具包对几何规划问题的最优解求解.图1和图2分别给出了用GGPLAB工具包计算在高信干噪比下对目标函数进行近似的系统容量和误码率(BER)曲线.由图1能够得出在低信干噪比的情况下对用户总容量的计算出现了很大的误差,之所以出现较大误差是因为对目标函数的近似是假设通信系统工作在高信干噪比的情况下进行的,因此低信干噪比情况下对用户总容量的计算很容易产生误差.故采用高信干噪比时对目标函数的近似的方法只适合于高信干噪比的情况下对用户总容量的计算.从图1还可以得出以下结论:随着信干噪比的逐渐增加系统容量随之线性增加,在高信干噪比的情况下系统容量要高于一般的线性预编码的系统容量 .从图2能够得知,信干噪比的增加会使得误码率下降,由于计算机的运算能力有限,在仿真时限制了基站端能够发送的比特数以及信道循环次数,故当信干噪比大于7 dB时系统误码率接近0.

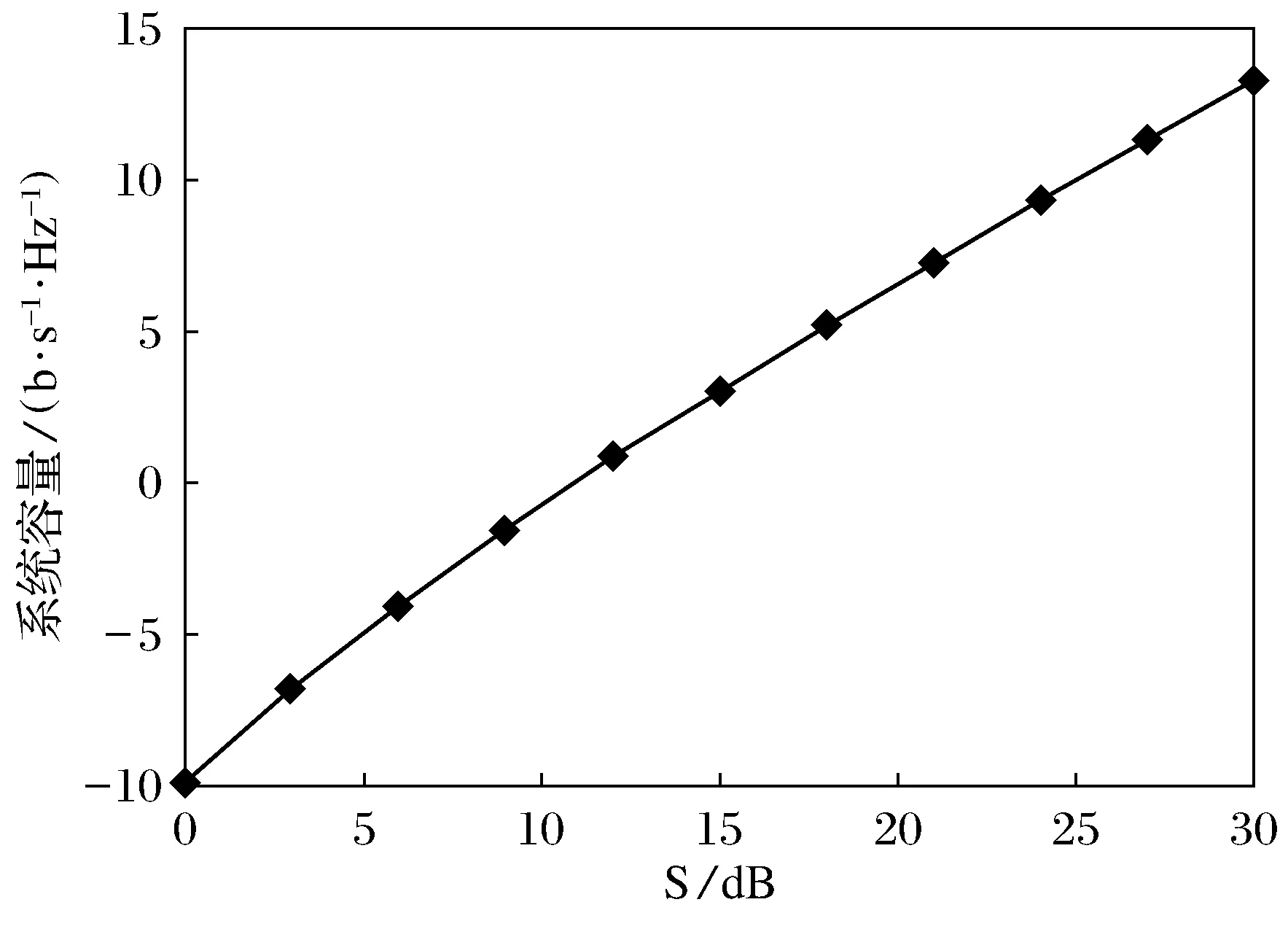
图1 采用高信干噪比时对目标函数近似的方法系统容量

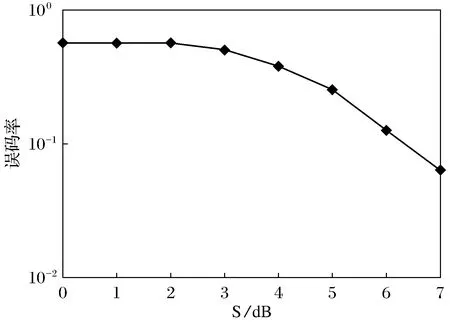
图2 采用高信干噪比时对目标函数近似的方法系统误码率

2.2 基于分步求解的预编码算法系统容量及误码率

如果通信系统工作在高信干噪比的情况下,采用对目标函数进行近似的方法能够有效降低运算量,但是如果通信系统工作在低信干噪比情况下,继续运用此法来计算系统容量就会出现较大误差,为了解决这一问题,提出了一种新的算法:基于分步求解的预编码算法.由图3可以看出用分步求解的方法来求用户总容量在低信干噪比时偏差较小,并且采用分步求解的方法来设计预编码矩阵对用户总容量的提升要优于采用高信干噪比时对目标函数的近似的算法.从图4可以看出采用分步求解的算法的误码率性能要优于采用高信干噪比时对目标函数的近似的算法.基于分步求解的算法不但能够提高用户总容量降低误码率,而且其算法复杂度要低于基于高信干噪比时对目标函数的近似的算法.

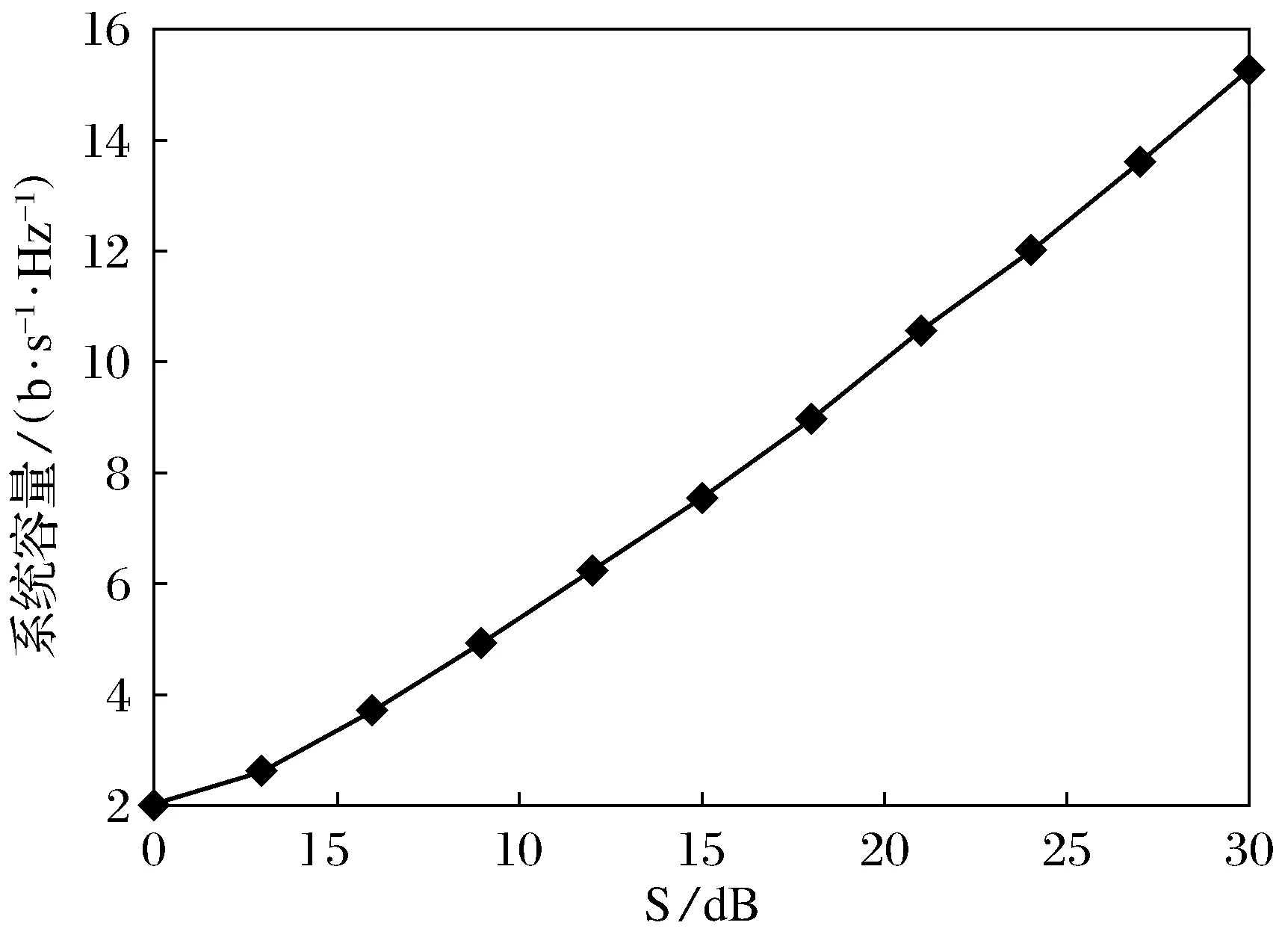
图3 基于最大化系统容量的分步求解的预编码算法系统容量

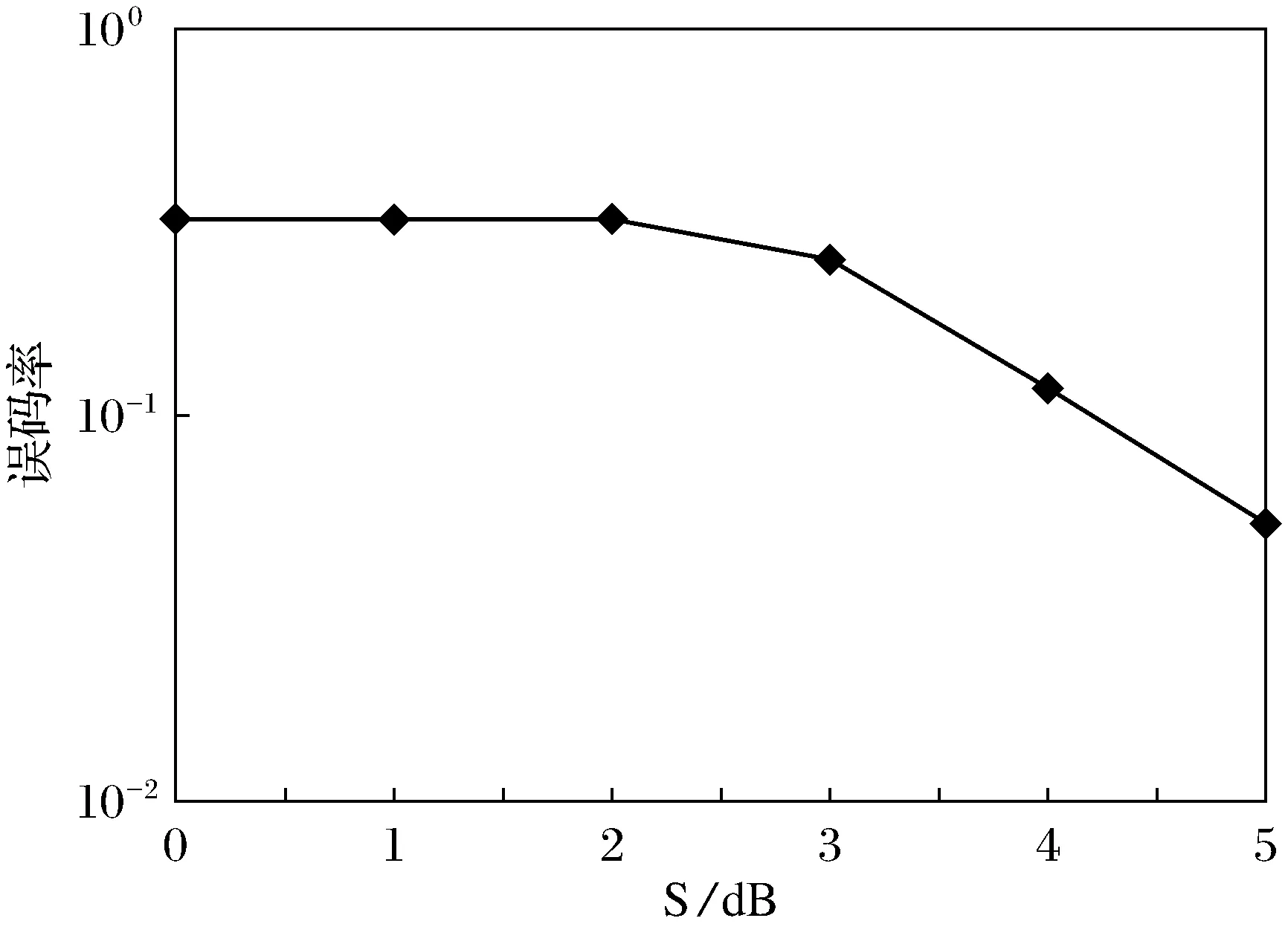
图4 基于最大化系统容量的分步求解的预编码算法系统容量

3 结 论

本文研究了在忽略基站和用户之间直接链路的MU-MIMO中继通信系统中,基于最大化用户容量的准则,采用高信干噪比时对目标函数近似的方法对基站端和中继节点进行最优预编码设计,从而抑制多用户之间的互相干扰,设计出能够使用户总容量最大化的预编码矩阵.这种方法虽然简化了对预编码矩阵求解的复杂度,但是如果通信系统工作在低信干噪比的情况下时,仍然采用该算法的话,将会对用户总容量的计算有较大的误差.为了解决高信干噪比时对目标函数近似的方法在低信干噪比条件下,对用户总容量的计算不理想这一问题,进一步引出采用分步求解的预编码算法,然后对该预编码算法进行了理论推导和数学分析,并对该算法在MATLAB软件中建模,采用GPPLAB工具包对基站端和中继的最优预编码矩阵进行求解.由仿真结果能够知道,在通信系统中运用分步求解的算法能够很好地改善运用高信干噪比时对目标函数近似的算法在低信干噪比情况下的对用户总容量计算出现偏差的问题,并且分步求解的算法还能够进一步提高系统的用户总容量,对最优预编码矩阵的求解的计算量也有所减小.