热量变化下含边裂纹TiC-Ni功能梯度条热应力影响
邹广平, Dergachova Nadiia, 王宇洋, 徐舒博, 唱忠良
(哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001)
功能梯度材料(functionally graded material, FGM)作为一种新型复合材料,其主要特点在于材料的组分和结构在一定空间连续梯度变化,同时,这种特性也决定了功能梯度材料能够承受极高的温度差,从而达到缓解结构热应力的作用.
目前,含裂纹的功能梯度材料热力学以及断裂行为问题引起了各领域科研工作者的关注[1-8].文献[9]利用理论和实验相结合的方式研究了FG材料的断裂及疲劳的力学行为问题.文献[1,3-4]利用解析法研究了含裂纹的半无限大功能梯度材料在热载荷下的热应力问题,并且通过分析边缘裂纹的应力强度因子,验证了文章结果的可靠性.文献[2,5]中分析了含边缘裂纹的功能梯度材料的准静态问题,其研究方法主要可以归纳为以下2种:傅里叶变换法和分层思想.文献[6]中对含混合裂纹的非均质正交各向异性材料进行了深入分析,发现了应力强度因子会因材料的不均匀参数的增大或者刚度比的减小而增大.文献[7]中通过温度加载实验,研究了在高低温循环加载下的含梯度涂层试件的裂纹开裂问题,同时也完善了温度循环加载下的裂纹开裂的规律:低温加载决定了垂直于顶层表面的裂纹起裂模式,随着温度的升高,引起了横向裂纹的扩展,最后由于裂纹扩展至覆盖层形成了层裂.
本文通过解析法计算功能梯度材料在指数升温加载以及线性升温[10]条件下,温度加载情况对功能梯度材料造成的不同影响.这个方法主要适用于一维[5,8]以及三维[11]情况的热应力研究.这种方法的优点是对于应力计算,它可以考虑功能梯度材料的所有物理性能参数的可变性质.最后,本文将所得到的结果和有效的实验分析结果进行了比较,二者符合得很好.
1 问题的描述
图1为热载荷作用下含边裂纹功能梯度条二维模型,梯度条沿着x方向为无限长,并且该材料的热机械属性仅随y方向变化.如图1所示,功能梯度条的厚度为h,T1、T2分别为梯度条上下表面的温度,T0为无应力状态时的初始温度.
为了求解热应力定义如下参数:弹性模量E、泊松比ν、密度ρ、热膨胀系数a、热传导率k和比热容c.
1.1 求解温度场
一维瞬态热传导方程为
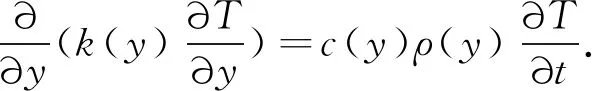
(1)
式中:ρ(y)、k(y)和c(y)分别是y方向任意位置的密度、热导率和比热容;T表示温度场;t为时间.初始条件和边界条件为
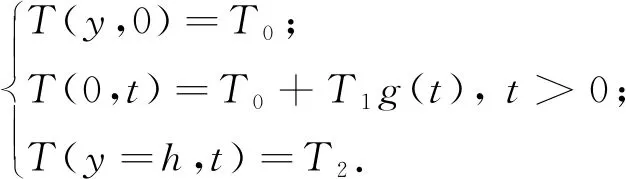
(2)
如图1(b)所示为3种升温函数(无量纲)与时间(无量纲)的关系,其中指数升温方程[12-13]f(t)表示为
f(t)=1-exp(-υtt),
(3)
线性升温方程[12,14]f(t)表示为
f(t)=-υ′tt.
(4)
υt,υ′t分别是指数升温和线性升温的升温速率系数.假设
υ′t=(1-e-vtτm)/τm.
(5)
式中τm是温度升高到T1所需要的时间.
考虑一维情况下的准静态问题,可以在直角坐标系中将经受平面应变变形的非均质固体的热弹性方程写为
(6)
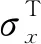
得出式(6)的通解为
式中A和B为积分常数,可由以下平衡方程得到

(8)
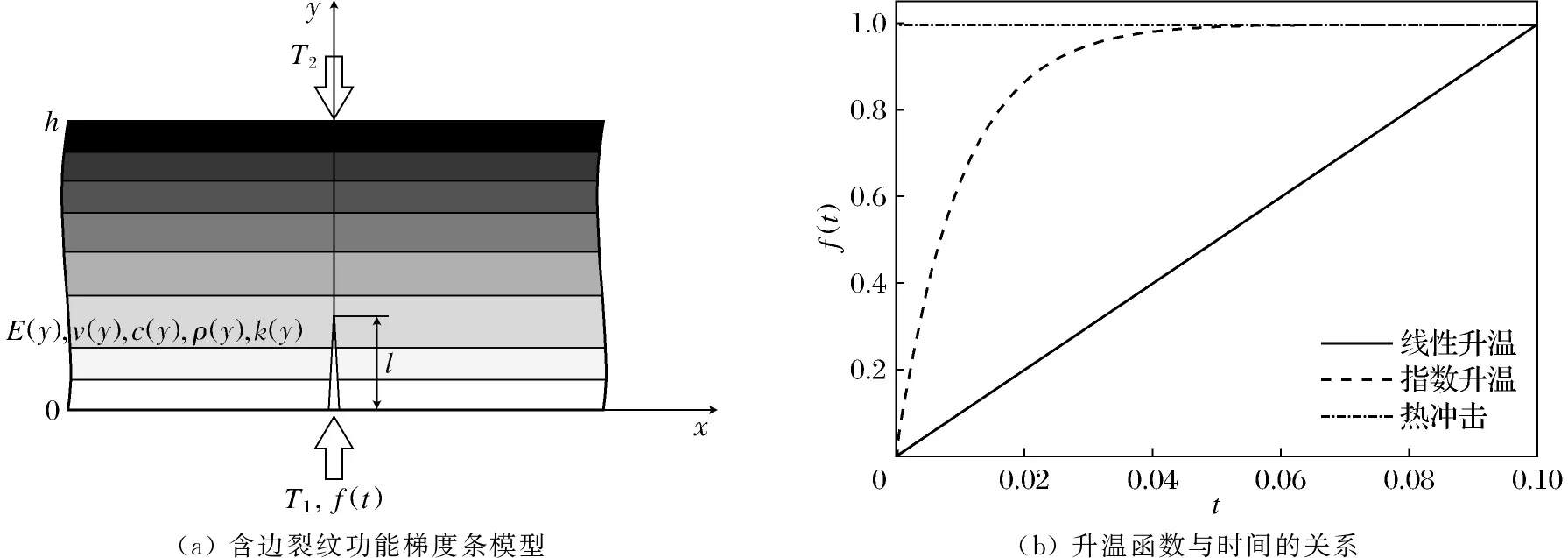
(a) 含边裂纹功能梯度条模型(b) 升温函数与时间的关系
图1热载荷作用下含边裂纹功能梯度条二维模型
Fig.1Two-dimensionalmodeloffunctionalgradientstripwithedgecracksunderthermalload
1.2 求解热应力
本文采用分层思想将功能梯度条沿着y方向分成N个均匀层,并将每一段看作为均质材料,并且认为材料各属性参量均为常数,因此,各单层的温度场满足微分方程
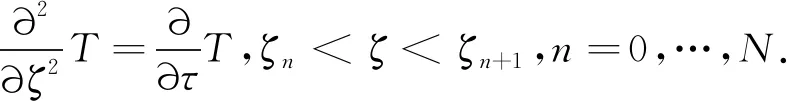
(9)
为了推导方便,定义以下无量纲参数:
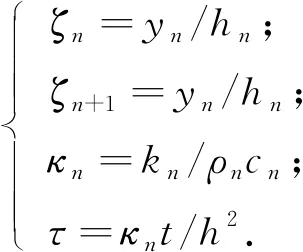
(10)
式中:ζ是一个已知的任意实函数;ζn和ζn+1分别表示第n层的上下表面y轴坐标;κn、kn、cn和ρn为第n层的热扩散率、热导率、比热容以及密度;τ为时间.
因此,可得第n层上下表面温度场可表示为
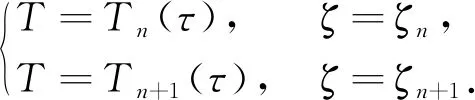
(11)
层间界面处的温度场连续性条件可表示为
(12)
结合式(2)~式(4)中的初始条件,利用分离变量法和拉普拉斯变换对式(10)进行求解[10].
式中F1(τ)=Tn(τ),F2(τ)=Tn+1(τ),此外,本文由于篇幅原因部分参数未提及.
根据文献[10],将温度函数式(13)代入式(7)得热应力方程
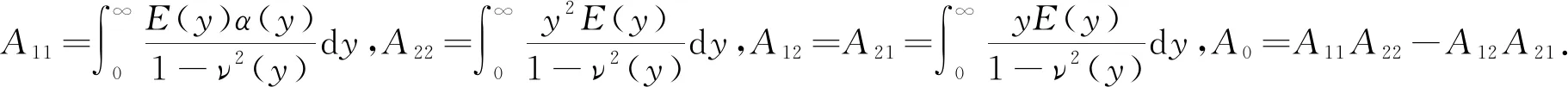
1.3 求解裂纹强度因子
该裂纹问题可用叠加原理求解,即首先求解热传导问题并获得热应力,其次,将不含裂纹情况下的热应力问题转化成等温下裂纹表面含有与热应力等值反向的载荷问题.通过叠加就可以将该问题转化为求解裂纹表面载荷的问题.
该问题的边界条件和连续性条件为
u(ζ)=0,ζ∉(0,l/h).
(15)
为了求解积分,定义辅助函数ω(ζ),
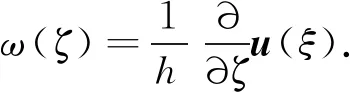
(16)
则式(15)可化成
式中u(ζ)为沿x方向的位移矢量,l为裂纹长度.
应用文献[15]中使用的数值方法求解边裂纹的奇异积分方程组,其表达式为
该未知的φ(s,τ)可表示为[16]
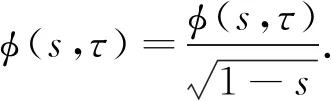
(22)
其中,φ(s,τ)表示不存在奇异性的函数.
最终可求得裂纹尖端处的无量纲热应力强度因子表达式如下:
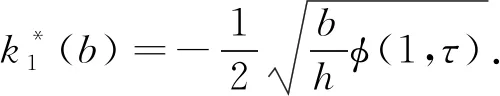
(23)
2 算例与结果分析
为验证模型的有效性,本文选取由TiC和Ni 2种典型材料组成的两相功能梯度材料体系进行研究(TiC和Ni功能材料的物理性能参数见表1),该材料具有抗热冲击,防止应力在界面处集中等特点[17-18].层数N是20.本文采用文献[4]中的指数函数对材料的热机械属性进行表征,其表达式为:
X(y)=Xceln(Xm/Xc)(y/h)
(24)
其中:X(y)为FGM材料的热机械属性函数,X可分别为弹性模量E、泊松比ν、热膨胀系数a、热导率k、密度ρ以及质量定压热容C等物理量,m和c分别为代表金属相和陶瓷相的下角标,此外,当y=0时,表示为纯基体相,当y=h时,表示为纯夹杂相.

表1 TiC和Ni功能材料的物理性能参数Table 1 Physical performance parameters of TiC and Ni functional materials
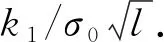
σ0=αcEcT1/(1-νc).
2.1 不同升温条件下的热应力分布
下面考虑在不同升温条件下,功能梯度条的上下表面温度比率为(T1/T2=30)的热应力分布情况.
图2给出了T1/T2=30条件下,不同升温条件下最大热拉应力σ(无量纲)在功能梯度条不同位置处的变化情况.从图2可以看出,升温速率的不同会导致最大拉应力的幅值、产生时间以及在材料中发生位置的差异性.这说明随着升温速率的增加将会导致最大拉应力的增大,同时也会将应力峰值移向升温表面.
图3所示分别为3种升温条件下材料表面及中心位置的热应力(无量纲)分布随时间(无量纲)的变化曲线.图中可见当时间较短时,3种情况下的平板表面都受压应力, 而中心位置则都受拉应力. 然而, 随着时间的增加, 3种升温速率下的材料表面及中心位置热应力呈现出不同的变化趋势: 在指数升温和热冲击情况下, 材料的中心位置及下表面受到的热应力会达到一个峰值, 然后缓慢降低,而在线性升温情况下, 热应力呈现单调增加的趋势; 相对于热冲击加载而言, 虽然材料上表面在指数升温加载时受到的压应力在温度加载初期(τ≤0.02)时在绝对值上呈现了上升的趋势, 但是随着时间的增加, 其热压应力绝对值趋于减小, 此外, 材料上表面在线性升温速率下受到的热压应力同样保持增加的趋势.
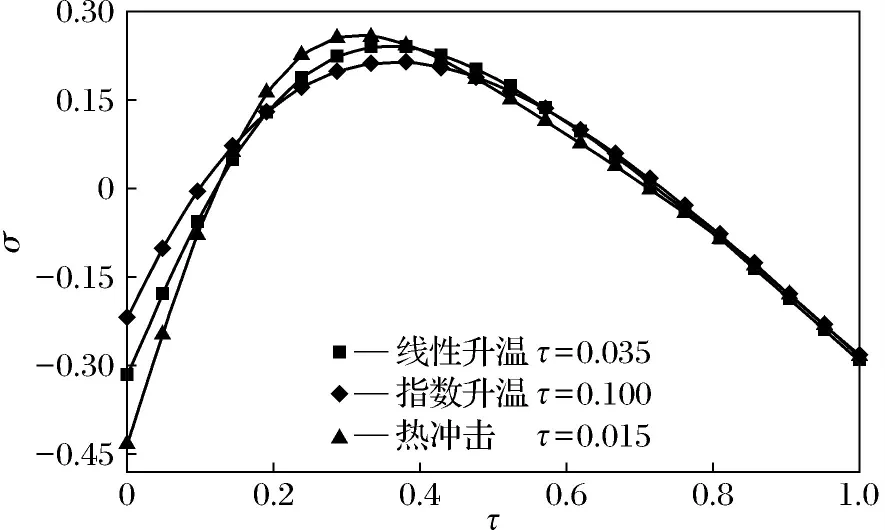
图2不同升温条件下最大热拉应力随时间的变化曲线
Fig.2Curvesofmaximumthermaltensilestresswithtimeunderdifferentheatingconditions

(a) 线性升温(b) 热冲击(c) 指数升温
图3不同升温条件下梯度材料不同位置的热应力随时间的变化曲线
Fig.3Curvesofthermalstresswithtimefordifferentpositionsofgradientmaterialsunderdifferenttemperaturerisingconditions
2.2 裂纹长度变化下的热应力强度因子
为了分析不同升温速率对材料小裂纹的热应力强度因子的影响情况,本文考虑Ⅰ型裂纹问题,为了简化裂纹分析的计算,本文考虑了一种特殊的FGM,其中认为FGM材料的泊松比和弹性模量均为常数[5],对于杨氏模量变化不大的材料(例如氧化锆/钢,氧化锆/镍体系),这种假设也很有用.
由于在本文中不考虑表面裂纹接触问题,因此应力强度因子在进入受压区域后出现负值.当裂纹长度l≤临界裂纹长度a0时,热应力强度因子在压应力区域.在不同的升温条件下,裂纹长度临界值不同,其压应力区域范围也不同.表2所示为3种升温条件下升温结束时的裂纹长度临界值.从表中可以看出,随着升温速率的增加,压应力区域的范围逐渐减小.本文中我们考虑了初始裂纹长度为a0≤l≤0.15h的情况.

表2 不同升温条件下临界裂纹长度Table 2 Critical crack length under different heat rate
图4给出了裂纹长度l分别在0.05、0.10和0.15h的条件下,裂纹尖端处的热应力强度因子TSIF(无量纲)在不同升温条件下随时间的变化情况.

(a) l=0.05h(b) l=0.10h(c) l=0.15h
图4不同升温条件下含边裂纹功能梯度TSIF随时间的变化曲线
Fig.4CurvesofTSIFgradientwithedgecrackswithtimeunderdifferentheatingconditions
由图4可知,试样的应力强度因子随裂纹长度增加而增大.此外,随着升温速度的增加,应力场在裂纹尖端处也会随之增加,而材料受到的热应力也会更早的变化,这说明随着升温速率的增加会导致热压应力区域的减小.同样,在热冲击作用下,裂缝面效应的重叠最大化并且是最短暂的.而对于线性升温情况下,很明显观察到,当裂纹长度大于等于0.15h时,试样加热结束后发现TSIF略有增加,而对于长度小于0.15h的裂纹,其试样的应力强度因子随时间变化较为平缓,说明在当前裂纹情况下保持了较好的稳定性.
3 结 论
研究了含裂纹的非均质功能梯度条在受到热冲击,指数升温和线性升温情况下的热应力和应力强度因子的影响.结果表明:
1) 升温速率的降低将会导致功能梯度条受到的热应力减少;
2) 功能梯度条在热冲击和指数升温情况下受到的最大热应力差异显著;
3) 材料中受到的拉、压应力在线性升温情况下将会同时增加;
4) 升温速率的降低以及边裂纹长度的减小将会导致材料中裂纹稳定性增加;
5) 升温速率的降低导致FGM裂纹扩展开始延迟.

