MATLAB程序设计在导数教学中的应用

陈佳佳 孔新海 李义林

摘要：根据导数的定义及几何意义，基于MATLAB软件平台，通过图形静态演示、动态演示、数据驗证三步骤进行导数教学设计，帮助高职工科类学生理解导数基本定义、概念及定理，激发学生学习高等数学兴趣。利用MATLAB中的动画设计方法把抽象的数学定义直观展示出来，提升教学效果，在高职工科类专业高等数学教学中有一定的应用价值。

关键词：高等数学;MATLAB软件;导数;分段函数

中图分类号：TP311;G642    文献标识码：A    文章编号：1007-9416（2020）04-0000-00

0 引言

高等数学中的基本概念多且抽象，对于高职工科类专业学生来讲，难以理解。传统教学方式是教师在黑板上作图，但这种作图方式较为粗糙，缺乏准确性，且不具有迁移性。所以探索有效的教学方法和教学手段，将数学知识生动形象地展示出来，激发学生的学习兴趣，使得其轻松掌握知识点，是高等数学教学中亟需解决的问题。下面以导数教学为例，利用MATLAB软件平台，通过图形静态演示、动态演示、数据验证等步骤来讲授导数概念。

1 导数教学设计思路

导数是高等数学微分学中的基本概念，它是由极限来定义的。由于极限本身描述的是一个过程，高职工科类专业的学生很难从文字上理解导数的相关知识。若能借助MATLAB中的动画设计方法，结合导数的几何意义，将整个教学过程动态化，能大大提升教学效果。由此我们首先利用MATLAB程序设计[1-3]，选择几个点，定性、静态地描述时割线位置的变化情况，帮助学生理解导数的几何意义。再利用极限的思想，选取较小的步长，采用动画设计，动态演示当时割线的位置变化情况，结合导数存在的判定定理得出结论。最后，结合定义，利用程序验证前面得出来的结论。

正弦函数在工科类专业中运用广泛，这里以函数在（0，0）处的导数为例。因为当，在处分段。对于分段函数，要描述其在分段点的导数情况，要求出函数在分段点的左导数与右导数，再运用相应的判定定理，则可得到相应的结论。

2 MATLAB静态子图演示设计

首先讨论当，在处的右导数。根据MATLAB中的函数“diff”，利用点斜式，画出函数曲线在处右边的切线。根据导数的几何意义[4]，是曲线上邻近的一点，依次取为，，，，做割线，利用MATLAB中子图呈现的方式，画出这四条割线的静态子图（如图1）。由图1可以直观看出当时割线是逐渐靠近切线。由于子图显示的个数有限，我们只选了步长为0.5的四个点的割线来做参考，若能选择更小的步长，呈现当时割线移动的动态过程，则更能体现导数的定义。

3 MATLAB动态辅助教学系统演示设计

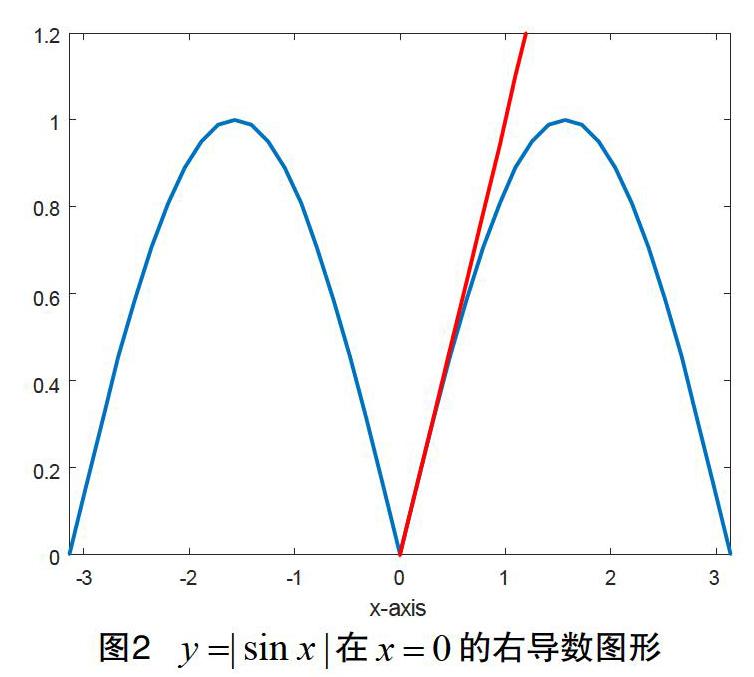
下面我们利用程序动画方式，结合极限的定义，步长设置为0.05，演示当时，在处的右导数（见图2）。其部分核心代码如下：

for  m=0：0.05：Maxdx

plot（x，y，'linewidth'，1.5）

hold on

x1=x0+（Maxdx-m）;         %从右边趋于0（即）

y1=f1（x1）;

k=（y1-y0）/（x1-x0）;

fge=@（x）y0+k*（x-x0）;      %利用点斜式求函数在处右边切线

yge=fge（x）;

plot（x，yge，'r'，'linewidth'，1.5）

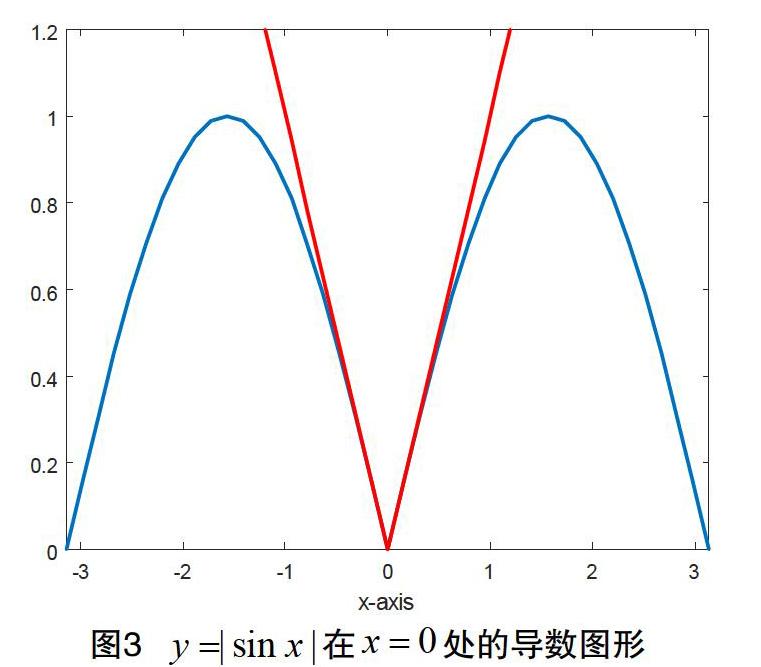
if m

pause（0.5）

hold off

else

hold on

end

end

同理讨论当时，在的左导数图形，其核心代码区别在x1=x0-（Maxdx-m）;学生观测到在处的有两条切线且不重合（见图3）。

根据导数的唯一性，即得出分段函数在分段点处的导数不存在，学生因此更容易理解知识点。

4 利用MATLAB进行数据验证

从定义出发，利用MATLAB程序语言，编制计算程序，核心代码如下：

x=-2*pi：pi/20：2*pi;

y=abs（sin（x））;

syms x

syms d positive

f_R=sin（x）;

df_R=limit（（subs（f_R，x，x+d）-f_R）/d，d，0）

df_R0=limit（（subs（f_R，x，d）-subs（f_R，x，0））/d，d，0）  %在分段点处的右导数

f_L=-sin（x）;

df_L=limit（（f_L-subs（f_L，x，x-d））/d，d，0）

df_L0=limit（（subs（f_L，x，0）-subs（f_L，x，-d））/d，d，0）  %在分段点处的左导数

命令运行结果：df_R0 =1，df_L0 =-1。由此可知在分段点处的左导数和右导数存在但不相等，所以根据定理可知，在分段点处不可导，验证了由图形得出的结论。

5 结语

通过程序代码控制，更精确地展现了数形之间的关系，对高等数学抽象概念的演示效果更好。在我校工科类专业的教学效果调查中，同学们都认为使用演示软件后知识点更容易理解，对于高等数学的认识不再停留于只有数字和概念了，大大提升了学习效果和学习兴趣。

参考文献

[1]刘建军，武国宁，陳小民.基于Matlab的高等数学实验式教学演示设计[J].内蒙古师范大学学报（教育科学版），2016，29（4）：130-132.

[2]刘兵.基于MATLAB GUI的导数辅助教学演示系统的开发[J].实验科学与技术，2018，16（5）：81-84.

[3]秦立春.利用matlab辅助两个重要极限教学的课堂设计[J].教育教学论坛，2014（19）：97-98.

[4]赵勇，李义林.高等数学[M].哈尔滨工业大学出版社，2019.

收稿日期：2020-03-14

基金项目：中国职业技术教育学会教学工作委员会2019-2020年度职业教育教学改革课题“新时代背景下高职院校工科类专业《高等数学》课程改革与实施”，编号：1910095。

作者简介：陈佳佳（1986—），女，四川邻水人，硕士，研究方向：数学教育。

Application of MATLAB Programming in the Derivative Teaching

CHEN Jia-jia， KONG Xin-hai， LI Yi-lin

（Guang'an Vocational and Technical College， Guang'an Sichuan  638000）

Abstract： According to the definition and geometric meaning of the derivative， based on the MATLAB software platform， through three steps of graphic static demonstration， dynamic demonstration， and data verification， the instructional design of the derivative is designed to help the students of the senior staff to understand the basic definition， concept and theorem of the derivative， and motivate the students interesting to learn Higher mathematics . Using the animation design method in MATLAB to display the abstract mathematical definitions intuitively and improve the teaching effect， it has a certain application value in the Higher mathematics teaching.

Key words： Higher mathemsatics; MATLAB software; derivative; piecewise function