新型偏心啮合盘元件的混沌混合特性

沈美震，任建民，朱向哲，李万旭

(1.辽宁石油化工大学机械工程学院，辽宁抚顺 113001； 2.中国石油天然气第八建设有限公司，辽宁抚顺 113006)

啮合同向双螺杆挤出机作为聚合物混合和加工的主要设备之一，一直以来都凭借其良好的混合特性和灵活简便的结构而被广泛应用[1–2]。聚合物加工行业的发展对传统双螺杆挤出机提出了更为严苛的要求，为了满足产业需求，研究者需要在已有的基础上进行理论创新和构型改造。

混沌混合理论是提高熔体混合效率的重要理论基础之一[3]。诱发混沌混合有多重途径，其主要有往复搅拌、变速搅拌和偏心搅拌等。偏心搅拌主要是对流道内的空间配置进行布局，具体则是针对螺棱形状、大小和位置，螺棱与转子根部到旋转轴心距离的比值等，其直接目的便是使搅拌更加无序化，以便加快混沌混合这一过程[4]。M. M. Alvarez 等[5–6]研究了层流流动下偏心搅拌的混合性能，指出偏心距的改变显著影响层流流场。G. Ascanio 等[7]也对层流流动下偏心搅拌的混合性能进行了研究，指出在搅拌较高黏度流体时，偏心搅拌无论是对轴向混合能力还是周向混合能力都有较好的提升。

混沌混合较传统的分散和分布混合机理有较大不同，但两者又相辅相成。混沌混合的实质为反复的拉伸和折叠[8]。混沌混合中拉伸的过程即产生拉伸流的过程，拉伸流有利于分散相的破裂从而提高分散混合能力[9]。转子啮合区剪切速率较大，此处存在双曲不动点，由于流体粒子运动空间有限，高剪切使其产生较为明显的折叠效果，从而增强了混沌混合[10]。修正的李雅普诺夫指数是用来表示聚合物熔体在混合停留时间内的平均拉伸应变率，直接描述了双转子连续混合机在混合过程中混沌混合行为和所经历的分布混合强度和大小，其指数值越大，拉伸应变越大，分布混合能力越强，各组分在共混物中的均匀性和分散性越好，分散相组分在连续相中的分布越均匀[11]。总的来说，转子具有较高的剪切和拉伸能力可以增强混沌混合的强度，而具有较高的周向和轴向混合能力则可以从侧面反映出其具有较大体积的混沌混合区域。

基于上述理论对比了偏心圆啮合盘元件与传统双头啮合盘元件后发现，偏心圆啮合盘元件具有较好的混沌混合效果。笔者旨在对新型偏心圆啮合盘元件的流动特点和混合效果进行分析，并通过改变错列角和偏心距，得出这两种几何参数对偏心圆啮合盘元件混合特点与混合效率的影响。同时还比较了三种典型粒子的运动轨迹和混合特性参数，为深入了解偏心搅拌提供了理论支持。

1 物理模型

1．1 几何模型与网格划分

偏心圆啮合盘造型较为简单，生产工艺要求和造价较低，灵活多变的组合方式更易于与其它啮合元件组成规格和功能不同的捏合区域。偏心圆啮合盘元件左右相互交错啮合的盘片形成较大面积的轴向间隙和周向间隙，左右两啮合盘所形成的轴向间隙大小不随转动角度变化而变化，位置则随转动角度呈周期性左右摆动。由于两转子同向旋转，左右啮合盘所形成的轴向间隙和周向间隙内相对运动明显，为其提供了较多的高剪切区域。

表1 为螺杆和机筒的几何尺寸，相对应的机筒尺寸见图1a。笔者主要对比了偏心圆啮合盘元件不同的错列角和偏心距这两个几何参数，设置了以下5 组对照模型：错列角为30°，偏心距为4.5 mm；错列角为60°，偏心距为4.5 mm；错列角为90°，偏心距为4.5 mm；错列角为90°，偏心距为5 mm；错列角为90°，偏心距为6 mm。

表1 螺杆和机筒几何尺寸特征 mm

偏心圆啮合盘元件转动见图1b。可以看出，两机筒流域的周向截面形似两个半月形圆弧，左右两啮合盘元件顺时针转动，在转子的挤压下使得半月形的流动空间左移，熔体因挤压作用沿机筒顺时针转动。在左端螺棱运动到两机筒交界处的端点时，两机筒所夹区域形成周向较封闭区域且该区域体积在不断减小，熔体由于挤压作用快速向前输运，形成短时间的挤压窜流，转子转动的每个周期会出现两次。由于挤出机对熔体具有输送能力，所以熔体同时向前平稳输送。

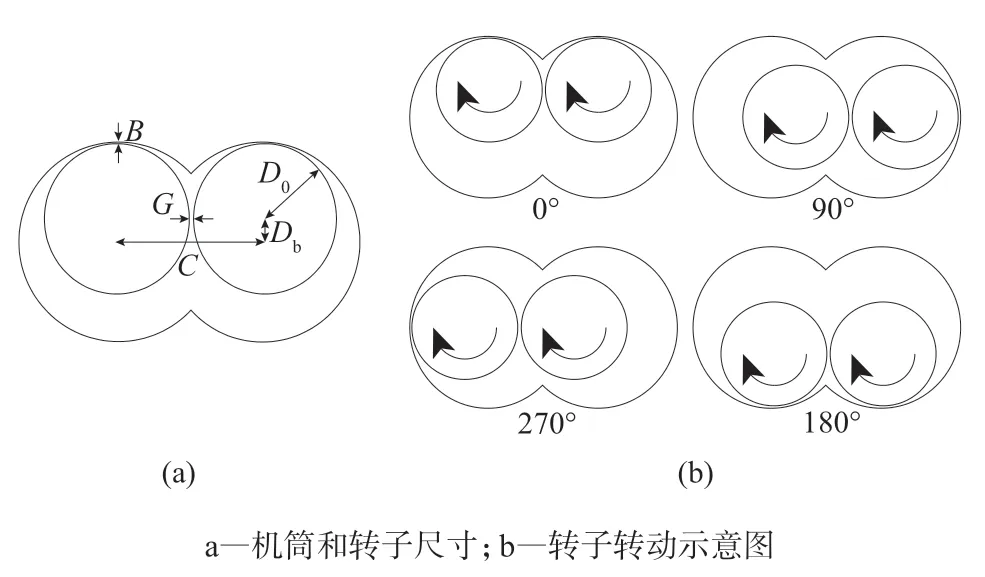
图1 机筒和转子尺寸及转动示意图

机筒采用结构网格划分为数量437 230 的网格，转子采用结构网格划分数量为57 613。由于机筒边界处和啮合盘捏合区流体流动变化较明显，故在此处采用边界层网格加密，如图2 所示。

图2 有限元模型

1．2 数学模型

流道内流体流动十分复杂，为了方便计算，忽略影响较小的因素，并假设：①流体为幂律流体；②流体为层流不可压缩流体；③流场为等温稳定流场；④忽略惯性力和体积力；⑤流道内壁面和螺杆壁面无滑移；⑥物料完全充满。

基于以上假设和网格叠加技术(MST)，并在直角坐标系下建立方程。

连续方程：

动量方程：

式中：∇为哈密顿算子；v为速度矢量；T为切应力张量；P为压力。

本构方程：

式中：η∝为剪切速率无穷大下的黏度数值；η0为零剪切黏度；λ为松弛时间；γ为剪切速率；n为幂律指数。

平均对数线拉伸率：

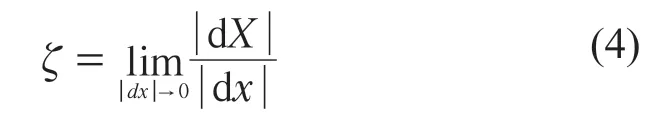
式中：ζ为平均对数线拉伸率；x为粒子初始时刻的位置；X为粒子在t时刻的位置；dx为流体平均对数拉伸微元，且dx=F·dX(F 为变形梯度张量)。

粒子分布指数：

式中：ε为粒子分布指数；Freal(l)，Fopt(l)为概率函数；l为粒子间距。

粒子分布指数是用来评价粒子随时间的混合效果。假设初始时刻有N颗粒子集中在一定空间内，粒子之间对流场无影响，也不相互影响。在t时刻有N颗粒子组成N(N–1)／2 组粒子对。每组粒子对的位置分别为Xi和Xj，其最短距离dij= |Xi–Xj|，最大距离为流道的最大直径。粒子对相互之间的距离小于l的概率为Freal(l)。当粒子均匀分布在流道内时的粒子间距作为最优分布，粒子对之间相互距离小于l的概率密度函数为Fopt(l)。其中当粒子束分布指数减小时，表明混合效果提高。

为了提高计算精度，选择收敛慢且相对稳定的Picard 迭代，速度场采用mini-element，压力则利用线性关系求解，瞬态流场分析采用Galerkin 积分法。

1．3 边界条件

为了使模型封闭计算收敛有解，假设边界条件为：机筒内表面速度为0；流域入口流量3.1×10–6m3；流域出口压力 3×106Pa；左右转子同向旋转转速相同，为150 r／min。

2 网格无关性验证

在实际操作中网格的稀疏和稠密直接影响计算结果的精度，理论上网格密度越高计算精度越高，但是现实中计算机的运算能力是有限的，在运算能力允许的范围内使得计算结果尽量精确是研究者努力去实现的目标。

图3 是螺杆在检测线上的速度值，其分别将流域划分为周向30 层、40 层和60 层的网格。从图3可以看出，检测线上的速度值相差很小，故可以推断网格密度对结果精确度影响较小，即网格无关性成立。以下采用周向网格数量为40 层的网格作为模型进行分析。

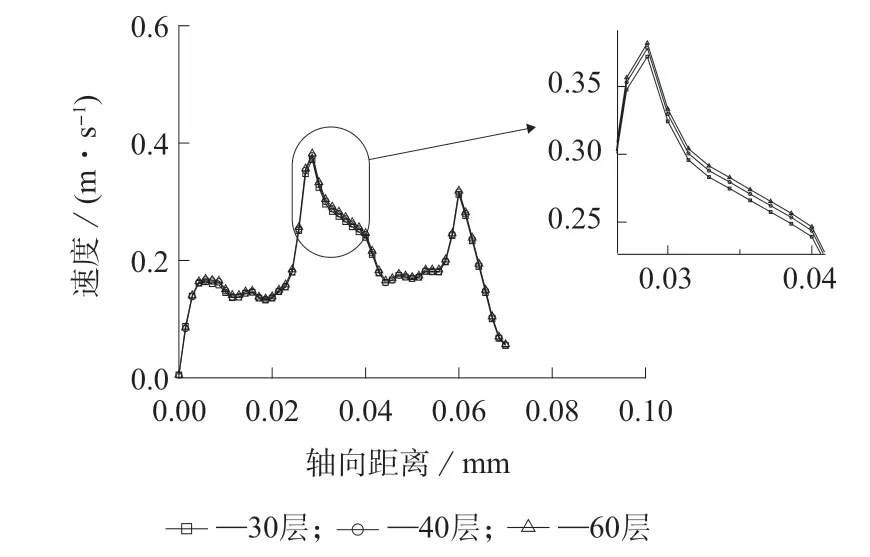
图3 不同网格密度时偏心圆啮合盘元件在检测线上的速度值

3 结果与讨论

3．1 流动特性分析

(1)压力场分析。

图4 给出了初始时刻机筒内表面和沿轴的机筒中心截面的压力场分布。从图4a 可以看到，偏心圆啮合盘元件的机筒内表面压力沿挤出方向有所上升，熔体在机筒前半段压力值则较为平稳，而机筒后段压力急剧升高，这是由于偏心圆啮合盘元件错开的啮合盘对于熔体的流动产生了屏障作用，阻碍了熔体的流动，其形成的轴向压差有利于物料沿轴向的回流，提高了轴向混合能力[12]。从图4b可以看到，螺棱两侧的推力面和拖拽面使得运动前后区域形成压力梯度[13]，这是由于偏心圆啮合盘元件较为宽大的螺棱使得转子与机筒之间有较大面积的螺棱顶隙，从而产生了较强的挤压作用。由图4b 还可以看出偏心圆啮合盘元件较常规啮合盘元件具有较高的左右转子区周向压力差，这有利于熔体从压力高的一侧沿压力梯度流向压力低的一侧，形成压力窜流，从而提高周向混合能力。

图4 压力分布云图

(2)速度矢量场分析。

图5 是偏心圆啮合盘元件初始时刻宏观速度矢量图，图中矢量箭头长短代表速度大小，箭头长度越长代表速度越大；矢量箭头方向越广数量越密集，则说明物料在流道中的流动性越好。图5a 中箭头长度较长的三处区域是流动性相对较好的区域，其主要出现在两螺棱中间的位置如图5b 所示，其形成原因主要是由于左右转子相互挤压熔体致使熔体向前快速流动所造成的。由于偏心圆啮合盘元件较为平滑的螺棱表面并未对机筒产生刮壁现象，所以螺棱顶隙处并未出现高流动区域。

(3)剪切速度场分析。

图6 给出了初始时刻机筒内表面和周向截面的剪切速率分布。从图6 可看出，高剪切速率区域主要出现在偏心圆啮合盘元件的螺棱顶隙处和左右两转子所形成的轴向间隙处，这是由于螺棱两侧的推力面和拖拽面使得运动前后区域形成的压力梯度，使得熔体沿压力梯度由高压区流向低压区增加了流动性，且螺棱顶隙与轴向间隙处转子相对运动明显，速度梯度较大，从而产生了较高的剪切速率区域。

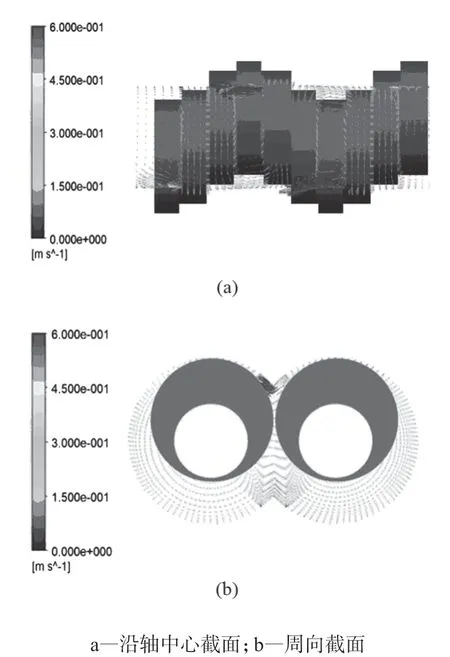
图5 速度矢量图

图6 剪切速率分布云图

(4)混合指数。

混合指数是用来表征混合特性的一种评价参数，其值范围是0～1。当混合指数接近0 时，流体主要以漩涡流的形式存在；当混合指数接近0.5 时，流体主要以剪切流的形式存在；当混合指数接近1时，流体主要以拉伸流的形式存在。图7 为初始时刻两种典型旋转位置下的混合指数云图。从图7 可以看出，以旋涡流为主的区域主要出现在背螺棱一侧的内侧，其流动性相对较差，其主要原因是此区域受到偏心圆啮合盘元件错开的啮合盘的屏障作用，阻碍了熔体的流动，并且此处无螺棱的扰动，速度梯度较小，导致此处流动性较差。图7 中以剪切流为主的区域主要出现在螺棱顶隙与轴向间隙处，在前面剪切速度场分析中已经得出此结论，除此之外，以剪切流为主的区域还出现在机筒和转子壁面处，这是因为在拉伸流靠近壁面的位置由于壁面粘滞力的作用使得拉伸流逐渐过渡为剪切流。图7 中以拉伸流为主的区域主要出现在背螺棱一侧的外侧，其流动性较好，这是由于周向压力差的存在使得流体沿压力梯度流动，从而产生了较强的拉伸流，拉伸流对分散混合的能力提升明显。

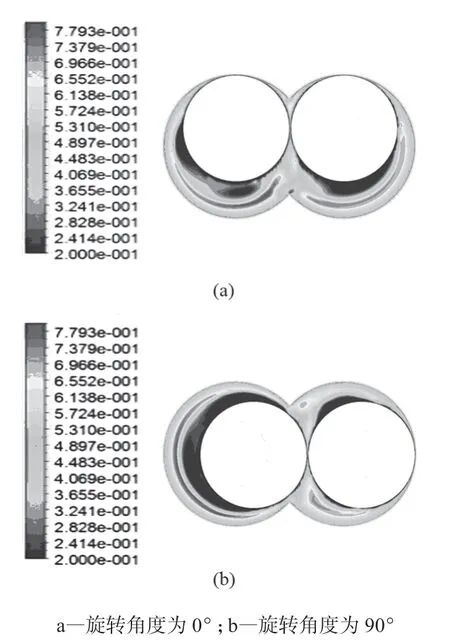
图7 两种典型旋转位置下周向截面的混合指数云图

3．2 混合效率分析

(1)对数线拉伸指数。

J. M. H. Janssen[9]进一步完善了液滴破碎机理，指出液滴在力的作用下被拉长，当伸长到一定程度时发生破裂形成较小液滴，这种情况下拉伸流较剪切流更有助于减小液滴半径，从而提高分散混合的能力。图8 为不同几何参数对数拉伸率对比。

图8a 中，错列角为60°的偏心圆啮合盘元件的对数拉伸率在运动到1.5 s 以后逐渐高于30°和90°的偏心圆啮合盘元件，由此推断出错列角为60°的偏心圆啮合盘元件拉伸混合能力更佳。图8b 中，偏心距为5 mm 的偏心圆啮合盘元件的对数拉伸率在运动到2.5 s 以后逐渐高于4.5 mm 和6 mm 的偏心圆啮合盘元件，由此推断出偏心距为5 mm 的偏心圆啮合盘元件拉伸混合能力更佳。

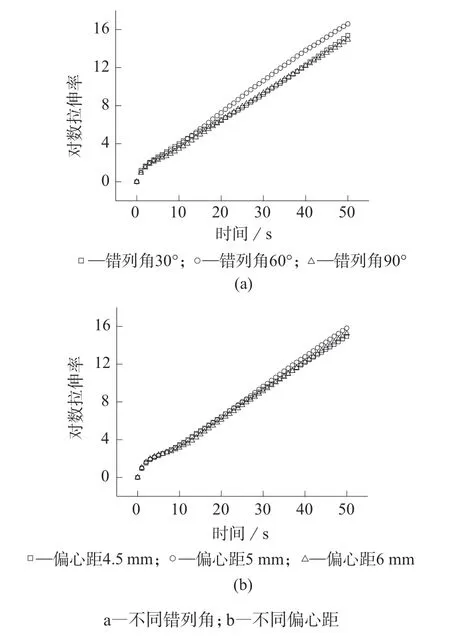
图8 不同几何参数的对数拉伸率对比

(2)累积最大剪切速率。

图9 为不同几何参数最大剪切速率对比。图中某一点横坐标为a，纵坐标为b，则说明有b%的粒子经历的最大剪切速率小于a，曲线排列越靠右侧则剪切能力越强[14]。图9a 中，错列角为60°的偏心圆啮合盘元件所在曲线要明显靠近右侧，并且在剪切速率达到5 000 s–1后，此优势更加明显，所以错列角为60°的偏心圆啮合盘元件具有更高的剪切混合能力。图9b 中偏心距为5 mm 的偏心圆啮合盘元件所在曲线更靠近右侧，并且在剪切速率达到3 000 s–1后，此优势更加明显，所以偏心距为5 mm的偏心圆啮合盘元件具有更高的剪切混合能力。

(3)停留时间分布。

停留时间是衡量物料分布混合的的重要参数之一[15]。停留时间密度分布曲线越靠近右侧则表明停留时间越长分布混合越好，曲线分布越宽则表明轴向混合能力越强，轴向混合越均匀。图10a 中，错列角为60°的偏心圆啮合盘元件所在曲线更靠右侧，形状更宽，所以验证了60°的偏心圆啮合盘元件具有较好的轴向混合能力。图10b 中，偏心距为5 mm 的偏心圆啮合盘元件所在曲线更靠近右侧，所以偏心距为5 mm 的偏心圆啮合盘元件具有较好的轴向混合能力。

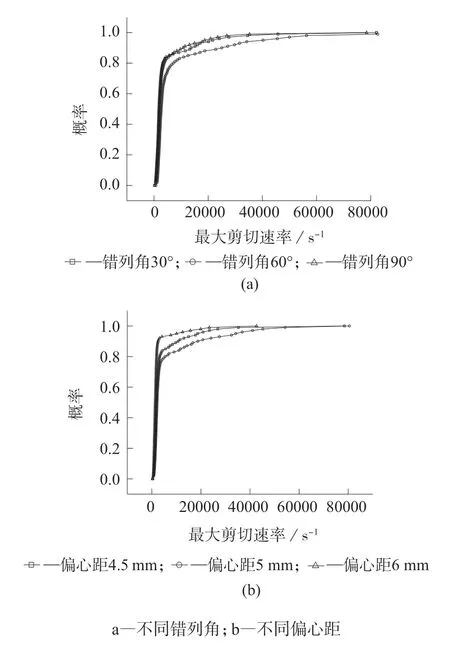
图9 不同几何参数最大剪切速率对比

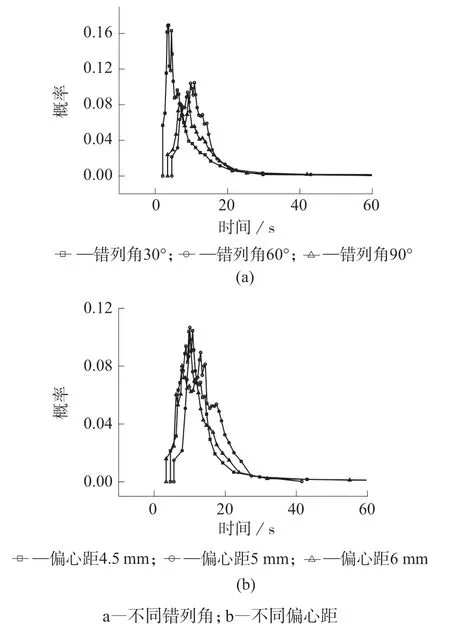
图10 不同几何参数停留时间分布对比

(4)分布指数和分离尺度。

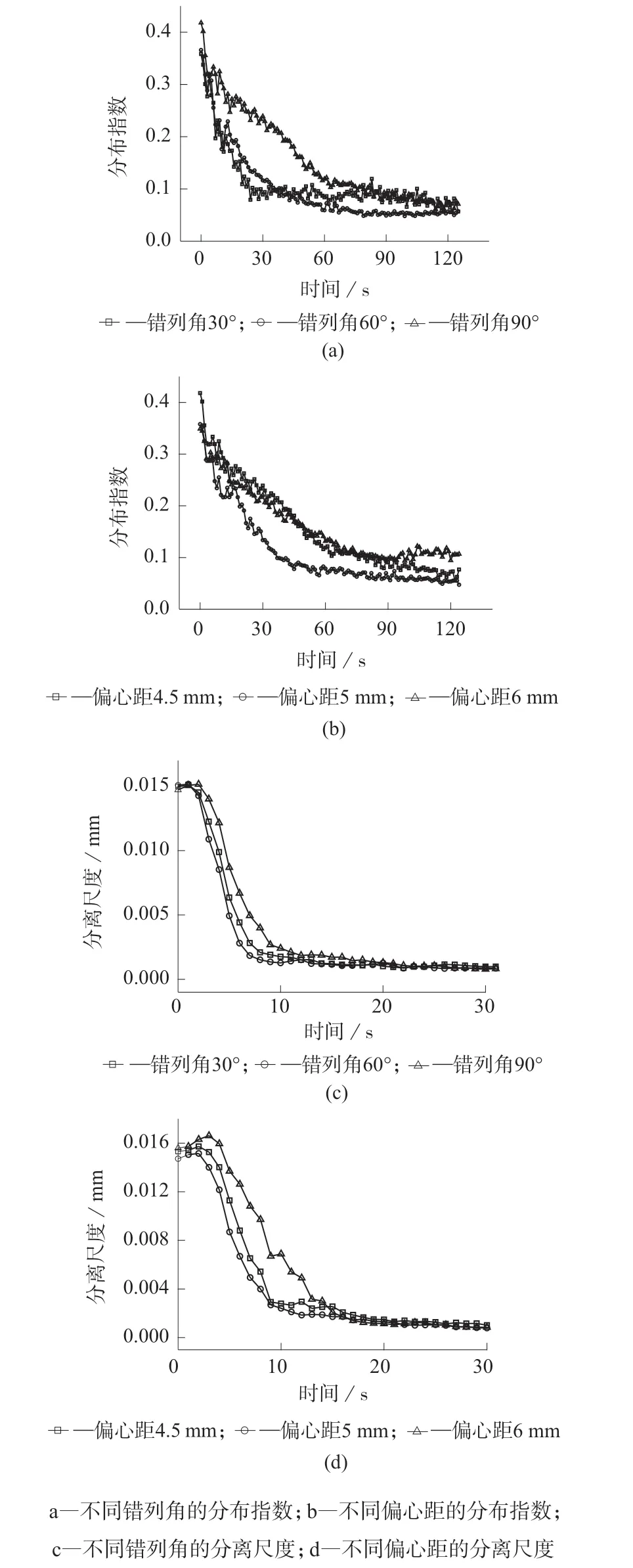
图11 不同几何参数分布指数和分离尺度对比

分布指数是用来衡量分布混合能力的重要指标，示踪粒子与最优分布之间的差异越小则证明分布混合能力越佳[16]。图11 为不同几何参数分布指数和分离尺度对比。从图11a 以看出，两条曲线在初始时刻分离尺度均处于一个较高的位置，这是因为示踪粒子初始时刻都积聚在机筒入口端面的左右两侧，所以开始时分离尺度处于高位。两条曲线的初始分离尺度不同是由于回流使得进入到流域内的粒子数量不同所造成的。接下来随着混合的进行，错列角为60°的偏心圆啮合盘元件分布指数逐渐低于错列角为30°和90°的偏心圆啮合盘元件。这说明错列角为60°的偏心圆啮合盘元件拥有较好的分布混合能力。如图11b 所示，偏心距为5 mm的偏心圆啮合盘元件所在曲线明显低于4.5 mm和6 mm 的偏心圆啮合盘元件，这说明偏心距为5 mm 的偏心圆啮合盘元件分布混合能力更佳。

分离尺度表示混合物中相同组分区域平均尺寸的度量，其数值随着分散混合程度的提高而减小[17]。图中曲线可以看出偏心圆啮合盘元件其平缓的螺棱表面未能对熔体产生汇流作用，所以线形较为均匀并未出现较大波动，并且其较好的剪切作用和拉伸作用使得两种示踪粒子平稳高效地混合在一起。由图11c 可看出，错列角60°的偏心圆啮合盘元件所在曲线明显低于30°和90°的偏心圆啮合盘元件所在曲线，所以错列角为60°的偏心圆啮合盘元件拥有较好的分散混合能力。由图11d 可看出，偏心距5 mm 的偏心圆啮合盘元件所在曲线较偏心距为4.5 mm 和6 mm 的偏心圆啮合盘元件所在曲线低，所以偏心距5 mm 的偏心圆啮合盘元件分散混合能力更佳。

(5)粒子可视化及单个粒子混合特性。

假设流道入口均匀释放2 000 个示踪粒子，对粒子在50 s 内的运动进行了跟踪。图12 为典型的单个粒子运动轨迹，图中小点为每单位时间步长下的坐标位置，粒子的运动轨迹便是由这许多的点组成。通过对粒子的运动轨迹观察发现，机筒中一部分粒子沿机筒内壁做圆环型移动，如图12a 所示，由于受到机筒内壁粘滞力的作用粒子运动相对平稳缓慢，且未进入到左右转子之间啮合区。还有一部分粒子运动较为活跃，如图12b 所示，其粒子的两位移位置坐标点相隔较远，运动速度较大，绕转子旋转圈数较多，且多次进入左右转子啮合区。还有极少数粒子在螺杆根部区域滞留时间较长，如图12c 所示，螺杆根部区域熔体流动性较差造成了极少数示踪粒子滞留在此区域。

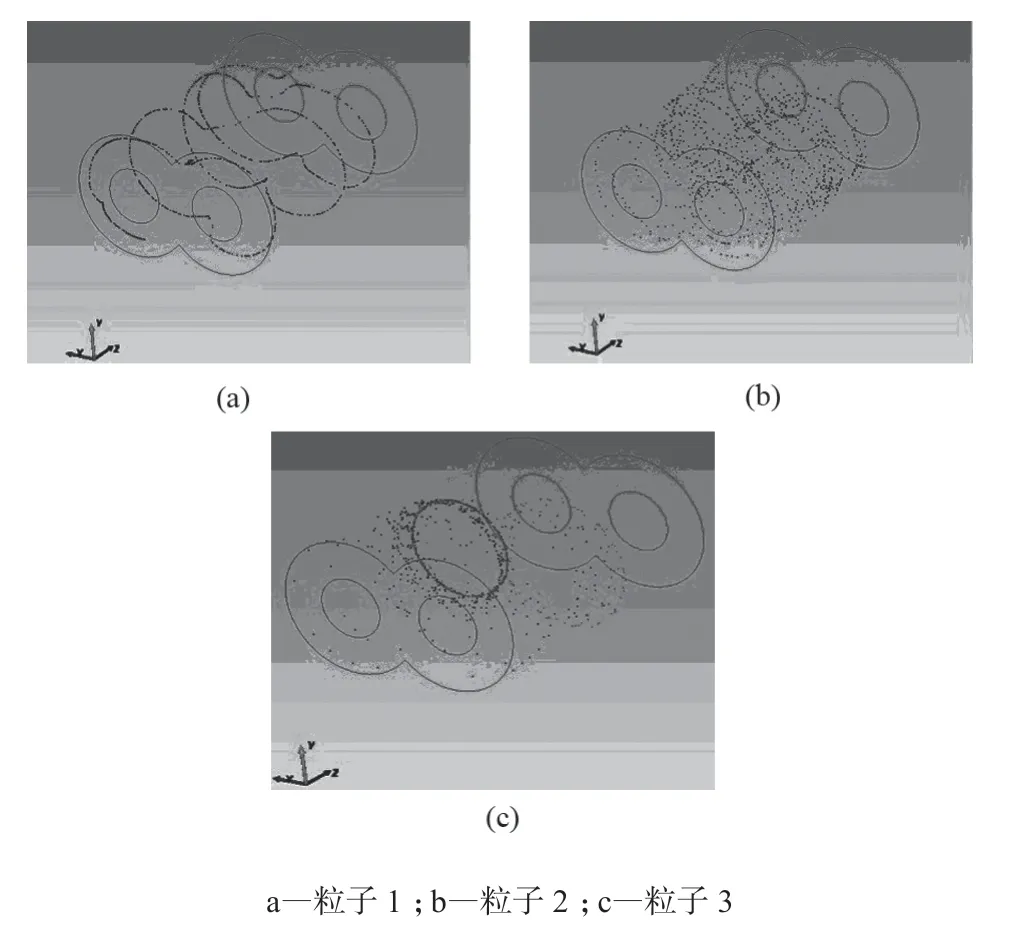
图12 示踪粒子运动轨迹

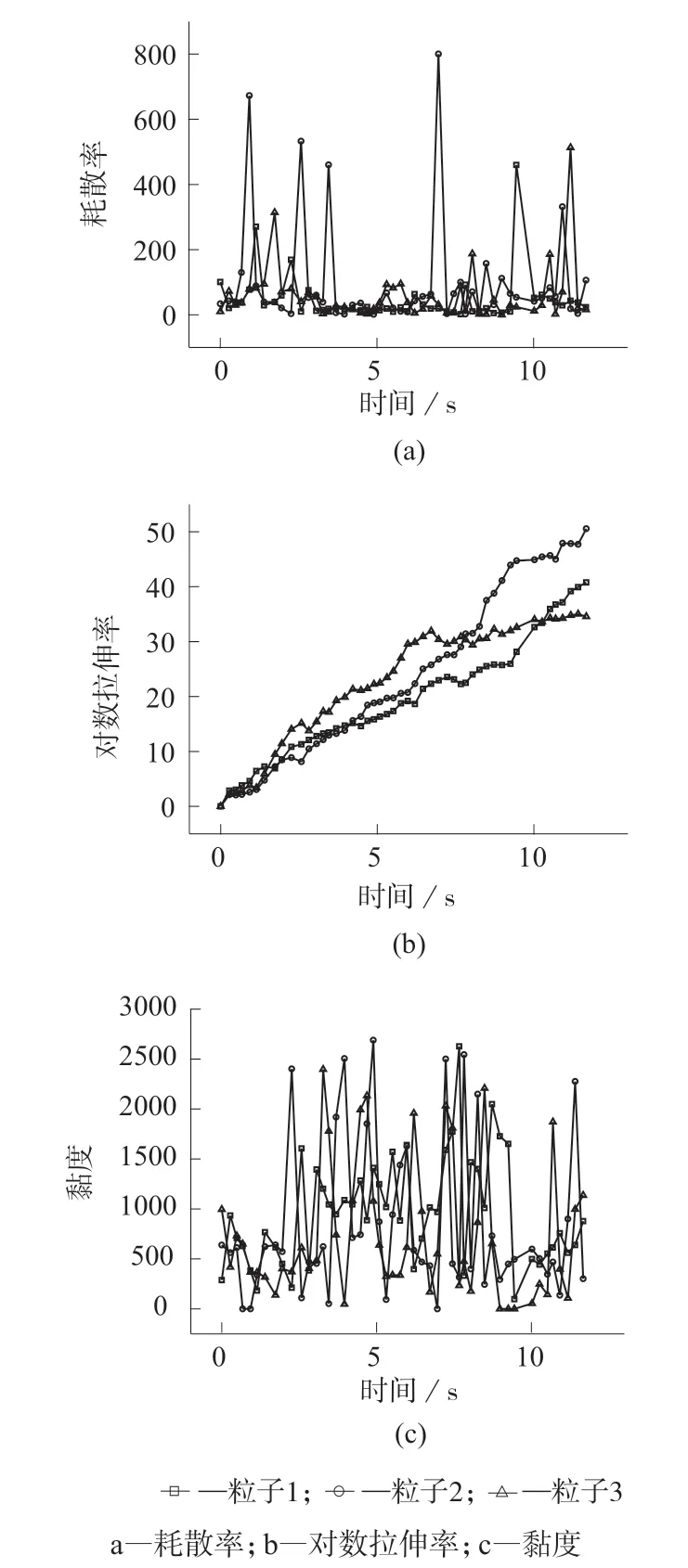
图13 单个粒子混合特性曲线

图13 为上述三种粒子的混合特性曲线。通过对典型粒子耗散率、对数拉伸率、黏度的突变规律分析，可以更加深入地了解双螺杆挤出机中熔体的流动和混合机理。粒子1 的总体流动性较差，其耗散率相对较低，由于贴近壁面故其拉伸指数也相对较低，但由于螺棱顶隙的存在使得沿机筒前进的粒子也具有相对稳定且较好的剪切速率，所以其剪切黏度也较为平稳。粒子2 总体一直处于流动性较好的状态，所以其耗散率和对数拉伸率都处于相对高的数值，由于其多次经历左右两转子所夹高剪切啮合区域，剪切变稀使其黏度值波动相对较大。粒子3前段流动性相对较好，所以其耗散率和对数拉伸率数值相对较高，而到了中段粒子运动逐渐拐入螺棱根部造成物料滞留，所以耗散率和对数拉伸率逐渐下降，由于左右两螺棱周向间隙的存在，使螺棱根部的粒子也能经受较高的剪切，所以其剪切黏度波动相对较高。

4 结论

(1)偏心圆啮合盘元件在轴向和周向都具有较大的压力梯度，物料沿压力梯度流动，提高了轴向和周向混合效率。偏心圆啮合盘元件较为平滑的螺棱表面未对机筒内熔体产生较大扰动，只在两螺棱之间区域存在较短时间的高流动区域。偏心圆啮合盘元件宽大的螺棱使其具有较大面积的螺棱顶隙，再加上较大面积的左右转子相互啮合所形成的轴向间隙和周向间隙，这些都为其提供了较高的剪切混合区域，从而提高了其剪切混合能力。偏心圆啮合盘元件由于较强的周向和轴向压力梯度，从而产生较强的拉伸流，增强了混沌混合效果，提高了分散混合能力。

(2)错列角为60°和偏心距为5 mm 的偏心圆啮合盘元件更利于推动和拖拽熔体沿运动方向流动，实现熔体的多向流动，产生较强的压力窜流，从而促进了物料的轴向混合和周向混合，提高了其分布混合效率。该组合偏心圆啮合盘元件还具有较好的拉伸流动和剪切流动，从而提高了分散混合效率。

(3)由单个粒子轨迹及其混合特性曲线可知，粒子流经机筒内壁和螺棱根部之间区域时混合效果较为理想，粒子运动靠近机筒则剪切和拉伸下降明显，而靠近螺棱根部粒子流动迟缓，发生粒子滞留现象。