基于可信性的模块化软件开发费用分配算法*
马艳芳,王梦月,周 伟,陈 亮
(1.淮北师范大学计算机科学与技术学院,安徽 淮北 235000;2.淮北师范大学数学科学学院,安徽 淮北 235000)
1 引言
在网络技术快速发展的时代,软件在人们的生活中扮演着重要角色[1]。软件系统广泛地应用到各行各业中,尤其是交通、军事、金融等重要领域[2]。然而,软件系统的失效和故障给人们的生活带来很多不利影响,有时甚至会威胁到生命安全。由此,软件质量问题受到了人们的高度关注。软件可信性作为衡量软件质量的重要指标,在软件工程中占有重要的地位。
软件可信性是20世纪90年代引入软件工程领域的新概念,最早是由Laprie[3]提出并与软件可靠性作区分。目前,国内外专家在软件可信性的定义方面尚未达成共识。美国国家研究委员会给出了一个与软件可信性有关的定义[4]。他们认为即使在环境发生崩溃、操作人员出现操作失误等情况下,一个系统也能按照预期的方式运行,则该系统是可信的。国家自然科学基金委员会于2007年批准立项了“可信软件基础研究”重大研究计划[1]。该项目委员会认为可信软件是指系统的动态行为及其结果总是符合人们的预期,并在受到干扰时仍能提供连续服务的软件。“可信”是在传统的安全、可靠等概念基础上发展起来的一个相对较新的学术概念。王怀民等[5]对可信软件的概念作了进一步补充,他们认为如果一个软件系统的行为总是和用户的预期相符合,则称软件是可信的,并把软件的可信性定义为软件按照用户预期提供安全可靠服务的能力。陶红伟[6]从最终用户的角度出发,认为软件可信性是软件的行为和结果符合用户预期,并在受到干扰时仍能提供连续服务的能力。由此可见,人们虽然对软件可信性的理解不同,但是都认为软件可信性可以反映软件质量的好坏,可以作为衡量软件质量的重要标准。
目前,国内外学者已经在软件可信性方面取得很多研究成果。软件可信性度量与评估是对软件的可信性进行量化评价,通过量化评估可以为增加软件研发的可信性提供依据[6]。王婧等[7]提出了一套面向航天型号软件的可信性度量模型以及分级评价方法,并已成功地运用于航天型号软件的可信性评估。郎波等[8]提出了软件可信分级模型,能够对软件的可信性划分等级,为软件可信评估机制提供理论依据与方法。软件可信性可以通过一系列的属性来刻画。为了确定属性的权重,张俊等[9]在保证各属性重要度的基础上,结合属性之间的相互影响程度,建立了属性权重分配模型。陶红伟[6]将属性分为关键属性和非关键属性,建立了基于属性的软件可信性度量模型。随着“软件过程也是软件”的提出,王德鑫等[10]从过程的实体、行为以及制品方面提取软件可信的证据,提出了软件过程可信度量模型。随着组件化软件开发方法的发展,Mubarak等[11]提出了一种严格的以组件为中心的可信软件系统开发的新过程模型。Huang等[12]基于组件之间不同的连接方式建立了软件可信性度量模型。Wang等[2]提出了一种基于组件的可信度更新模型,该模型根据用户的反馈计算组件的可信程度,更新的权重由用户数量决定。软件可信属性可分为功能属性和非功能属性,用户对非功能属性的满足程度直接影响软件质量的好坏[1]。由此,罗新星等[13]提出了一种基于关键非功能属性的软件可信性度量模型。张璇等[14]基于利益相关者对非功能属性的优先级约束和基线约束,提出了非功能属性权衡代价分析方法,该方法可以帮助利益相关者选择最优策略。而为了保证软件的可信性,软件需求分析人员需要确定软件中各个单元的可信性需求,由此软件的可信性分配问题成为需要解决的问题[15]。楼俊钢等[16]为了对可信性属性进行量化分配,在三角模糊数和层次分析法的基础上,提出了一种模糊层次分析法。Ma等[15]建立了基于属性的可信性分配模型及其可信分配算法,并已应用于嵌入式航天软件中,足以证明其有效性且对软件可信性的研究有指导作用。在文献[6]的基础上,Tao等[17]进一步提出了基于子属性的软件可信性分配模型。黄杜娟[18]在保证达到用户给定的软件系统可信性目标的情况下,研究如何分配构成系统各个子系统的可信性指标,使得软件所需开发费用最小。
近年来,软件系统的结构越来越复杂,模块化开发方法已成为开发软件产品的主要发展趋势之一。作为软件的使用者,用户在安装系统的时候可以根据个人的需求选择模块。由此可见,模块化软件的可信性研究非常重要。Alexopoulos等[19]提出了一个基于模块化软件的完整软件系统可信度评估模型。但是,随着软件系统越来越庞大,开发软件系统的费用与日剧增。在实际生活中,软件系统必须是在用户给定的开发费用内开发完成,而在研究模块化软件的可信性时上述模型却忽视了软件开发费用。因此,在用户给定的开发费用内如何合理分配各模块的开发费用,使得软件系统可信性达到最优,是一个很有意义的研究课题。
2 模块化软件
软件系统体系结构是系统的全局视图和主要结构。研究其层次设计时,依据研究的范围将体系结构整体分解为多个组成部分。文献[20]给出了软件体系结构的层次框架图,如图1所示。

Figure 1 Hierarchical framework of software architecture图1 软件体系结构的层次框架图
软件体系结构自上而下逐层分解直至模块。模块是功能完整、可重用的对象,通常只关注模块外的功能和交互特征,不需要了解模块的内部结构。每个模块既可以单独使用,也可以进行组合使用。模块化软件由多个功能独立的模块组成,模块之间的相互作用形成软件系统的所有功能。模块通过顺序、分支、并行和循环的方式连接,进而构成软件系统。
3 模块的可信性费用预估模型
提高模块的可信性需花费一定的费用,只有确定了模块的可信性与费用的关系才能在用户给定的开发费用内得到系统最优可信性。因此,确定模块的可信性与费用之间的关系是首要任务。
一方面,可靠性是属于可信性的一个重要属性,研究可信性的同时也在研究可靠性;另一方面,提高模块可信性的费用很大程度上花费在提高可靠性上,由此,根据可靠性与费用之间的关系,建立模块的可信性费用预估模型[1]。因此,借鉴文献[21]中的可靠性与费用之间的关系,下面给出模块可信性费用预估函数的定义:
定义1假设T∈(0,1)是模块的可信性,f∈(0,1)是模块的复杂度,D是模块开发的初始成本,令:
(1)
则称C(T)是模块的可信性费用预估函数。
由式(1)可知,模块结构简单,开发难度小,其所需开发费用低;相反,模块结构复杂,开发难度大,其所需开发费用相对较高;当模块的可信性越接近于最大可信性时,开发费用会迅速增加到无穷大。
式(1)满足1986年Dale等[22]提出的费用函数性质,模块的可信性费用预估函数性质如下所示:
性质1假设一个软件系统由n个模块组成,第i(1≤i≤n)个模块的可信性为Ti,记C(T′i)-C(Ti)表示将模块的可信性从Ti提高到T′i所需要的费用,0 (1)提高模块可信性的费用是非负的,即C(T′i)-C(Ti)≥0; (3)当0 证明 (3)计算可得C(T′i)-C(Ti)+C(T″i)-C(T′i) =C(T″i)-C(Ti)。 □ 假设一个软件系统由n个模块M1,M2,…,Mn组成,每个模块在进行组装之前已初步开发完成,具有一定的可信性。软件工程师对各模块可信性进行评估,此阶段评估值可作为各模块的初始可信性,令模块Mi的初始可信性为Ti.min,其中1≤i≤n,0 开发人员会首先根据所需模块的可信性指标制定各个模块的开发计划。因此,如果开发人员决定开发某个模块时,才会投入资源制定开发计划,提高模块的可信性直到最大可信性;而若对某个模块的可信性要求不高,则不需要浪费资源制定开发计划,保证模块的初始可信性即可。因此,利用0-1背包问题的思想,令一个n元0/1数组x=[x1,x2,…,xi,…,xn]表示各个模块的开发情况,xi=1表示分配开发费用Wi开发模块Mi并达到其最大可信性Ti.max;xi=0表示没有分配开发费用给模块Mi,此时模块Mi的可信性为初始可信性Ti.min。 各模块根据不同的组合方式构成一个复杂的软件系统,而软件系统的可信性由各模块可信性及其组成方式所决定。由此,令g表示各模块之间的不同组成方式的函数,模块的可信性分别为T1,T2,…,Tn,得目标函数和约束条件为: T=maxg(T1,T2,…,Tn) (2) 其中,Ti是模块Mi的可信性,当xi=0时,Ti=Ti.min;当xi=1时,Ti=Ti.max。Wi是提高模块Mi到最大可信性的所需费用;W为软件开发费用。根据最优解x=[x1,x2,…,xn],将模块可信性代入式(2),即得到软件系统的最优可信性。 在顺序结构中,每个模块相互独立,依次执行[12],如图2所示。软件系统中一个模块的错误将导致系统出错,即模块的可信性越低,系统的可信性越低。因此,采用连乘各模块可信性的方法求解系统的最优可信性。 Figure 2 Software system with sequence structure图2 顺序结构的软件系统 得目标函数和约束条件为: (3) 根据最优解x=[x1,x2,…,xn],将模块可信性代入式(3),即得到软件系统的最优可信性。 根据模块的个数和用户给定的开发费用进行子问题的划分。设Fi(y)max表示存在并只开发前i个模块,开发费用y不超过W时系统的最大可信性,分2种情况考虑: (1)不开发第i个模块,那么只能开发前(i-1)个模块,此时开发费用仍为y,则系统的最大可信性是Fi-1(y)max; (2)使用开发费用Wi开发了第i个模块,此时剩下的开发费用(y-Wi)用于开发前(i-1)个模块。 由此,得到顺序结构下的软件可信性与费用分配问题的递推关系: Fi(y)max=max{Fi-1(y)max· Ti.min,Fi-1(y-Wi)max·Ti.max} F0(y)max=1,0≤y≤W Fi(y)max=-∞,y<0 其中,F0(y)max是不开发任何一个模块的系统可信性,理论上F0(y)max=0。因为顺序结构下的软件系统可信性是连乘所有模块的可信性得到的,在递推过程中,当i=1时,F1(y)max=max{F0(y)max·T1.min,F0(y-W1)max·T1.max},为了使F0(y)max·T1.min≠0,F0(y-W1)max·T1.max≠0,令F0(y)max=1(0≤y≤W)。当软件系统只由一个模块组成时,若y 算法1顺序结构下的软件可信性与费用分配算法 Input:n,W,w[n]={W1,…,Wn},r[n]={T1.min,…,Tn.min},t[n]={T1.max,…,Tn.max}。 Output:最优解x[n],最大可信性V[n][W]。 1.forj←1toWdo 2.V[0][j]←0; 3.fori←1tondo 4.forj←1toWdo 5.ifj 6.V[i][j]←V[i-1][j]*r[i]; 7.elseV[i][j]←max(V[i-1][j]*r[i],V[i-1][j-w[i]]*t[i]); 8.endif 9.endfor 10.endfor 11.j←W; 12.fori←nto1 step -1do 13.ifV[i][j]/r[i]>V[i-1][j]then 14.x[i]←1;j←j-w[i]; 15.elsex[i]←0; 16.endif 17.endfor 18.returnx[n],V[n][W] 算法分析:时间效率为O(nW)。空间效率为用于存储二维数组的空间大小,即为O(nW)。 在分支结构中,每次运行时,系统会以一定的概率选择其中的一个分支来运行[12],而概率信息代表每个模块的运行次数,如图3所示。 Figure 3 Software system with branch structure图3 分支结构的软件系统 得目标函数和约束条件为: (4) 根据模块的个数和用户给定的开发费用进行子问题的划分,划分方法与4.2节的顺序结构下的划分方法相同。由此,得到分支结构下的软件可信性与费用分配问题的递推关系: Fi(y)max=max{Fi-1(y)max+piTi.min, Fi-1(y-Wi)max+piTi.max} F0(y)max=0,0≤y≤W Fi(y)max=-∞,y<0 其中,F0(y)max是不开发任何一个模块的系统最大可信性,即F0(y)max=0。当软件系统只由一个模块组成时,若y 算法2分支结构下的软件可信性与费用分配算法 Input:n,W,w[n]={W1,…,Wn},r[n]={T1.min,…,Tn.min},t[n]={T1.max,…,Tn.max}。 Output:最优解x[n],最大可信性V[n][W]。 1.forj←1toWdo 2.V[0][j]←0; 3.fori←1tondo 4.forj←1toWdo 5.ifj 6.V[i][j]←V[i-1][j]+pi*r[i]; 7.elseV[i][j]←max(V[i-1][j]+pi*r[i],V[i-1][j-w[i]]+pi*t[i]); 8.endif 9.endfor 10.endfor 11.j←W; 12.fori←nto1 step -1do 13.ifV[i][j]-pi*r[i]>V[i-1][j]then 14.x[i]←1;j←j-w[i]; 15.elsex[i]←0; 16.endif 17.endfor 18.returnx[n],V[n][W] 算法分析:时间效率为O(nW)。空间效率为用于存储二维数组的空间大小,即为O(nW)。 在并行结构中,存在2种基本情况。第1种是与并行,只有当所有模块都运行成功时,整个系统才是成功的。与并行结构下的软件可信性与费用分配模型同4.2节的顺序结构下的模型相同。第2种是或并行,只要有一个模块运行成功即可[12],如图4所示。 Figure 4 Software system with or parallel structure图4 或并行结构的软件系统 得目标函数和约束条件为: (5) 根据最优解x=[x1,x2,…,xn],将模块可信性代入式(5),即可得到软件系统的最优可信性。 由此,得到或并行结构下的软件可信性与费用分配问题的递推关系: Fi(y)min=min{Fi-1(y)min·(1-Ti.min), Fi-1(y-Wi)min·(1-Ti.max)} F0(y)min=1,0≤y≤W Fi(y)min=-∞,y<0 算法3或并行结构下的软件可信性与费用分配算法 Input:n,W,w[n]={W1,…,Wn},r[n]={T1.min,…,Tn.min},t[n]={T1.max,…,Tn.max}。 Output:最优解x[n],最小可信性M[n][W]。 1.forj←1toWdo 2.M[0][j]←0; 3.fori←1tondo 4.forj←1toWdo 5.ifj 6.M[i][j]←M[i-1][j]*(1-r[i]); 7.elseM[i][j]←min(M[i-1][j]*(1-r[i]),M[i-1][j-w[i]]*(1-t[i])); 8.endif 9.endfor 10.endfor 11.j←W; 12.fori←nto1 step -1do 13.ifM[i][j]/(1-r[i]) 14.x[i]←1;j←j-w[i]; 15.elsex[i]←0; 16.endif 17.endfor 18.returnx[n],M[n][W] 算法分析:时间效率为O(nW)。空间效率为用于存储二维数组的空间大小,即为O(nW)。 软件系统中的一个或多个模块被重复执行时就构成了一个循环体[12]。假设循环体为A,循环次数是t,如图5所示。 Figure 5 Software system with loop structure图5 循环结构的软件系统 循环体A是由模块M1,M2,…,Mn组成,模块之间的组合方式可能是顺序、分支或并行。利用式(3)~式(5)可得到循环体A的可信性。令TA表示循环体的可信性,若循环体A为顺序结构,则TA=TS;若循环体A为分支结构,则TA=TB;若循环体A为并行结构,则TA=TP。假设循环次数为t,且t≥1,得目标函数和约束条件为: (6) 根据最优解x=[x1,x2,…,xn],将模块可信性代入式(6),即得到软件系统的最优可信性。 目前,基于软件可信性讨论开发费用分配的研究尚少,大部分研究聚焦于软件可信性的分配方法。然而,在软件开发过程中,提高软件系统的可信性需要花费巨大的成本,所以在软件开发过程中,考虑软件开发费用的分配具有十分重要的意义。 (1)文献[15]在基于用户给定的软件系统可信性目标的基础上,建立了软件属性的可信性分配模型,具体如下所示: 其中,yi=y*+k(αi-αmin)是第i个属性的可信性;y*是第i个属性必须满足的最低可信性;αi是第i个属性的权重;αmin是最小权重;k是属性的可信增长率,所有属性的可信增长率相同;T*是用户给定的软件系统必须满足的可信性目标。 步骤1令属性集合N={1,2,…,n},M>1=∅。 步骤3将可信增长率k代入式yi=y*+k(αi-αmin),i∈N-M>1,求得各个属性的可信性。如果yi>1,则重新赋值yi=1,并将第i个属性放入集合M>1,M>1=M>1∪{i}。 重复步骤2~步驟3,直到所有属性的可信性小于或等于1,即属性的可信性分配结束。 然而,该模型只考虑了属性的可信性分配,并未考虑软件开发费用的分配问题。 (2)文献[2]提出了一种基于用户反馈的软件可信性更新模型,具体如下所示: 其中,Tn是更新后的软件可信性;Tu是用户反馈的可信性;T0是软件原始的可信性;ω0是软件原始的可信性权重;n是用户个数;ωu(n)是用户反馈的权重。 该模型根据用户的反馈和用户数量重新分配属性的权重,计算更新后的软件可信性,然而,该模型也并未考虑软件开发费用分配这个重要的问题。 (3)文献[18]是在满足用户给定的软件可信性目标的前提下,研究如何分配各个子系统的可信性,使得软件所需开发费用最小,提出的模型如下所示: s.t.f(Ti)≥Tobj 其中,E是软件系统的开发费用,Ei是第i个子系统的开发费用,f表示各子系统之间的组成方式,Ti是第i个子系统的可信性,Tobj是用户给定的软件系统的可信性目标。然而,在实际软件开发过程中,软件系统是在给定的开发费用内开发完成的。 软件开发费用是研究软件开发必须优先考虑的重要因素。在用户给定的软件开发费用内如何实现软件系统的可信性最优化具有重要的研究意义,然而,当前关于这一方面尚无更好的研究成果。 Figure 6 Automatic ticketing system图6 自动售票系统 假设用户给定的软件开发费用为70,各模块初始开发费用为5。模块的复杂度fi、初始可信性Ti,min、最大可信性Ti,max及达到最大可信性Wi所需的费用如表1所示。 Table 1 Complexity,initial trustworthiness,maximum trustworthiness and corresponding cost表1 复杂度、初始可信性、最大可信性及达到最大可信性所需的费用 可得模块M1和M2组成的登录功能的初始可信性为0.96,最大可信性为0.99,所需花费为20。同理可得,模块M3和M4组成的订票功能的初始可信性为0.64,最大可信性为0.92,所需花费为25。模块M1和M2组成或并行结构后,再与模块M3和M4组成的分支结构顺序连接,最后依次再与模块M5,M6,M7顺序连接构成,则整个系统的结构可看作是顺序结构,利用式(2)可得目标函数为:TS=max[1-(1-T1)(1-T2)]·[(p3T3+p4T4)]2·T5·T6·T7。 由算法1可得,最优解为x=[0,1,1,1,0],即分别分配开发费用0,0,15,10,20,25,0给模块M1,M2,M3,M4,M5,M6和M7,则T1=0.8,T2=0.8,T3=0.99,T4=0.9,T5=0.99,T6=0.99,T7=0.9,可得TS=0.78,即软件系统的最优可信性为0.78。 软件开发费用分配是软件可信性工程中的重要环节。首先建立模块的可信性费用预估模型。其次,根据软件系统的不同结构特点,建立顺序、并行、分支和循环结构下的软件可信性与费用分配模型和分配算法。在给定的软件开发费用内,利用动态规划进行费用分配,使得软件系统的可信性最优。该模型不仅可以运用于简单系统,也可以运用于大型复杂系统。如何确定模型的参数,则是需要进一步深入探讨的问题。同时,在今后的工作中,还需要通过实际项目中的应用来进一步检验该模型的有效性和可操作性。






4 软件可信性与费用分配模型
4.1 软件可信性与费用分配问题描述
4.2 顺序结构下的软件可信性与费用分配模型
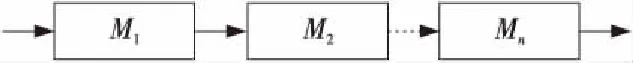
4.3 分支结构下的软件可信性与费用分配模型


4.4 并行结构下的软件可信性与费用分配模型



4.5 循环结构下的软件可信性与费用分配模型



5 算例分析



6 结束语

