全变分正则化非局部均值地震数据降噪*

李晓璐,周亚同,何静飞,翁丽源,李书华

(1.河北工业大学电子信息工程学院，天津 300401;2.天津市区第三烟草专卖局,天津 300131 )

1 引言

地震数据降噪对地下结构分析及资源采集有重要意义[1,2]。常见的降噪算法可分为变换域降噪和空域降噪2个类型。

常见的变换域降噪算法有小波变换[3]、曲波变换[4]以及从小波变换发展起来的高斯混合模型[5]等。在空间域常用的降噪算法有均值滤波[6]、中值滤波[7]和高斯滤波[5]等。Buades等[8]提出了非局部均值算法，以小邻域为单元进行加权运算，利用冗余信息在有效保持结构的同时进行噪声压制。黄英等[9]用像素值的相似性来代替像素点的空间距离，Chang等[10]使用高斯模型代替非局部均值算法中使用全部相似数据块的加权平均，实现了对随机噪声的压制。

尽管非局部均值算法在降噪方面表现良好,但有可能会选入一些并不相关的邻域，造成噪声斑块抖动效应，边缘细节被过度平滑。针对这一缺点，本文结合空间域和偏微分方程降噪算法对地震数据进行降噪。

偏微分方程降噪可以很好地保持边缘细节，它将降噪转化为偏微分方程求解，且地震数据具有可微分性，全变分降噪算法不仅能够消除地震噪声，而且可以大面积提高剖面质量。本文基于Sutour等[11]的工作并结合全变分模型可以有效保护边缘细节的特点，提出了一种全变分正则化非局部均值地震数据降噪算法，该算法可以有效去除非局部均值降噪算法带来的抖动效应，并有效保护细节，这对含有丰富的同相轴细节的地震数据降噪有重要的意义。

2 非局部均值算法简要回顾

对于大小为M×N且含有加性高斯白噪声的地震数据，在i点的含噪地震数据gi的观测模型为：

gi=ui+ni

(1)

(2)

设wi,j表示在搜索邻域中Pi和Pj之间的权值，0≤wi,j≤1，它等价为求解式(3)所示的最小化约束问题：

(3)

其中，uNL表示使用非局部均值算法降噪后的结果，权值wi,j的表达式为：

(4)

Zi为点i的归一化常数，g(Pi)、g(Pj)均表示邻域内的灰度值，d用于确定2个大小均为|P|的邻域Pi和Pj的灰度值之间的欧氏距离,距离较远的权值较小，距离较近的权值较大。h为滤波参数，通过控制指数函数的衰减速度，从而控制平滑程度，且h>0。

传统非局部均值算法中，滤波参数h取值过大或过小都会影响降噪效果，本文基于2个含噪地震数据块欧氏距离平方之间的统计规律，结合权重函数式和高斯分布函数表达式，将权重表达式更改为：

(5)

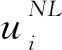
(6)

其中，E(d)为均值，Var(d)为方差。

3 去除抖动效应的非局部均值算法

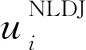
(7)

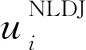
(8)

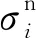
(9)

去抖动的非局部均值降噪结果可以表示为：

(10)

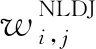
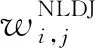
(11)

当i=j时,δi,j=1，其他情况δi,j=0。

4 全变分正则化非局部均值地震数据降噪

降噪后的地震数据表达式如式(12)所示：

(12)

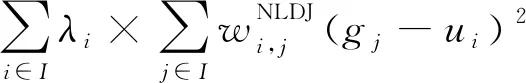
(13)

其中，γ是一个固定参数，用于确定自适应正则化的强度。

对地震数据的每个点i，进行如下步骤：

(3)迭代结束，进行最小化约束，得到地震数据的降噪结果。

5 地震数据降噪实验

现对合成地震及陆上叠后地震数据进行降噪，并用非局部均值NLM(Non-Local Means)算法、基于最近邻选择策略的非局部均值NN-NLM(Nearest Neighbor Non-Local Means)算法、本文的全变分正则化的非局部均值R-NLM(Regularization Non-Local Means)算法分别降噪。所有算法确保参数相同。本文对地震数据降噪的评价采用主观评价和客观评价相结合的方式，并使用峰值信噪比PSNR、均方误差MSE和平均结构相似性MSSIM来评价地震数据的降噪效果。

5.1 合成地震数据降噪

合成地震数据共计128道，分别加入均值为0、噪声水平分别为原地震数据幅值5%，10%，15%，20%的随机噪声,使用3种算法对含有15%的合成地震数据分别进行降噪，降噪结果如图1所示。

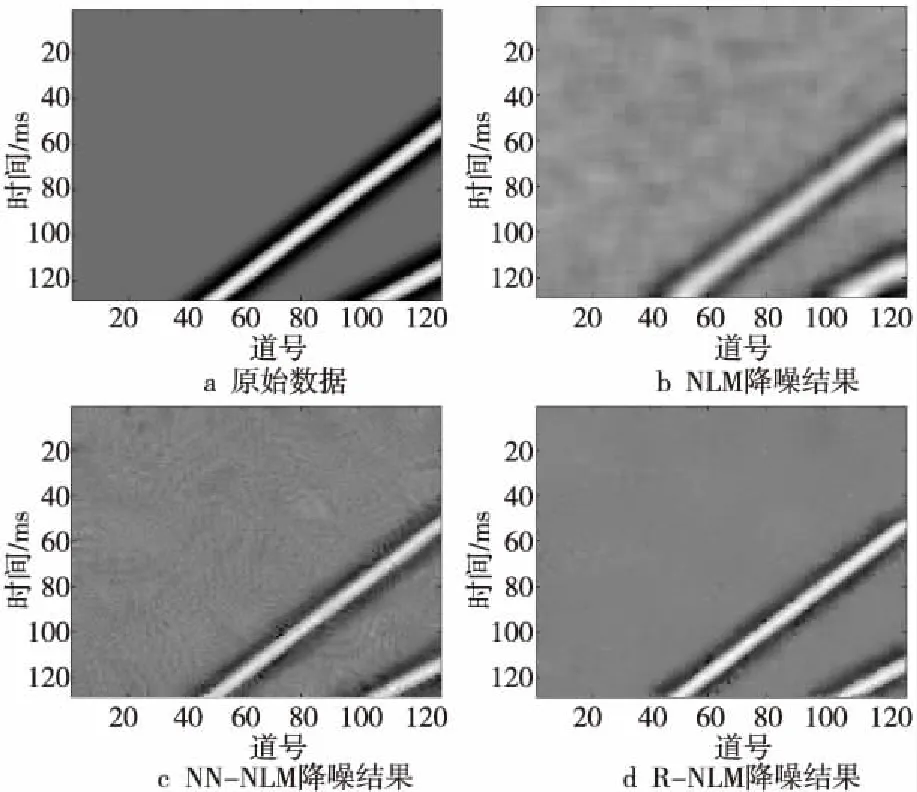
Figure 1 Noise reduction results of synthetic seismic data图1 合成地震数据降噪结果

在图1b的NLM算法降噪结果中，在去除噪声的同时，整体地震数据同相轴细节和背景区域都被过度平滑；图1c的NN-NLM算法降噪结果中，背景区域出现噪声残留斑块，同相轴细节较图1b明显；图1d的降噪效果良好，无明显噪声残留，合成地震数据的同相轴细节比较完整清晰，更接近原始地震数据。

为定量分析各算法的降噪性能，现人为添加均值为0、噪声水平分别为原地震数据幅值5%，10%，15%，20%，25%的加性高斯白噪声进行实验，各降噪算法得到的PSNR，MSE，MSSIM等性能指标如表1所示。

随着噪声比例增加，3种算法的PSNR值都在下降，而R-NLM算法降噪后的PSNR明显高于NN-NLM算法和NLM算法的，说明R-NLM算法在合成地震数据降噪方面表现良好；随着含噪比例的增加，3种算法的MSE值都在上升，NN-NLM算法只在高信噪比时表现良好，在含噪比例提升至10%后，R-NLM算法的MSE明显低于其他2种算法的，且增势较缓，表明R-NLM算法在合成地震数据降噪中具有优势。

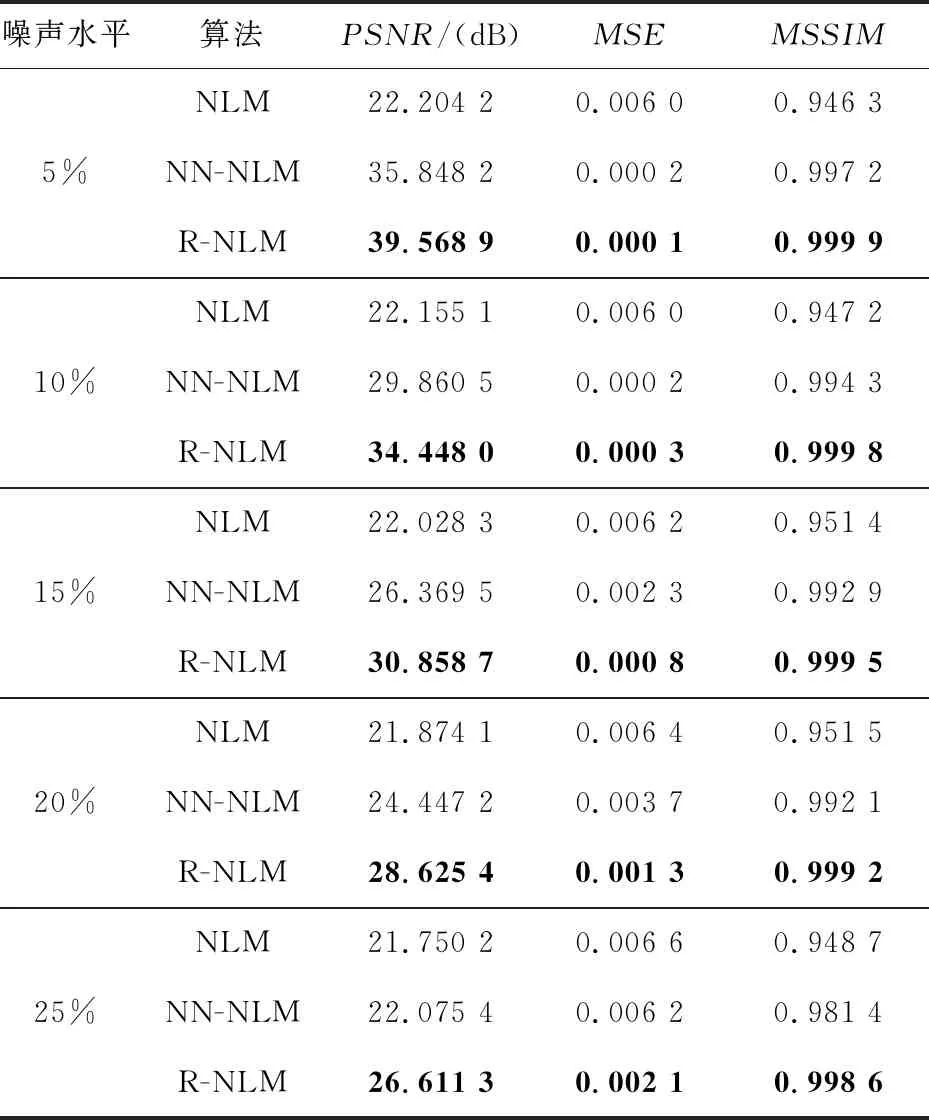
Table 1 Noise reduction results of synthetic seismic data表1 合成地震数据的降噪结果

5.2 陆上叠后地震数据降噪

某陆上叠后地震数据如图2所示，共计128道，单道含128个采样点。

Figure 2 Onshore post-stack seismic data图2 陆上叠后地震数据

为定量分析各算法的降噪效果，现人为添加均值为0、噪声水平分别为原地震数据幅值5%，10%，15%，20%，25%的加性高斯白噪声。图3所示为3种算法的PSNR值和MSSIM值随噪声水平变化的结果。

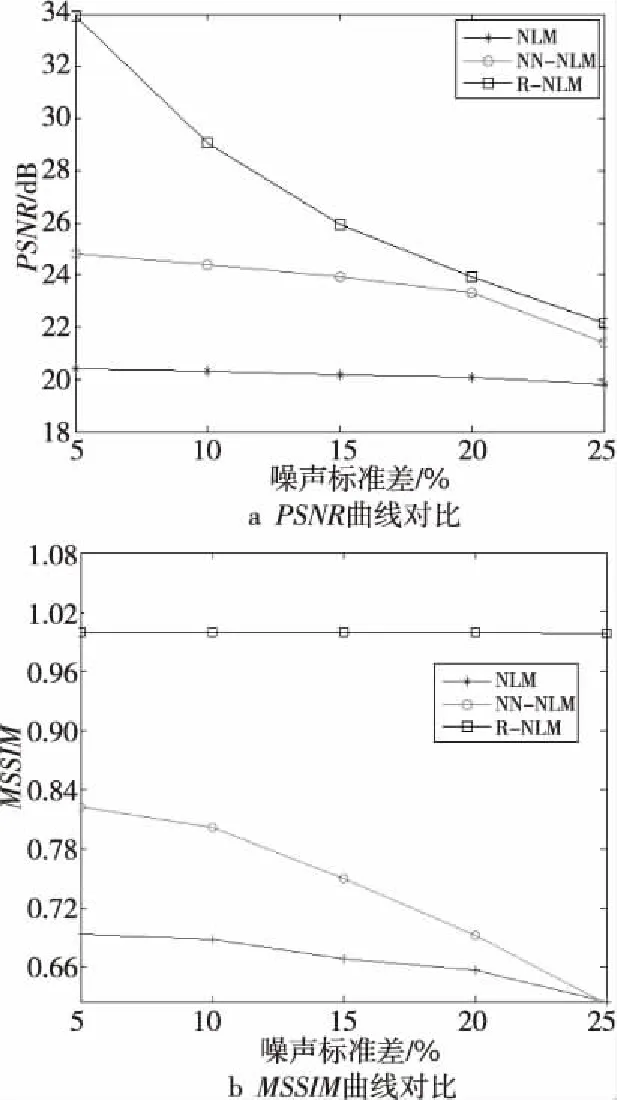
Figure 3 Experimental results comparison of 3 algorithms for onshore seismic data图3 陆上地震数据中3种算法的实验结果对比

由图3可知，R-NLM算法的PSNR值远高于其他2种算法的，在高信噪比时优势明显，在低信噪比时，R-NLM算法仍比其他2种算法优势明显，R-NLM算法的MSSIM值能较为稳定地保持在0.99以上，说明R-NLM算法降噪结果在3种算法中和原图像最为相近。

6 结束语

本文提出一种全变分正则化的非局部均值地震数据降噪算法，将权值函数进行迭代更新，从而有效去除非局部均值降噪带来的抖动效应，最后对结果进行全变分正则化。在合成地震数据和陆上叠后地震数据的降噪实验中，本文算法能够在降噪后保留较高信噪比的同时，有效保留地震数据的同相轴细节，降噪后的地震数据平均结构相似度均可保持在0.99以上，表明了本文算法在地震降噪中的有效性。然而，在保证计算效果的同时如何提高计算速度，仍然是以后研究的方向。