基于插值的高维稀疏数据离群点检测方法*

陈旺虎，田 真，张礼智，梁小燕，高雅琼

(西北师范大学计算机科学与工程学院， 甘肃 兰州 730070)

1 引言

数据驱动方法在规律发掘、趋势预测中发挥着越来越重要的作用。由于数据质量对数据分析的结果有很大的影响，在对数据进行分析前，往往需要过滤原始数据集中存在的异常数据。离群点通常被认为是偏离其他对象的个体，以至于人们怀疑是由另一种机制产生的[1]。因此，离群点子集往往与其余数据表现得不一致[2]。离群点检测是异常数据检测中的核心问题[2]，具有重要的研究意义。

监督学习是当前应用较为广泛的一类离群点检测方法[3 - 5]。但是，在实际的离群点检测任务中，异常样本的提供或者选择往往存在一定的难度。 如果样本对于离群点特征的覆盖不够，则严重影响此类方法的检测准确率。无监督的离群点检测方法由于不依赖于标签数据，与有监督的方法相比，其使用条件更为宽松，可应用性也更强。在无监督的离群点监测中，基于聚类的方法一直以来是一个重要的研究分支。在此类方法中，当前的研究方法大多依靠不同的策略，通过改进初始聚类中心等手段来不断改善聚类效果，从而提高离群点检测的准确率。

然而，从数据的空间分布角度来看，高维数据很多时候具有稀疏性。因此，基于距离或者密度思想的聚类，容易导致一些非离群点数据被排除在聚类所获得的各个簇中，降低了离群点的召回率。另一方面，增加距离或者密度阈值虽然可以在一定程度上提高离群点的召回率，但又容易导致离群点数据与正常数据的交织，降低离群点检测的准确率。综上，本文针对高维稀疏数据，基于空间数据插值的思想，引入空间样本的遗传变异策略，试图探索一种无监督的离群点检测方法。

后续的内容安排如下：第2节对当前的相关工作进行了介绍和分析；第3节提出了一种基于插值的高维稀疏数据离群点检测方法，并在第4节中，对基于遗传算法的插值方法进行深入分析；第5节在对实验结果分析的基础上，对所提方法进行了比对评价；最后，在第6节中，给出了本文的结论以及对将来工作的展望。

2 相关工作

有监督的离群点检测方法通常从样本数据中学习并建立正常样本或者离群样本的模型。通过建立假设模型h(x)并确定阈值ρ，当给定样本x，若h(x) ≥ρ，则认为x是正常样本，否则认为其是离群值，而离群值在很多情况下也被认为是异常样本，并且阈值ρ往往根据经验误差设置[5]。现有的大多数离群点检测方法都可认为是基于该框架的，针对假设模型具体构建方法不同，演化出了不同的有监督离群点检测，代表性的工作包括文献[5 - 8]。

通常来讲，基于监督学习的离群点检测方法具有较高的准确率，但其准确率对于样本的数量和标注质量仍具有很高的依赖性。从某种程度上看，样本的数量和标注质量，决定了此类方法的检测效果。然而，大量样本的标注是一项很有挑战性的工作，这对于有监督的离群点检测造成了诸多困难。在很多情况下，也限制了此类方法的实际应用。

非监督离群点检测方法通常不需要样本标注，与基于监督学习的离群点检测方法相比，其应用条件更为宽松。常见的一种思路是通过参数化或非参数化方法估计训练样本的密度模型，并设置相应的密度阈值，通过判断局部的密度来确定离群点[9]。当前的无监督离群点检测方法中，比较有代表性的包括基于相对密度估计的检测方法、基于模型的检测方法和基于支撑域的检测方法。

基于相对密度的离群点检测方法可以有效地解决数据对象密度分布不均匀的问题[10]。在基于相对密度估计的方法中最具代表的是LOF(Local Outlier Factor)算法[11]，然而，这种方法有时对参数很敏感，并且密度估计方法对目标类数据的稀疏区域很难做出正确的判断。

基于模型的检测方法根据模型可分为3种类型。点重构方法利用样本点到最近聚类中心的距离作为重构误差来进行离群检测，代表性工作包括基于K-means[12]和K-center[13]的离群点检测。平面重构方法利用最近邻超平面的距离作为离群点检测的重构误差。正是考虑到点重构方法难以描述平面簇数据，Bradley等人[14]提出了K-plane clustering算法，类似工作还包括基于曲线、曲面和子空间重构的离群点检测方法。主成分分析PCA(Principal Component Analysis)[15]就是一种基于线性降维的方法，也可以通过扩展在非线性环境中使用(例如在文献[16]中提出的KPCA(Kernel PCA)方法)。PCA的另一种非线性扩展基于主曲线[17]，根据数据中每个点的重构误差以及一定经验误差约束下设定的阈值，构造以主曲线为中心的柱形数据描述。

由于在实际的离群点检测应用中，通常只有一种类型的样本，Scholkopf[18]利用单分类SVM提出了一种基于支撑域离群点检测的方法。该方法为避免受到噪声数据和孤点数据的影响，不严格要求训练样本到球体中心的距离的平方小于或等于R2，但大于R2的点将受到惩罚。在此基础上，Tax等[19]提出了支持向量数据的描述。

上述无监督的离群点检测方法，为本文的研究奠定了很好的基础。但是，在样本数量有限的情况下，数据的空间分布表现出很高的稀疏性，给基于密度、模型以及支撑域的离群点检测造成了很大的困难。事实上，高维样本在空间分布上往往具有天然的稀疏性。然而在当前的研究中，针对高维稀疏数据的离群点检测关注不多。因此，本文引入高维数据空间的插值思想，试图探索一种针对高维稀疏数据的离群点检测方法ODGA(Outlier Detection for Genetic Algorithm )。

3 基于插值的稀疏数据离群点检测

通常认为，离群点对象与其他对象存在较大的差异，以至于可怀疑其是由另一种机制产生的。因此，离群点检测可被用于异常数据的检测。假设对所有样本数据进行了聚类，则每一簇中的样本具有相似的特征，而样本点与质心的距离超出一定范围时，将很难被归入到任何一个簇中，可认为该样本的产生机制可能与绝大多数样本存在差异，从而在很大概率上属于离群点。

无监督聚类方法简单，依赖条件宽松。其中，K-means是具有代表性的基于距离的聚类算法，是当前应用最为广泛的聚类算法之一。K-means以距离作为样本相似性的评价依据，距离越近，认为样本的相似性越高，其可认为是寻找紧凑的、独立的簇。因此，本文的离群点检测方法首先基于K-means聚类，通过判断样本点是否大于一定的阈值来检测离群点。

然而，由于K-means算法以距离平均值作为聚类中心，并将其应用到下一次迭代中，当聚类中心是噪声点或孤立点时，将使得聚类中心偏离数据集的密集区域。因此，如果数据集包含大量孤立点或噪声数据，聚类结果受噪声或孤立点的影响较大，导致聚类结果不准确甚至不正确，从而导致分离出来的离群数据与正确的离群数据产生较大偏差。如果直接用传统K-means算法进行离群点检测势必会导致大量的离群点影响聚类结果，从而使得无法有效分离出离群值和正常值，在检测出越多的离群点的同时增大正常点的损失。当样本数据比较稀疏时，这种情况表现得更为突出。

因此，本文在借鉴K-means算法的基本思想的基础上，引入空间数据的插值思想，尽量阻止稀疏数据在聚类的时候被合并，以提高离群点的检测效果。该方法的基本思想如下所示：

(1)将所有样本作为现有样本集中的初始总体，随机选取初始聚类中心完成一轮聚类。

(2)在聚类产生的簇中，依靠适应度函数找出子簇中聚类效果最差的一个类。

(3)对上述类的样本空间进行插值，并进入下一轮聚类。

(4)在最终的聚类结果中，与质心的距离过大的样本点被认为是可能的理论点。

ODGA方法的伪代码可描述如下：

输入参数：k,path,column,n,Runtimes,Gtimes,geneticrate。

1.variarate=readConfiguration();

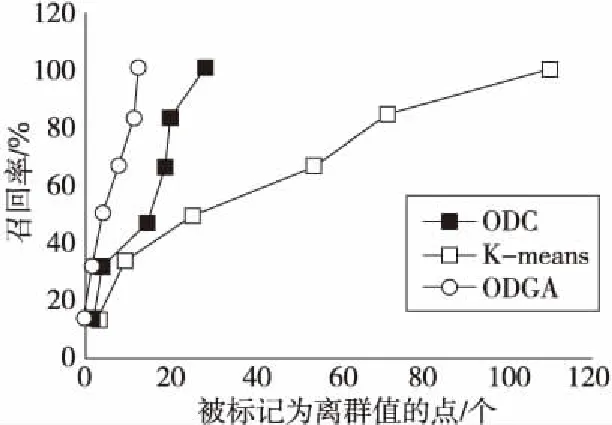
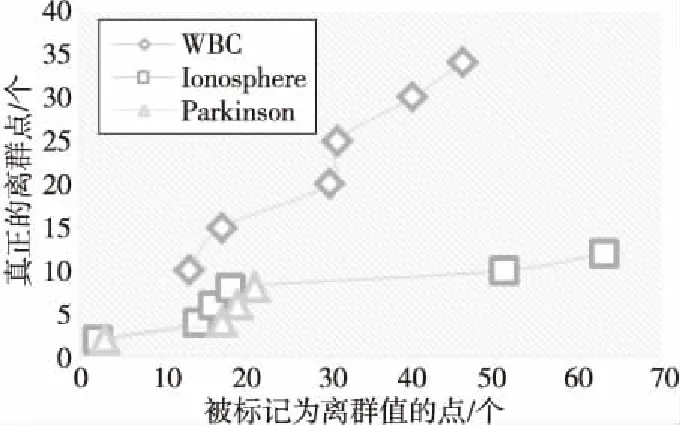
2.foreachi

3.Initializedata() ;// 初始化数据

4.scope=k_means(K,path,column,n);

5.forj

6.Genetic_Algorithm(scope,geneticrate,variarate,column,n); /*遗传变异算法*/

7.j++;

8.endfor

9.k_means(k,path,column,n);

10.Statistic(k,i); // 统计实验结果

11.i++;

12.endfor

1.functionk_means(k,path,column,n)

2.scope=Getscope(path,column)；/*scope是一个二维数组，其值为数据中每个属性的取值范围*/

3.central=Greatingrandomcentral(scope,k)；/*随机获得簇中心*/

4.whileIstabilized()do

5.classify(central,path)；//按照簇中心分簇

6.central=Findnewcentral()；//寻找簇中心

7.endwhile

8.returnscope

9.endfunction

4 基于遗传算法的稀疏数据插值

由于遗传算法是一种全局优化算法，因此选择遗传算法对K-means聚类算法进行优化。与传统的优化方法(枚举、启发式等)相比，遗传算法以生物进化为原型，具有较好的收敛性，具有计算时间短、鲁棒性强等优点。将遗传算法应用于本文方法的最大优点是在高维稀疏样本集的离群点检测中，弥补了数据信息不完整的不足。通过合理产生新数据样本来增加数据密度，帮助找到更有利的质心。

遗传算法是一种模拟自然环境中生物遗传和进化过程的自适应全局优化概率搜索算法。遗传算法将搜索的变量看作有限长度的字符串，这些字符串被称为染色体，这些字符串的单个元素或特征被称为基因，基因的值被称为等位基因[20]。在ODGA方法中，我们使用二进制编码方式，将每条数据视为一条染色体，每条染色体由L个基因组成，其中基因L表示属性。在二进制情况下，编码染色体的每一位都被初始化为随机的0或1。

本文使用了单点交叉与固定交叉概率pc，这意味着群体首先随机配对，然后随即设置交叉点，最后选择配对的2条染色体之间的部分基因进行交换。在单点交叉中，在对应点处将2个“父母”切割一次，并且交换切割后的基因片段。突变是为了有助于在后代染色体中引入多样性，通过修改一些基因引入新的遗传结构。在二进制情况下可以通过以小概率反转每个基因的值来完成简单的突变，通常突变概率pm由pm=1/L得到，其中L为染色体长度。

构造恰当的适应度函数对优化算法的性能具有重要的影响，本文使用类内距离与类间距离的比值来定义适应度。显然，如果每个类之间的距离越大，同一类内的距离越小，适应度函数值越小，则聚类效果越好。

如果将每个集群总体的样本集表示为xc，s0,s1,…,sm-1为集群xc中的数据。

每个簇内的平均距离dc(x)表示为：

其中，c表示质心，m表示集群样本数。适应度函数为：

其中，ki,j表示类间距,n表示簇的个数，

本文通过遗传变异和聚类这2个阶段的融合迭代，对原始数据的稀疏部分进行了插值处理，利用这些新数据填充原始样本集的稀疏部分，改善了稀疏数据在进行聚类的时候容易被合并的问题，在得到更好的聚类结果后再进行离群点的检测。该部分的伪代码描述如下所示：

1.functionGenetic_Algorithm(scope,geneticrate,variation,column,Gafile,Tfile)

2.gedata[][]=readData(Gafile,geneticrate);

3.parents[2][]=nextParents(gedata);

4.an=getAttributionNumber();

5.whileparents≠nulldo

6.crosspoint=random(0,an)//an表示数据的维度

7.newdata[][]=regroup(parents,crosspoint);

8.writeData(newdata,Tfile);

9.parents[2][]=nextParents(gedata);

10.endwhile

11.whilei

12.variapoint=random(0,an);

13.varieddata[i][variapoint]=random(scope[0][variapoint],scope[1]variapoint);

14.writeData(newdata,Tfile);

15.parents[2][]=nextParents(gedata);

16.endwhile

17.endfunction

5 实验分析

为验证本文方法对高维稀疏数据中离群点的检测效果，从UCI公共数据集[21]中选取了Lymphography、WBC、Ionosphere和Parkinson 4个数据集，对文中方法的有效性进行了实验分析，同时与当前的离群点检测方法进行了对比分析。需要说明的是，由于当前没有公认的离群点检测的公共数据集，通常的做法是对机器学习数据集进行采样，将离群点数量控制在总数据量的5%左右。本实验最终选择和构造的离群点检测的数据集如表1所示。

Table 1 Outlier detection sample dataset表1 离群点检测样本数据集构成

以Lymphography数据集为例，共包含148个实例，每个实例由18个属性描述。该数据集总共有4类标签，分别表示该样本描述的个体的淋巴为正常、转移、恶性和纤维化4种情况。与文献[22]类似，最小的2个类中的实例数仅占数据集中实例数的4.05%，其中的样本将被认为是离群点，相应地，其他2个类中的实例被认为是正常样本值。WBC、Ionosphere、Parkinson 3个数据集中的离群点标注采用了相同的方法。

从某种角度来看，离群点检测可被看作二分类问题。如果将离群点看作是异常值，其余点则为正常值，检测方法就可以作为一个分类器将所有数据分为异常和正常2类。而对于二分类问题，样本可以分为真阳性(TP)、假阳性(FP)、真阴性(TN)和假阴性(FN)，由此可得出表2所示的混淆矩阵。基于混淆矩阵可以计算分类器的准确率，而准确率越高，则认为分类结果越好。因此，该指标也可用于评价异常检测方法的准确性，其计算方法如下所示：

Table 2 Confusion matrix表2 混淆矩阵

ORC(Outlier Removal Clustering)[23]、FindCBLOF(Find Cluster-Based Local Outlier Factor)[23]和ODC(Outlier Detection based Clusering)[22]方法都是基于改进的聚类算法的异常检测方法，本文在Lymphography数据集上，对上述3种方法与本文方法从分类器的角度进行了比较，如表3所示。从图1可以看出，本文方法ODGA的准确率为83.11%，而ODC、FindCBLOF、ORC 3种方法的准确率分别为66.22%,63.51%,50%，ODGA的准确率(Accuracy)明显高于其他3种方法的。

Table 3 Test results of four approaches表3 4种方法的检测结果

Figure 1 Comparison of accuracy图1 准确率对比

如果以TPrate表示阳性样本被分成阳性样本的比例，FPrate表示阴性样本被分成阴性样本的比例，则Euc可用以表示分类器在ROC图上与理想分类器之间的距离，Euc值越小表明分类器越好。也就是说，可以用Euc表示离群点检测方法的检测精确度(Precision)，其中：

图2表明，与其他3种方法相比，ODGA方法的Euc值最小，并且明显优于其他3种方法，进一步说明本文方法具有更好的分类效果。

Figure 2 Comparison of classification precision图2 分类精确度对比

由于ODGA基于K-means聚类，并引入了插值思想，来提高稀疏数据的离群点检测效果，实验中，将ODGA与传统的基于K-means的离群点检测方法进行了比对分析。另外ODC[21]是典型的基于改进的K-means的离群点检测方法。该方法首先将每个点分配给距离最近的质心，如果检测到离群值，则将其从数据集中删除，并且当作离群点另外存储，接下来重新计算质心，直到没有样本点从一个类移动到另一个类中时，迭代停止。该方法界定离群点时采用了如下原则：当样本点与质心之间的距离是该簇中所有样本点与质心距离平均值的固定倍数时，则认为该点为离群点。因此，本文对ODGA方法与ODC方法进行了进一步的比对分析。

鉴于Lymphography数据集不需要采样就符合我们对离群点占比全部数据的5%的要求，本部分实验中使用了Lymphography数据集。如图3所示，横坐标表示检测后被标记为离群点的所有点的数量，纵坐标表示召回率。可以看到，当K-means方法找到所有真正的离群点(召回率为100%)时，共标记出110个离群点，其中误判104个点；ODC方法共标记28个，误判22个。ODGA方法一共将13个样本点标记为离群点，其中只有7个点被误判。从这个角度来看，ODGA方法的检测准确率明显优于基于K-means的离群点检测方法和ODC方法的。

Figure 3 Recall comparison of three algorithm图3 3种方法的召回率比较

由于K-means算法初始聚类中心是随机选取的，因此每个算法的初始质心都会发生变化。我们将ODC、ORC和FindCBLOF应用于Lymphography数据集10次，初始簇中心均不同，且都是在数据集中随机选取，实验表明这些离群点基本全都位于每个簇中距离质心较远的位置。如图4所示，ORC方法[23]在被认为是离群点的40个点中准确找到6个实际的离群点；FindCBLOF方法[23]在被标记为离群点的30个点中找到6个真正的离群点；ODC方法[22]在标记的28个点中找到6个真实的离群点。然而，ODGA方法仅标记了13条数据为离群点，并包含有全部的6个离群点。由此可以得到结论，与其他3种方法相比，本文方法不仅达到了100%的召回率(查找所有稀疏类实例)，而且最大限度地缩小了标识离群点的范围。

Figure 4 Comparison of outlier detection approaches on Lymphography dataset图4 在Lymphography数据集上离群点检测方法的比较

为了观察在面对不同数据集时，本文方法是否还能保持较好的检测效率。针对表1中的WBC、Ionosphere和Parkinson 3个数据集，对本文方法进行了进一步的测试。从图5可以看出，在WBC数据集上，被标记为离群点的46条数据中涵盖所有正确的离群点，Ionosphere数据集和Parkinson数据集上本文方法同样均表现良好。

Figure 5 Test ODGA on multiple datasets图5 在多个数据集上测试ODGA

综合上述实验分析，通过利用遗传算法对原始样本数据集的稀疏部分进行插值处理，解决了稀疏数据在聚类时容易被合并的问题，明显改善了聚类效果，从而提高了离群点检测的准确率和精确度。

6 结束语

本文探讨了一种适用于高维稀疏数据集的离群点检测方法。该方法借鉴生物学中种群繁衍的规律，引入插值思想，解决了K-means聚类中稀疏数据容易被合并的问题。实验表明，该方法能够有效检测出离群点。

在将来的工作中，我们将进一步探索检测到的离群点的生成机制。