基于闭合排队网络扩展求和算法的露天矿车铲协同优化研究

赵加征 李 宁，2 叶海旺，2 王李管 王其洲，2 雷 涛，2

（1.武汉理工大学资源与环境工程学院，湖北武汉430070；2.矿物资源加工与环境湖北省重点实验室，湖北武汉430070；3.中南大学资源与安全工程学院，湖南长沙410083）

露天开采具有基建时间短、生产能力大、开采成本低、作业安全性高等优点，在现代矿业开发利用过程中得到了广泛应用［1］。由于汽车运输具有调度方便、适应范围广等优点，是目前露天开采的主要运输方式。据统计［2］，露天开采运输作业成本约占矿石开采总生产成本的60%，极大影响着矿山企业的经济效益。因此，在满足矿山生产能力的条件下，有效减少运输车辆的等待时间，确定车铲最优配比，提高汽车运输效率，对于提升矿山经济效益具有重要意义。

排队论是研究服务过程中排队现象的一种数学理论，也称为随机服务系统理论［3］。排队理论能够从系统整体角度描述作业过程，在很多领域得到了应用［4-9］。近年来，大量学者利用排队理论研究并分析了露天矿运输作业过程的排队现象。高景俊等［10］应用排队论中的有限队列模型优化了排岩系统的工艺流程，结合生产实际情况来控制车铲合理调配。俞雄志［11］采用排队理论确定车铲比，并比较了不同车铲配比之间经济效益的差异性。Ercelebi 等［12］采用闭式排队网络理论对卡车进行了分配，基于线性规划实现了汽车的运行调度，并分析了运输作业中卡车数量与最优调度策略对成本的影响。Ta 等［13］为确定装载机组的最少卡车数量，以吞吐量及矿石品位为约束，基于有限源队列理论，建立了油砂露天矿排队模型，跟据装载机闲置概率与卡车数量之间的关系，建立了卡车分配模型来解决实际问题。

上述研究大多假设作业时间服从负指数函数分布，采装过程仅考虑单台装载设备。然而实际生产中只有卸矿作业时间服从负指数函数分布［14-15］，装车时间基于负指数函数分布的假设可能会导致计算结果与实际情况产生较大差异［16］，不同排队模型也会影响卡车等待时间［17］。矿山在同一工作平台一般具有多个装载点，运输汽车数量需根据作业计划进行选择。为研究多铲车、作业时间服从一般函数分布的情形，引入闭合排队网络扩展求和算法计算矿山生产处于稳定状态时各系统的运行指标。

1 闭合排队网络扩展求和算法

求和算法（Summation Algorithm，SUM）是一种分析计算服务时间呈负指数函数分布排队网络的近似算法，在此基础上改进得到的扩展求和算法（Extended SUM，ESUM），可以有效解决服务时间为一般函数分布的排队网络问题［18］。

1.1 ESUM计算原理

假设某闭合排队网络中有N个服务点，第i个服务点（1 ≤i≤N）有mi个相同的服务台，此闭合排队网络中顾客总数为K。闭合排队网络处于稳定时，有如下关系成立：①各服务点的平均排队长度与该服务点流量有关；②各服务点内平均排队长度之和与闭合网络内顾客总数相同。

第一类关系可表述为

SUM将服务点分为4类，如表1所示。

注：m表示该服务点共有m个服务台；∞表示该服务点存在无数个服务台。

根据上述分类，有下式成立：

式中，m i为第i个结点处包含的相同服务台数量；ρi为第i个服务点的服务强度；Pmi为表 1 中 Type1 型系统中全部服务台都被占用的概率。

第二类关系可表述为

式（1）、式（3）构成了SUM算法的基础。

在ESUM 中，Type1 的服务时间函数分布由负指数分布扩展到一般分布，引入系数ai对式（2）进行修正：

对于 M/G/1-FCFS 和 M/G/m-FCFS 型服务点，平均排队长度分别为

ESUM算法的迭代步骤为：

（1）以λ1= 0 为流量下限，λμ= min{μi,mi} 为流量上限。对于-/G/∞型服务点，mi=K。

（3）若g(λ)＞K，令λμ=λ，若g(λ)＜K，令λ1=λ，重复步骤（2）；若(K-ε)≤g(λ)≤(K+ε)（ε是一个很小的数，表示计算精度），则停止计算。利用满足要求的流量λ，便可分析闭合网络中各服务点的运行指标。

1.2 改进ESUM算法

1.2.1 误差分析

矿山在实际生产过程中由于闭合网络中总卡车数量为定值，不存在无容量约束的情形，即最大排队长度应为卡车总数，而ESUM 算法是基于无限容量等待过程得到闭合排队网络的近似公式，无容量约束下可能会出现排队长度大于卡车总数的情形。利用Matlab 软件对文献［19］中卡车总数为5 辆时的流量进行随机模拟，模拟时间为500 min，在无容量限制情况下采装过程排队长度随时间的变化关系如图1 所示。由图1可以看出，卡车在采装系统中长度最高为8 辆，且有多次超过卡车实际总数5 辆。在无容量约束时，铲车处的排队长度会变大，导致闭合排队网络整体流量λ变小，导致直接应用式（5）、式（6）计算会产生较大误差。因此，采用有限容量的等待过程对ESUM算法进行改进，更符合矿山实际情况。

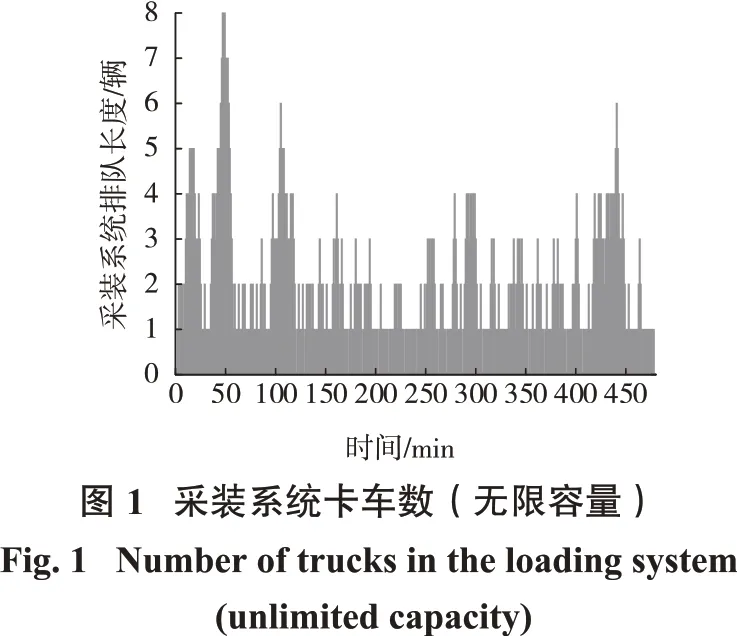
1.2.2 算法改进

矿山闭合网络模型中，卡车总数不变，当所有卡车都在同一服务点时，将后续卡车看作损失，没有加入排队过程，等待制排队模型变为混合制排队模型，利用此时的系统排队长度改进式（5）、式（6）确定模型表达式，即：

式中，bi为修正系数。

服务点多服务台与单服务台的差异，仅仅表现为卡车被铲车服务的随机性不同。鉴于多服务台情形的公式［3］过于复杂，因此本研究选用单服务台的情形进行近似分析。单服务台混合制排队模型M/M/1/N 和单服务台等待制排队模型M/M/1 的系统排队长度公式分别为

式中，N为排队容量；ρ为服务强度。

由式（9）、式（10）可得：

当ρ取值分别为 0．4, 0．5,0．6,0．7 时，h随卡车数量的变化情况如图2所示。

由图2 可知：随着卡车数量逐渐增大，M/M/1 模型和M/M/1/N 模型的比值越来越接近1，即当卡车数量无限大时，两种模型无差异。在ESUM 算法中，闭合网络中流量大小与卡车总数成正比，且ρi=λiμi，由此定义bi：①bi为ρi的函数，且当ρi= 0时，bi= 0；当ρi= 1 时，bi= 1；②bi为单调递增函数，且增长率逐渐减小。为简化公式，选常用函数，取。

1.2.3 方法验证

利用改进ESUM 算法对某矿山生产过程的随机模拟实例［20］进行分析，假设该露天矿山有1 台电铲，若干辆卡车，卸载场地有1 个卸矿车位，可供1 辆卡车进行卸车作业。计算机模拟基础数据为：装载时间服从正态分布，其均值为1.32 min，方差为0.072 9；重车运行时间服从定长分布，其均值为4 min；卸车服务时间服从负指数分布，均值为0.74 min；空车运行时间为定长3.67 min；每辆卡车装载量均值为22.5 t；每班工作时间为6 h。

针对卡车总数K= 5,6,…,11 的情形，分别采用改进的ESUM 算法对上述实例的闭合网络进行分析计算，并与原始算法的计算结果对比，如表2 所示。改进后的班生产能力与计算机模拟得到的生产能力差异在3%以内，精度相较之前明显提高。卡车总数在11 辆时的误差较大，主要是由于修正函数bi后期与函数h不完全符合，不过随着后期卡车数量增多，出现排队现象越明显，对于车铲协同不利，在实际优化时不会考虑此类数据，因此利用改进的ESUM 算法进行车铲协同优化具有可行性。

2 工程应用

2.1 矿山闭合排队网络模型

某年产280万t的露天石灰石矿山为满足生产需求，每天需连续工作两班共计16 h，平均班产量4 667 t。矿山现有单斗挖掘机3台，运输卡车12辆，其中11辆常用。矿山运输路径中段有一段单车道，并且卸矿前需要称重。实际生产中，在采装过程中极易排队等待现象。因此，有必要对车铲协同进行优化，减少卡车在采装过程中的等待时间，提高卡车利用效率。

依据闭合排队网络理论，将该矿山作业过程抽象为采装、重车运行、单车道、称重、卸矿、空车运行等系统，如图3所示。

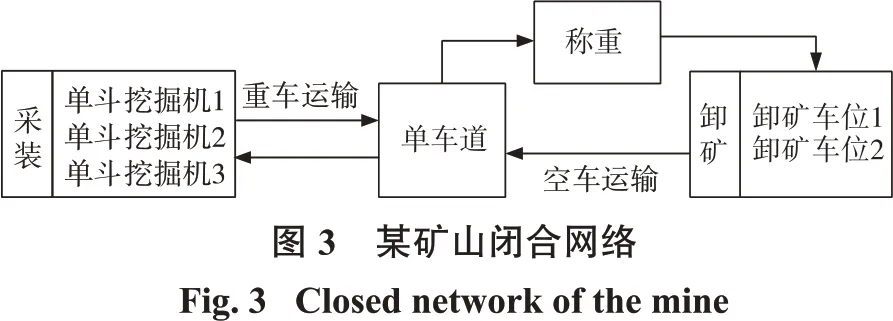
2.2 排队网络分析

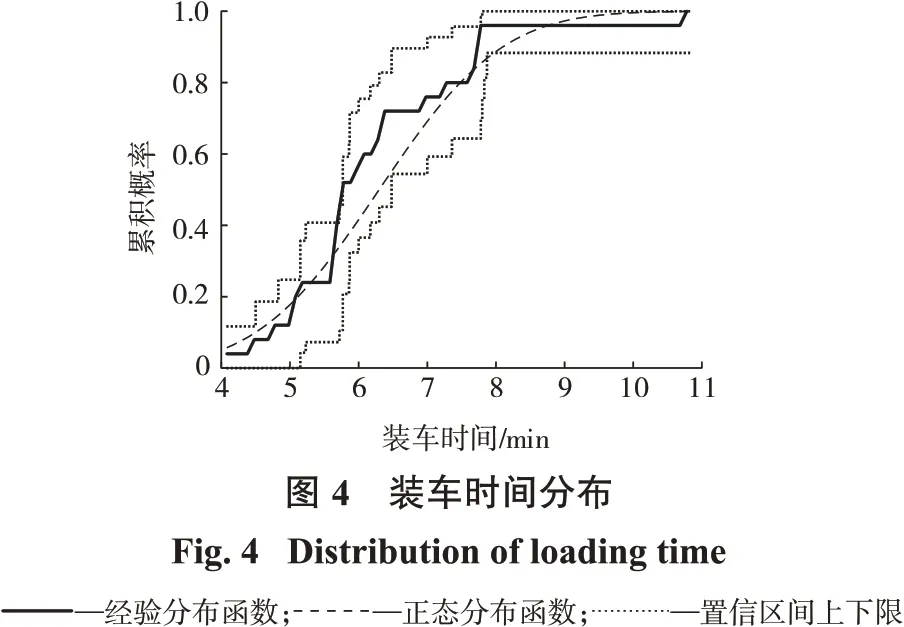
（1）采装系统。采装过程中，3 台单斗挖掘机在同一工作平台进行工作，卡车到达后可以自由选择空闲的挖掘机，当3 台挖掘机都被占用时，后来的卡车排列成一队等待。以人工计时方式对装车时间进行统计并利用Matlab 软件进行数据分析，结果显示，未通过K-S 检验，即装车时间不符合负指数分布；数据通过J-B正态分布拟合检验，装车时间经验分布函数如图4所示，置信度为95%。由图4可以看出，数据基本符合正态分布，因此，本研究将采装过程视为3个服务台的M/G/3 型排队系统，装车时间均值为7.298 4 min，标准差为1.404 2 min。

（2）重车运行系统。将矿山公路视为无限个服务台，即卡车在公路行驶时无需等待。为简化排队模型，将两段重车运行合成一段完整的运行路径，重车运行时间符合均值为2.6 min 的定长分布，此系统属M/G/∞型。

（3）单车道系统。在行驶路径中间部分的单车道，只允许单向通过。车辆在启动加速阶段时所用时间较长，在平稳路段运行时可以认为是匀速运动。该部分可以双向通行，此系统的流量应为2λ，通行时间为定值0.5 min，属于M/G/1型排队系统。

（4）称重系统。卡车经过重车运行后，在卸矿前需先进行称重。矿山目前有1台地磅，称重过程耗时均值为0.5 min，据以往经验［15］，称重时间服从负指数分布，此系统属于M/M/1型。

（5）卸矿系统。该矿山目前只有1 个卸矿点，可允许2 辆卡车同时进行卸矿作业，即系统内有2 个服务台，卸矿时间服从均值为2 min 的负指数分布，此系统属于M/M/2型。

（6）空车运行系统。与重车运行类似，可以将该系统视为含有无数个服务台的服务点，服务时间定长分布的M/G/∞型排队系统。空车运行时间均值为2 min，其中不包括在单车道的运行时间。

卡车在此矿山闭合网络模型中循环经过6 级服务系统，根据各系统排队类型，选用相应公式，即可求解出闭合网络处于稳态时各服务点的运行指标。

2.3 改进ESUM模型计算结果

2.3.1 闭合排队网络各节点分析

用改进ESUM 算法求解该矿山闭合排队网络模型中K= 4,5,…,14 的近似解，计算精度取ε= 0．001，结果如表3所示。

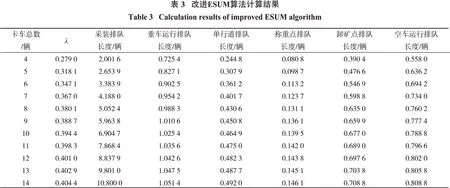
当K为 6～14 时，增加的 8 辆卡车有 7 辆在采装系统中，说明这些卡车以排队等待的形式加入到网络中。随着卡车数量增加，λ值明显变大，不过其增长率逐渐减小。由图5 可知：λ值会趋近于采装过程极限服务能力，即采装过程容易成为限制整个闭合排队网络流量增加的节点，因此需要对采装过程的排队指标进行精确分析。

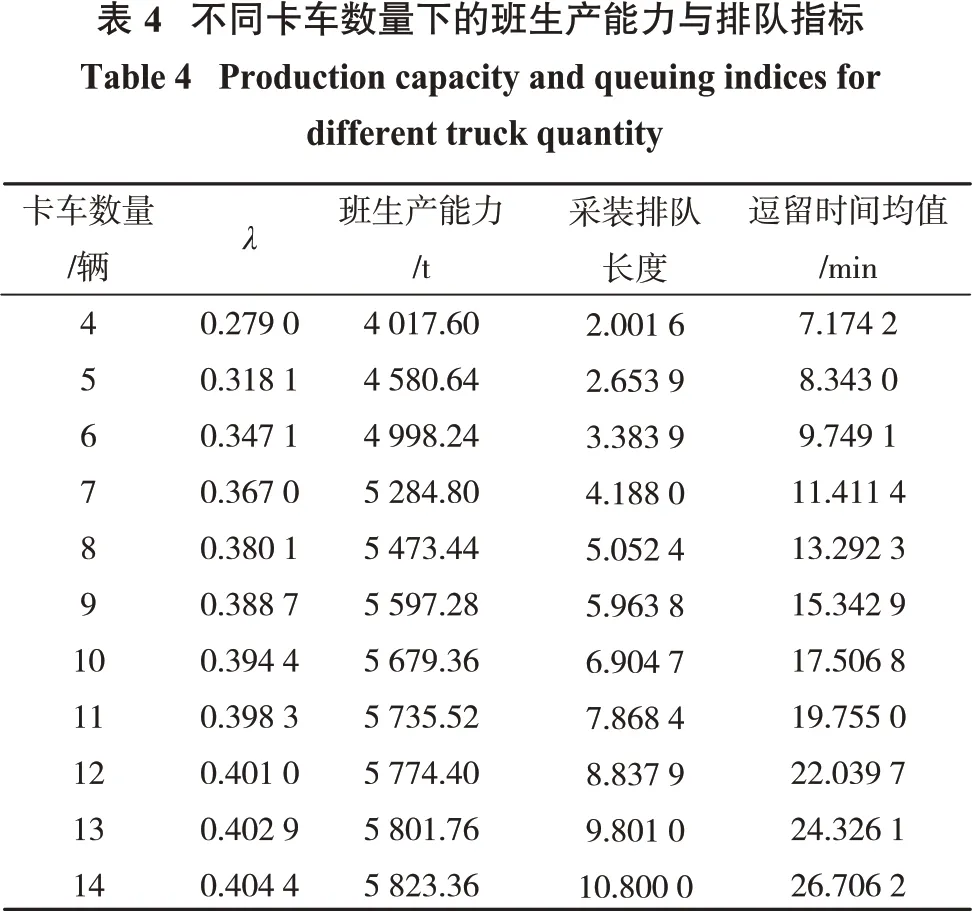
2.3.2 采装过程分析

假设卡车以恒定到达率到达采装点，卡车装载量均值为30 t，计算每班生产能力并依据Little公式［3］计算各到达率对应的平均逗留时间，结果如表4 所示。当卡车数量为4、5时，卡车在采装系统平均逗留时间较少，但此时该系统中的平均卡车数小于3 辆，即单斗挖掘机可能会存在空闲时间过长的情况。卡车总数为6 时，单斗挖掘机在平均意义上无空闲，卡车逗留时间也较短，同时满足平均班产量目标，此时车铲协同效果较优。考虑到实际生产过程存在其他未考虑的因素，因此卡车总数为7辆比较适宜。卡车数量从原先的11 辆减少至7 辆时，卡车在采装过程的逗留时间缩短了42.24%，班生产能力只减少了7.86%。

2.4 随机模拟验证

利用Matlab软件模拟采装系统的排队过程，以验证采用改进ESUM 算法确定卡车数量的合理性，当两者在采装系统的数量一致或相差不大时，可以认为改进ESUM 算法有效。模拟过程需要进行有效性检验，一般情况下排队过程达到稳定时的排队指标可以通过理论推导得到，但M/G/m/N排队模型用数学推导异常困难，M/M/m模型与M/G/m模型的仿真模拟差异只是生成服务时间随机数的函数不同，可以转化成为M/M/m/N 排队模型进行验证［21］。本研究根据实例［3］分析该随机模拟的准确性。

设计算机有5 个终端，用机时间服从负指数分布，为15 min；顾客到达符合泊松流，平均0.2 个/min；5 个终端全被使用时，后续顾客只能前往别处。根据排队论公式计算上述示例，系统平均排队长度为2.669 7个，平均逗留时间为15 min。采用上述模拟方法模拟多次发现，系统平均排队长度为2.76 个，平均逗留时间为15.59 min，可以证明该模拟有效。

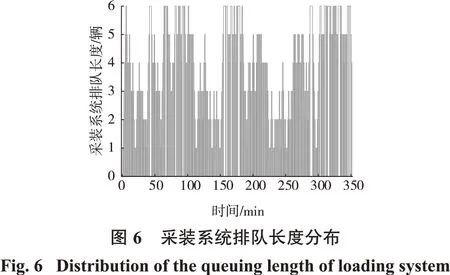
运用上述模拟方法对改进ESUM 算法的计算结果进行验证，当卡车总数为6 辆时，分别模拟10 次采装过程，模拟时间均为500 min，结果如表5所示，某次排队长度随时间的变化特征如图6 所示。10 次随机模拟中采装系统平均排队长度的平均值为3.204 8，改进ESUM 算法的计算值为3.383 9，可以认为由改进ESUM算法计算得到的卡车数量较准确。由图6可以直观看出，卡车数量保持在3辆时次数较多。

3 结 论

根据实际情况建立了某露天矿生产的闭合排队网络模型，将该矿山流程简化为采装、重车运行、单车道、称重、卸矿和空车运行等系统节点，研究得到如下结论：

（1）引入闭合排队网络扩展求和算法，计算稳态时该矿山各系统节点的运行指标，得到采装过程是制约该矿山生产的瓶颈环节。

（2）以卡车等待时间少并满足平均班产量为目标，确定该矿山合理的卡车数量为7 辆，卡车在采装过程中的逗留时间较未优化前缩短了42.24%。

（3）利用仿真模拟验证了闭合排队网络扩展求和算法在该矿山应用的可行性，结果表明，采用此方法进行车铲协同优化简单有效。