基于差分隐私保护技术的多方求和查询方法

何贤芒

基于差分隐私保护技术的多方求和查询方法

何贤芒

（东莞理工学院网络空间安全学院，广东 东莞 623808）

差分隐私保护技术因其不需要攻击者先验知识的假设，而被认为是一种非常可靠的保护机制。然而，差分隐私保护技术很少在多方环境下使用。鉴于此，将差分隐私保护技术用于多方环境下数据求和查询问题，详细讨论了如何通过加入噪声的方法来实现数据的保护，并证明该方法安全性。

多方求和；隐私保护；差分隐私；数据查询

1 引言

网络技术的飞速发展，促使信息量正以超乎人们想象的速度增长。不同的组织间或个人间的合作计算变得越来越重要。不同的数据拥有者需要通过合作交流计算信息得到更全面、更有价值的计算结果。然而，数据安全与隐私保护问题制约着合作计算的进行，甚至在某些情形下参与各方不得不舍弃合作来确保数据的私有与安全。在商业应用上，多个商家的竞争关系往往为了决策需要合作进行数据挖掘来了解整个市场的情况。例如，不同的手机运营商需要通过合作计算来了解某个地区某些手机品牌的使用情况。各个商家拥有的数据是商家的私有信息，不希望对方知道，也可能商家拥有的数据不宜对外公开（如使用者的通话记录）。在这种情况下，需要多方在合作进行数据挖掘的同时保证各方的私有数据不被泄露。为解决该问题，越来越多的学者将努力方向聚焦在安全多方计算（SMC，secure multi-party computation）[1-2]的研究中，研究与设计在多方参与不泄露各方私有信息的条件下完成合作计算。安全多方计算使不公开私有信息的合作计算成为可能，其研究促进了各个组织或个人之间的信息流通并且在各个领域拥有广阔的应用前景。目前，安全多方计算研究已经取得了较大的进展，并且日益成为现代密码学的重要研究课题。

然而，由于基础理论研究的复杂性和应用问题的多样性，基于传统的安全多方计算协议设计过于复杂，不易操作。差分隐私保护是一种数据失真的隐私保护技术，采用添加噪声的技术使敏感数据失真但同时保持某些数据或数据属性不变，要求保证处理后的数据仍然可以保持某些统计方面的性质，以便进行数据挖掘等操作。本文拟将其应用在多方环境下数据求和查询问题，在保持查询结果精确性的前提下同时保证其安全性。

2 差分隐私保护技术

差分隐私保护技术建立在坚实的数学基础之上，对隐私保护进行了严格的定义并提供了量化评估方法，使不同参数处理下的数据集所提供的隐私保护水平具有可比较性。因此，差分隐私理论迅速被业界认可。

定义1 差分隐私[3-4]。一个随机算法满足-差分隐私保护，当且仅当对于任何相差仅一个元组的两个集合1、2和任何输出，满足如下条件

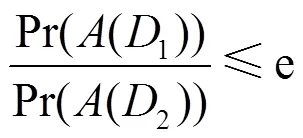
这里的是使用者指定的常数，1和2至多相差一个元组，e是自然对数常数。从数学上看，只要这个参数足够小，攻击者很难区分出对同样的输出，查询函数到底是作用在1还是在2上。当参数等于0时，输出的仅是噪声才能满足上述要求，所以参数只有大于0才有实际的意义。同样条件下，参数越小私密性越好。

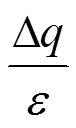
定义2 敏感度。Δ是查询函数的敏感度,其定义如下。

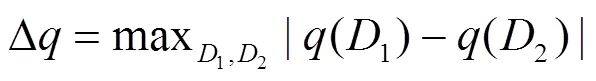
数据集1和2之间至多相差一个元素。

3 目前方案

多方安全求和协议是一类重要基础的协议。目前已经有一系列文献[5-14]对安全求和协议进行了研究。这些方法各有优劣。文献[5]提出从多个参与者中选择一个主站点，让其产生一个随机数加上自己的数据发给下一个参与者，后面的参与者加上自己的真实数据依次传下去，最终传回主站点再减去随机数之后进行广播。此方法通信性能好，但安全性太差，相邻的两个参与者共谋便可得到中间参与者的数据。

为了解决合谋问题，文献[6]将每位参与者自己输入的数据随机划分成份，然后每位参与者把分成的份分别发给所有的参与者，每位参与者分别计算自己收集到的数据的和，然后广播给其他参与者，最后每位用户再次分别计算自己收集到的数据，计算出总和。这种算法固然相对于文献[5]安全很多，但其通信需要2次，通信复杂度较高。文献[7]提出基于博弈论的安全多方求和协议，主要考虑了用户不诚实提供数据的情况，每个用户数据分成份，每次计算做-轮迭代，做二次前后结果是一致的，发布求和结果，如果不一致，则说明有站点提供不真实数据，主站点重新发起求和运算，直到连续两次运算得到的和一样。文献[8]为了解决通信度高的问题，采用了公钥加密与随机函数，提出了一种能提高安全性又能降低通信复杂度的协议。张恩等[9]结合博弈论和密码算法, 提出了一种基于电路计算的理性安全多方求和协议。Mehnaz等[10]提出了一种基于诚实模型的安全求和协议, 并且应用在机器学习中。Ashouri-Talouki等[11]提出了无须安全信道的3个安全求和协议。仲红[12]提出了基于安全多方求和的多候选人电子选举方案。文献[13]讨论了在通用可组合框架下研究安全多方计算的公平性问题。Liu等[14]提出了一种基于双粒子Bell 态的量子安全多方求和协议。Jung等[15]提出了一种没有安全通信信道或没有可信密钥分发者的安全求和协议。

4 多方环境下求和协议

目前为止，差分隐私保护技术难以做到准确的数据查询，而本文可以用差分隐私这种方法实现在多方参与情况下数据准确求和查询，本文的安全性是基于差分隐私保护这种机制，具有安全性保证；从查询速度来说，与目前的其他数据交换方法相同，因此通信量是一致的。

本节提出一个在多方环境下的数据库统计查询方法，设参与方的数量至少是3，显而易见，当=2时，求和查询是无法做到数据安全的，步骤如下。

例1演示了上述求和全过程，定理1证明上述方法满足隐私保护技术的要求。

定理1 上述多方求和计算方法满足max{ε}-差分隐私。

证明 设1,2是任意两个兄弟集合，仅差一个数据元组，是算法2的一个输出，是算法1可能输出集合。

情形11，2算法输出是离散类型

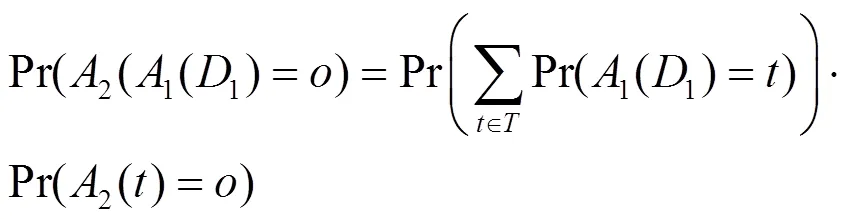
根据定义1

由上面的式子可以得出

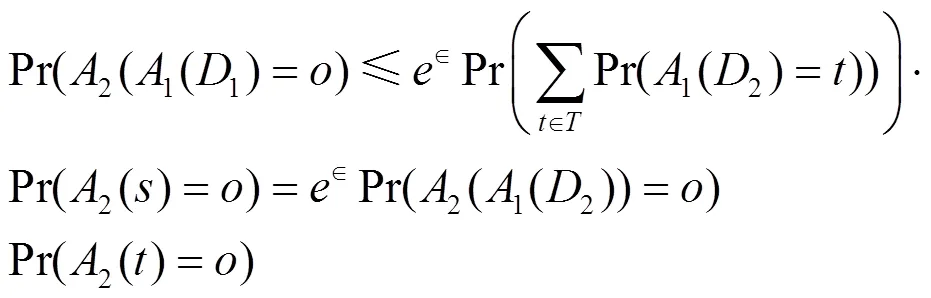
情形21，2算法输出是连续类型

类似地有

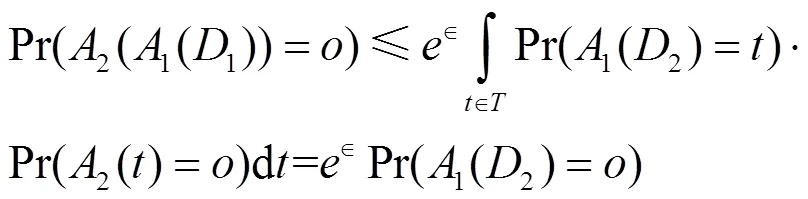
上述的证明表明任意参与方P，在其拥有的值x基础上增减多个满足拉普拉斯分布的数x，其依然满足max{ε}-差分隐私的要求。

从过程来说，这个协议通信次数需要(2)。结合博弈论等方法，通信量可以降低到()，≥2是可能合谋的参与方的数量。在通信量降低的同时，其安全性依然满足定理1的要求。

从协议的执行过程来看，参数的选择与求和查询结果无关，只跟加入的噪声大小有关。考虑到噪声的加入最后全部抵消，因此，定理2是显而易见的，参数的选择不影响查询结果。

定理2 参数的选择对求和结果没有影响。

步骤3 如图1所示，进行数据交换，具体如下。

图1 数据交换示例

Fig 1 Example of data exchange

1=3−(3.5+121.2−129.2)+(−2.5−21.4−12.3) =−28.7

2=4−(−2.5+87.5−12.5)+(3.5+176.4+20.4)=131.8

3=6−(−21.4+176.4+44.5)+(121.2+ 87.5+78.6)=93.8

4=7−(−12.3+20.4+78.6)+(−129.2−12.5+44.5)=−176.9

步骤5 计算1+2+3+4=20，即总和。

根据定理1，上述的多方求和计算方法满足0.01-差分隐私保护技术。

5 结束语

虽然差分隐私保护技术得到了学者的广泛关注，但如何在实际中、在多方环境下应用差分隐私保护技术依然是个开放问题。鉴于此，本文提出了一个基于差分隐私保护模型多方环境下求和查询方法，下一步将其推广到MAX与MIN查询，并且在这个方面取得进展。

[1] BARVE R, SHRIVER E, GIBBONS P B. Modeling and optimizing I/O throughput of multiple disks on a bus[J]. ACM Sigmetrics Performance Evaluation Review, 1999, 27(1): 83-92.

[2] LU Y P, DAVID H C D. Performance study of ISCSI-based storage subsystems[J]. IEEE Communications Magazine, 2003, 41(8): 76-82.

[3] DWORK C. Differential privacy[C]//International Colloquium on Automata, Languages, & Programming. 2006: 1-12

[4] PROSERPIO D, GOLDBERG S, MCSHERRY F. Calibrating data to sensitivity in private data analysis[C]//The Third Conference on Theory of Cryptography. 2006: 265-284

[5] CLIFTON C, KANTARCIOGLU M, VAIDYA J, et al. Tools for privacy preserving distributed data mining [J]. Sigkdd Explorations, 2002, 4(2): 28-34.

[6] 罗永龙, 徐致云, 黄刘生. 安全多方的统计分析问题及其应用[J]. 计算机工程与应用, 2005, 41(24): 141-143.

LUO Y L, XU Z Y, HUANG L S. Multivariate statistical analysis and its application[J]. Computer Engineering and Applications, 2005, 41 (24): 141-143.

[7] 张国荣, 印鉴. 基于博弈论的安全多方求和方法[J]. 计算机应用研究, 2009, 26(4): 1497-1499.

ZHANG G R, YIN J. Multi-party secure sum computation based on game theory[J]. Journal of Computer Applications, 2009, 26 (4): 1497-1499.

[8] 王峥, 郝林, 刘义成. 基于公钥加密的安全多方求和协议[J]. 计算机应用研究, 2017(4):179-182.

WANG Z, HAO L, LIU Y C. Secure sum protocol based on public key encryption [J]. Journal of Computer Applications, 2017 (4): 179-182.

[9] 张恩, 朱君哲, 范海菊, 等. 基于电路计算的理性安全多方求和协议[J]. 密码学报, 2019, 6(1): 126-135.

ZHANG E, ZHU J Z, FAN H J, et al. Rational secure multiparty sum protocol based on circuit computing [J]. Chinese Journal of Cryptography, 2019, 6 (1): 126-135.

[10] MEHNAZ S, BELLALA G, BERTINO E. A secure sum protocol and its application to privacy-preserving multiparty analytics[C]//The 22nd ACM on Symposium on Access Control Models and Technologies. 2017: 219-230.

[11] ASHOURI-TALOUKI M, BARAANI-DASTJERDI A. Cryptographic collusion-resistant protocols for secure sum[J]. International Journal of Electronic Security and Digital Forensics, 2017, 9(1): 19-34.

[12] 仲红, 黄刘生, 罗永龙. 基于安全多方求和的多候选人电子选举方案[J]. 计算机研究与发展, 2006, 43(8): 1405-1410. ZHONG H, HUANG L S, LUO Y L. A multi-candidate electronic voting scheme based on secure sum protocol[J]. Journal of Computer Research and Development, 2006, 43(8): 1405-1410.

[13] 田有亮, 彭长根, 马建峰, 等. 通用可组合公平安全多方计算协议[J]. 通信学报, 2014(2):54-62.

TIAN Y L, PENG C G, MA J F, et al. Universally composable secure multiparty computation protocol with fairness[J]. Jounral on Communications, 2014(2): 54-62.

[14] LIU W, WANG Y B, FAN W Q. An novel protocol for the quantum secure multi-party summation based on two-particle bell states[J]. International Journal of Theoretical Physics, 2017, 56(9): 2783-2791.

[15] JUNG T, LI X Y, WAN M. Collusion-tolerable privacy-preserving sum and product calculation without secure channel[J]. IEEE Transactions on Dependable and Secure Computing, 2015, 12(1): 45–57.

Multi-party summation query method based on differential privacy

HE Xianmang

School of Cyberspace Science, Dongguan University of Technology, Dongguan 623808, China

Differential privacy is considered to be a very reliable protection mechanism because it does not require the a prior knowledge for the attacker. However, differential privacy is rarely used in a multi-party environment. In view of this, the differential privacy is applied to the data summation query in multi-party environment. This method was described in detail and proved the security of the method.

multi-party summation, privacy preservation, differential privacy, data query

TP301

A

10.11959/j.issn.2096−109x.2020032

2019−10−08；

2020−02−22

何贤芒，x.m.he@163.com

国家自然科学基金（61672303）；广东省普通高校特色创新项目（2018KTSCX221）

The National Natural Science Foundation of China (61672303), Characteristic Innovation Projects of Universities in Guangdong Province, China (2018KTSCX221)

何贤芒. 基于差分隐私保护技术的多方求和查询方法[J]. 网络与信息安全学报, 2020, 6(3): 14-18.

HE X M. Multi-party summation query method based on differential privacy[J]. Chinese Journal of Network and Information Security, 2020, 6(3): 14-18.

何贤芒（1981− ），男，浙江三门人，东莞理工学院副教授，主要研究方向为数据安全与隐私保护。