水轮机蝴蝶阀蝶板截面多目标优化设计

牛萌萌，李宪华

(1.安徽粮食工程职业学院 机电工程系，安徽 合肥 230001；2.安徽理工大学 机械工程学院，安徽 淮南 232000)

水轮机蝴蝶阀通常用于阀门所需压降较低的应用中，其主要功能是控制流量或压力的开启与关闭。蝶板通过一根阀轴定位在中心，阀轴使蝶板平行于或垂直于液流，并且阀轴连接到阀门外部的手柄或其他操作器和结构。与球阀不同，蝶板始终存在于流场中，因此无论蝶板位置如何，压降始终存在。由于蝴蝶阀对流经它的液流影响显著，因此各国学者对蝴蝶阀进行了大量研究。早在1995年，小川和木村[1]研究了阀门扭矩特性和蝶板引起的压降。JANUSZ和CZESLAW[2]通过使用实验和数值结合的方法研究了一种常用的蝴蝶阀，该阀具有薄而平的尖锐蝶板且堵塞比d/D为0.947。洪宇[3]通过对水轮机进水蝶阀进行仿真分析，对水轮机进水蝶阀的结构进行优化，提高其工作性能和可靠性。郭建章等[4]基于Fluent软件提供的湍流模型与离散相模型,对中线蝶阀内部流场进行了数值模拟研究,考察了阀门开度对蝶阀壁面及蝶板磨损的影响。张融等[5]利用ANSYS Work Bench对其结构强度及抗震能力进行了仿真分析并对阀轴进行结构优化改进。以上这类研究主要集中在蝴蝶阀的流体分析或者整体结构分析上，而不是聚焦在蝶板形状上。因此，本文提出了一种兼顾流动特性和结构安全性的蝴蝶阀蝶板多目标优化设计。

研究的过程包括三个部分。首先，依据阀门中的压力损失系数和最大应力进行拓扑优化以识别蝴蝶蝶板的截面形状。其次，采用正交阵列和逐步回归响应面法建立压力损失系数和最大应力的替代模型。最后采用权衡方法，实现多目标优化及设计变量优化。

1 试验方法与设计

在本研究中，设计条件要求该蝶阀既具有较小的压力损失系数(k≤0.8)，又具有足够的结构系数(SF≥1.5)以用于特殊用途。这些关键因素并未根据用户的要求进行考虑。根据期望，蝶板的直径和最大厚度分别定义为100 mm和20 mm。

1.1 正交实验和替代模型

替代模型方法使用一些基本函数来近似设计问题中涉及的高度复杂的目标和约束函数[6]。替代模型的主要步骤通常包括选择实验设计以生成采样数据；选择模型代表数据；最佳地将模型拟合到采样数据这三个步骤，其中的每一个都有多种选择，并且每个步骤都有一些优点和缺点。发现没有最佳的单一替代模型可用来适应所有工程问题。在这项工作中，选择正交阵列作为实验组，采用逐步回归的响应面法作为仿真试验设计。

根据阀门中的压力损失系数和最大应力进行拓扑优化，选择影响蝶板截面形状的七个设计变量，它们显示在图1的中间半径R，臂长L1和L2，蝶板边缘的厚度T1和T2以及中间厚度W1和W2。

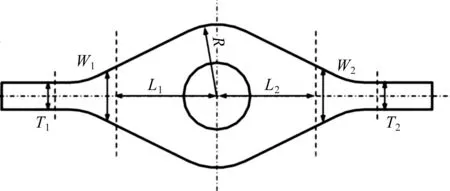
图1 蝶板截面主要形状变量

通常，以上变量需要使用全因子设计进行36次的分析。但是，通过使用L18(21×37)正交排列组合的阵列，实验组数可以减少到18[7]。

1.2 优化方案

本文利用拓扑优化和尺寸优化来获得性能更好的蝴蝶阀蝶板。尺寸优化在拓扑优化的基础上确定蝴蝶阀的详细形状。本研究有两个需要优化的目标，一个是压力损失系数，另一个是作用在蝶板上的应力。多目标优化是同时优化两个或两个以上受某些约束冲突的目标的过程。一般的多目标优化表示为：

minF(x)=[f1(x),f2(x)，...，fk(x)]
s.t.gi(x)≤0，i=1,2,...,I
hj(x)≤0，j=1,2,...,J
x∈S

(1)

其中，f1(x),f2(x),...,fk(x)是k的目标函数；g(x)和h(x)分别是不等式约束，x=(x1,x2,...,xn)T是n个设计变量，x∈S定义设计空间。

为了进行多目标优化，本研究采用权衡方法。该方法允许设计人员按照重要性从1到k降序对目标进行排列。然后，每个目标函数都会受到最小化的约束，该约束不允许新函数的最小值超过先前函数的最小值的规定分数[8-9]。一旦从f1(x)(最重要)到fk(x)(最不重要)对k个目标进行了排序，则求解过程如下：

步骤1：假定不存在所有其他目标函数，则在原始约束集的约束下找到f1(x)及其对应变量x1的最佳点。

步骤2：定义一个值为εj，然后在附加约束条件下找到第j个目标函数fj(x)的最优点：

(2)

其中εj是假设的函数增量系数，%。

2 实验结果与分析

2.1 拓扑优化

图2给出了蝴蝶阀蝶板截面的有限元模型，用于拓扑优化。该模型的材料是STS316，其杨氏模量E=193 GPa、泊松比v=0.27。黑色区域表示无法删除的元素，浅灰色区域表示可以在拓扑优化中将其删除。在各个方向上带有箭头的短线表示已知实验数据分析获得的各种流体压力。应该注意的是，在阀门下游也有压力，但是下游作用在蝶板表面上的压力与上游表面上的压力相比太小，因此可以忽略。

图2 二维蝴蝶阀蝶板的有限元模型

图3显示了拓扑优化结果的重量减少40%。圆圈D中浅灰色区域可以删除，对整体配置影响不大。也就是说，蝶板的周边可以做得很薄。

图3 拓扑优化

根据拓扑优化的结果，新模型(见图4)。相应的流场分析在相同的边界条件下进行应力分析。标记为“MX”的最大应力为50.5 MPa，出现在拐角区域，这表明流动的流体在前场相反的一半上产生更高的阻力。由于STS316的屈服应力为205 MPa，因此该新模型的安全系数大于4.0(K1=1.577 9)，表明可以引用此模型以作为原型，下一步将基于该原型进行尺寸优化。

图4 拓扑优化后的新有限元模型及其应力分布

2.2 逐步回归的响应面法

获得实验结果后，在线性函数中构建压力损失系数的替代模型，并在二次函数中构建应力的替代模型，如下所示[10]：

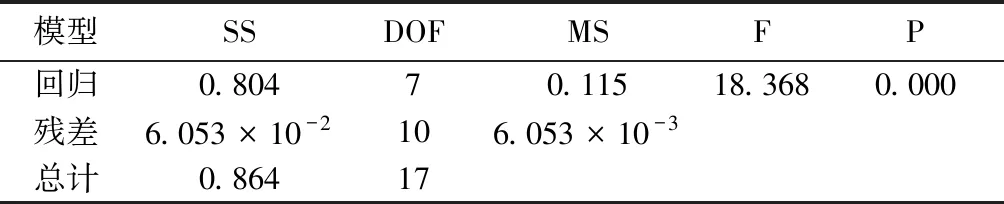
K1=0.28+(-9.6R-4L2-3L1-2.7W2-3.3W1+9.8T2-0.2T1)×10-2

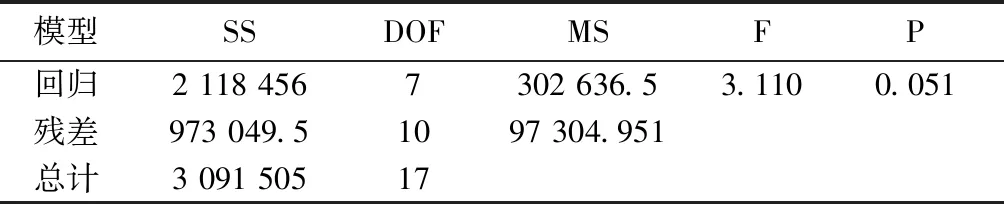
表2 拟合σmax模型的方差分析

2.3 权衡方法的多目标优化

如上所述，本研究的设计目标是最小压力损失系数以及最大应力。因此，目标和约束函数可以定义如下：

minF(X)={K1,σmax}
s.t.σmax≤136.7 MPa(安全系数=1.5)
K1≤0.8
1≤x≤3

其中x=[R,L1,L2,W1,W2,T1,T2]T，数字“1”和“3”分别代表下限和上限。

基于这两个替代模型，使用权衡方法求解多目标优化。此方法将目标按重要性降序排列。然后，每个目标函数都会受到最小化的约束，该约束不允许新函数的最小值超过先前函数的最小值的规定分数。在本研究中，解决方法如下：

步骤1：

minF(X)=σmax
s.t.σmax≤136.7 MPa
K1≤0.8
1≤x≤3 (X=[R,L1,L2,W1,W2,T1,T2]T)

下一步是找到第二个目标函数的最优值，它受一个附加约束。

步骤2：

minF(X)=K1
s.t.σmax≤136.7+1.305 MPa
K1≤0.8
1≤x≤3 (X=[R,L1,L2,W1,W2,T1,T2]T)

经过上述两步解决方法，可以获得最佳解决方案和最优结果(见表3)。x的最优水平(不是实际尺寸)在表4可以发现，T1、W1、L1的尺寸分别接近其上限。相反，T2、W2、W2的尺寸分别接近其下限。

表3 最优结果

表4 设计变量的最优结果

3 结论

本文提出了在多目标优化下水轮机蝴蝶阀蝶板设计过程。该过程根据初始设计给出压力损失系数，确定阀门行业中常用的系数,采用有限元方法进行拓扑优化，得到基本形状,然后采用正交阵列和逐步回归响应面法建立压力损失系数和最大应力的替代模型。最后采用权衡方法，根据公式直接求得多目标的变量最优解。权衡方法与响应面模型相结合，可以准确并有效地预测最佳条件。

需要注意的是，本文仅对蝶板的截面进行了优化，采用的是二维有限元模型。将来的文章中应考虑包括蝶板、流体在内的三维有限元分析。