嵌套型遗传算法的海水淡化系统优化调度研究
时国平,翟龙华,钱叶册
(池州学院,安徽 池州 247000)
随着工业技术的进一步推进,工业污染和废弃物的不合理排放问题也日益凸出,导致淡水资源严重短缺。海水淡化技术是解决该问题的重要技术之一,其产出的淡水产量已达全世界淡水总产量的44%。而如何在机组设备正常运行并满足用户用水需求的条件下对其进行优化调度,使系统高效、节能地运行是一个值得研究的问题。
文献[1]建立了单目标规划模型,并采用分支定界法、遗传算法等方法对模型进行求解与比较,并开发了反渗透海水淡化优化调度信息系统。海水淡化系统优化调度能有效地降低制水成本,达到节能的目的。文献[2]在海水淡化研究过程中,以操作费用最小为目标函数,以开放方程描述的各模型方程为约束,以设备和产品质量限制为边界条件,采用联立求解技术将微分代数方程组成的优化问题转化成大规模非线性规划问题进行优化求解。文献[3-4]主要研究需求不确定环境下的反渗透海水淡化工程的调度问题,在考虑鲁棒性的情况下建立系统优化调度的期望值模型,该模型根据约束中随机参数的概率分布,构造了新的鲁棒性约束,改进了原有的期望值模型,使解空间收缩,满足一定的鲁棒性要求。文献[5]首先建立反渗透海水淡化系统的经济模型,针对模型提出一种求解非线性约束优化问题的改进差分进化算法。该算法对基本差分进化算法中的变异因子和交叉因子进行改进,避免了早熟收敛,提高了算法的寻优能力;基于差分算法的反渗透海水淡化优化调度。文献[6-8]提出了一种随机优化框架,将调度分为鲁棒预调度、反应式重调度。鲁棒预调度在一定的置信区间上满足了用水量需求,反应式重调度在提高经济性的同时也减少了对原生产调度计划的影响,采用最优化遗传算法中最小二乘法来求解诊断方程,能够快速有效的搜索复杂、多维以及非线性空间,大大提高工作效率,减小操作量[9-11]。
以上这些研究大多是基于确定数量蓄水池与机组配置基础上的投切优化,而没有考虑海水淡化设备的优化配置。因此,本文建立多目标规划模型,考虑可行的最小设备配置,并在此基础上进行调度优化。
1 海水淡化系统优化调度模型
1.1 目标函数
(1)优化各蓄水池总容量COL
(1)
式中,Ni表示0-1变量,是否需要第i台蓄水池;Gmax,i—第i台候选蓄水池的最大容量。如图1所示,两台机组与一台蓄水池相连的形式是海水淡化装置的基本配置,若干个蓄水池组成海水淡化装置体系。蓄水池有不同的容量规格,大容量的蓄水池与大功率的淡化机组相连,反之亦然。因此,对各蓄水池总容量的优化不仅仅是对所需蓄水池数量的优化,同时也能得到不同规格蓄水池的最佳组合[12]。

图1 机组与蓄水池的基本配置图
(2)优化第k个时间段总供水量Qk
在满足约束条件中第k个时间段总供水量Qk大于该时间段预测需水量PQk的条件下,最小化Qk的值,这样一方面能够减轻机组的负荷量,另一方面可以防止机组产水量过多导致蓄水池溢出[13]。
(3)优化运行费用E
运行费用可分为能耗费用E1以及维护费用E2两部分,其计算方法按式(2—3)所示。
E1=ekC3Qi,j,k
(2)
(3)
其中,Qi,j,k—第i台蓄水池第j台机组k时刻产水量;Mi,j,k—0-1变量,第i台蓄水池第j台机组k时是否开启;C1—运行时机组维护保养费用G=0.15;C2—停机时机组维护保养费用C2=55;C3—能耗与制水量关联系数,C3=2.86。
1.2 约束条件
(1)总供水量约束
第k个时间段各机组的供水量之和应大于该时间段内的需求供水量。
(4)
式中,PQk表示第k时刻预测需水量。
(2)机组供水量约束
第k个时间段内各机组的产水量应在其供水能力的上下限内。
Qmin,i,j≤Qi,j,k≤Qmax,i,j
(5)
式中,Qmin,i,j—第i台蓄水池第j台机组产水量下限;Qmax,i,j—第i台蓄水池第j台机组产水量上限。
(3)机组启停约束
一个周期内机组启停次数应小于最大阈值。
(6)
式中,Nsmax表示机组启停次数上限。
机组连续运行时间约束
(7)
式中,Nrmax表示机组连续运行时间上限。
1.3 模型
将最小化各时刻总供水量目标转化为约束,即引入系数α,总供水量约束如式(8)所述。
(8)
综上,双目标规划模型如公式(9)所示,决策变量为各蓄水池组合向量N、各机组启停向量M以及各机组供水量向量Q。
minCOL
minE
(9)
2 遗传算法及仿真结果
将规划模型分解为多个子问题,并用多层遗传算法分别对其进行求解,采用嵌套型的遗传算法对各决策变量进行串行搜索,以克服决策变量过多导致单层遗传算法无法寻得可行解的问题。其中内层遗传算法1主要对机组启停向量进行搜素;内层遗传算法2是在可行解的基础上对决策变量进行搜索;外层遗传算法是采用二进制编码,对蓄水池组合进行随机搜索。算法流程图(见图2)。
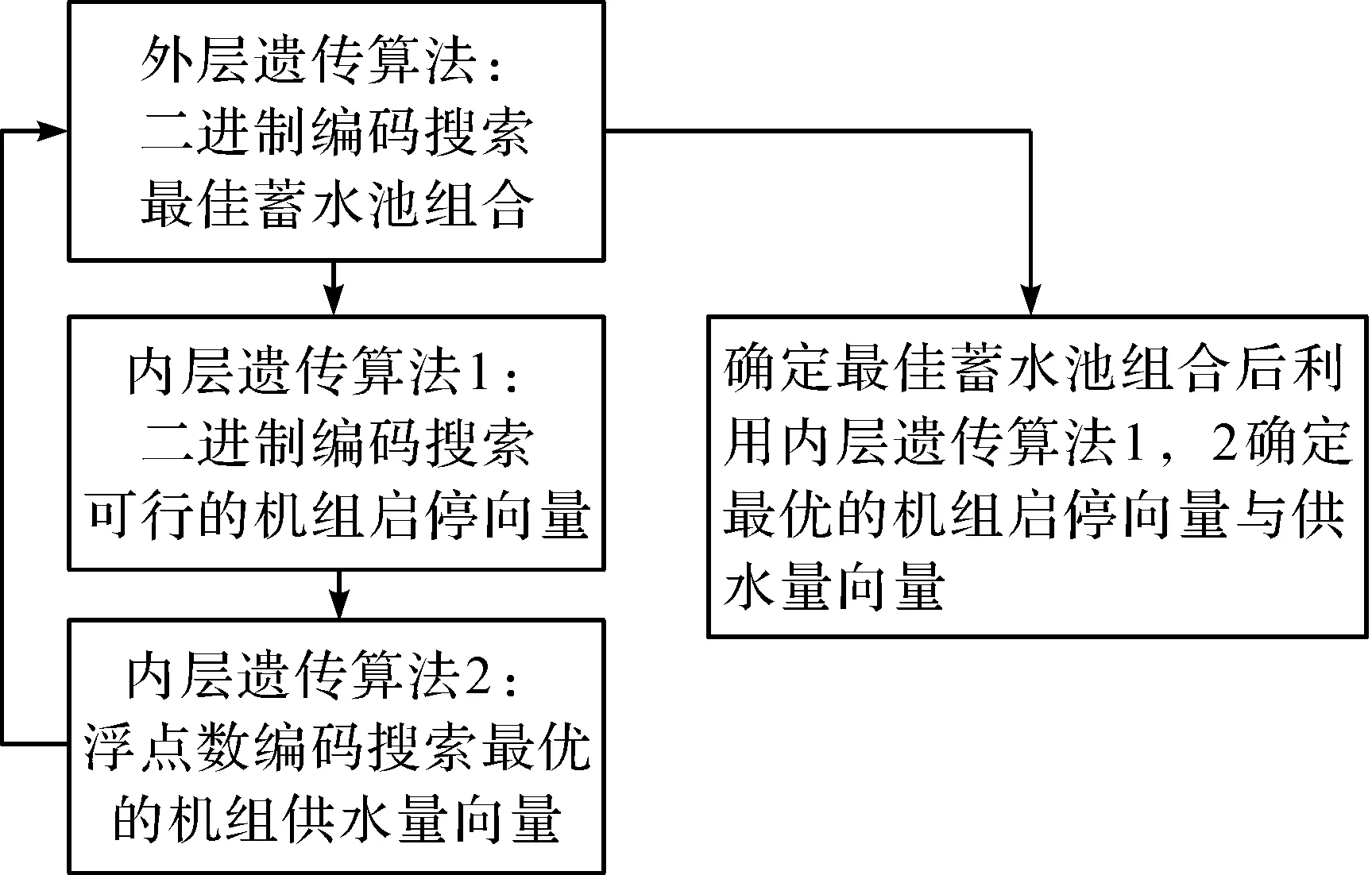
图2 搜索算法流程图
以下对表1所示三类蓄水池算例进行仿真求解,每类各5台作为候选。一天不同时段的电价(见表2)。表3为预测的一天每小时需电量。每台蓄水池分配两台机组,一天作为一个周期,分为24个时刻。系数α取1.1,每台机组启停次数上限Nrmax取16,每台机组最大连续运行时间Nrmax取12。

表1 蓄水池规格

表2 电价表

表3 各时刻预测需电量
2.1 蓄水池组合N的优化
2.1.1 内层遗传算法1
本层遗传算法主要对机组启停向量M进行搜素。对于向量M,除机组启停约束以及连续运行时间约束外,还需满足每个时刻内预测需水量在各机组最大供水量之和与最小供水量之和之间,否则必定不满足约束,子模型如公式(10)所示[14]。
本层遗传算法采用二进制编码,一个染色体即对应一个M向量,采用轮盘赌,单点交叉以及单点位变异的方式进行随机搜索。利用惩罚函数法对不满足约束条件的个体进行惩罚,惩罚因子由公式(11—13)定义,适应度函数如公式(14)。
(10)
(11)
(12)
(13)
(14)
因此,当个体适应度达到1 h,各惩罚项均为0,该个体为可行解。遗传算法搜索结果(见图3),即已搜索到可行解。
2.1.2 内层遗传算法2
内层遗传算法2在可行解M的基础上对决策变量Q进行搜索,子模型如公式(15)所示,即在满足总供水量约束与机组供水量约束的条件下最小化运行费用。
该层遗传算法采用浮点数编码,将染色体的每一位值限制在该位对应机组的供水上下限内,即满足机组供水量约束条件。而对于总供水量约束仍利用罚函数法进行惩罚,惩罚因子计算如公式(16)所示,而运行费用E的计算已由公式(2—3)给出。适应度函数定义如公式(17)所示[15]。
minE
(15)
(16)
(17)
如图4所示,该次搜索最佳适应度为1.25,即能耗费用为80 063元,且满足约束条件。
2.1.3 外层遗传算法
该层遗传算法是对蓄水池组合N的随机搜索,采用二进制编码。例如对于15台待选的蓄水池,染色体[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1]表示只选用第一与最后一台(容量从小到大排列)。选定组合后输入内层遗传算法进行搜索,若未搜索到可行解则其适应度为0,否则按公式(18)计算,即选中的蓄水池容量和越大,适应度越低。
(18)
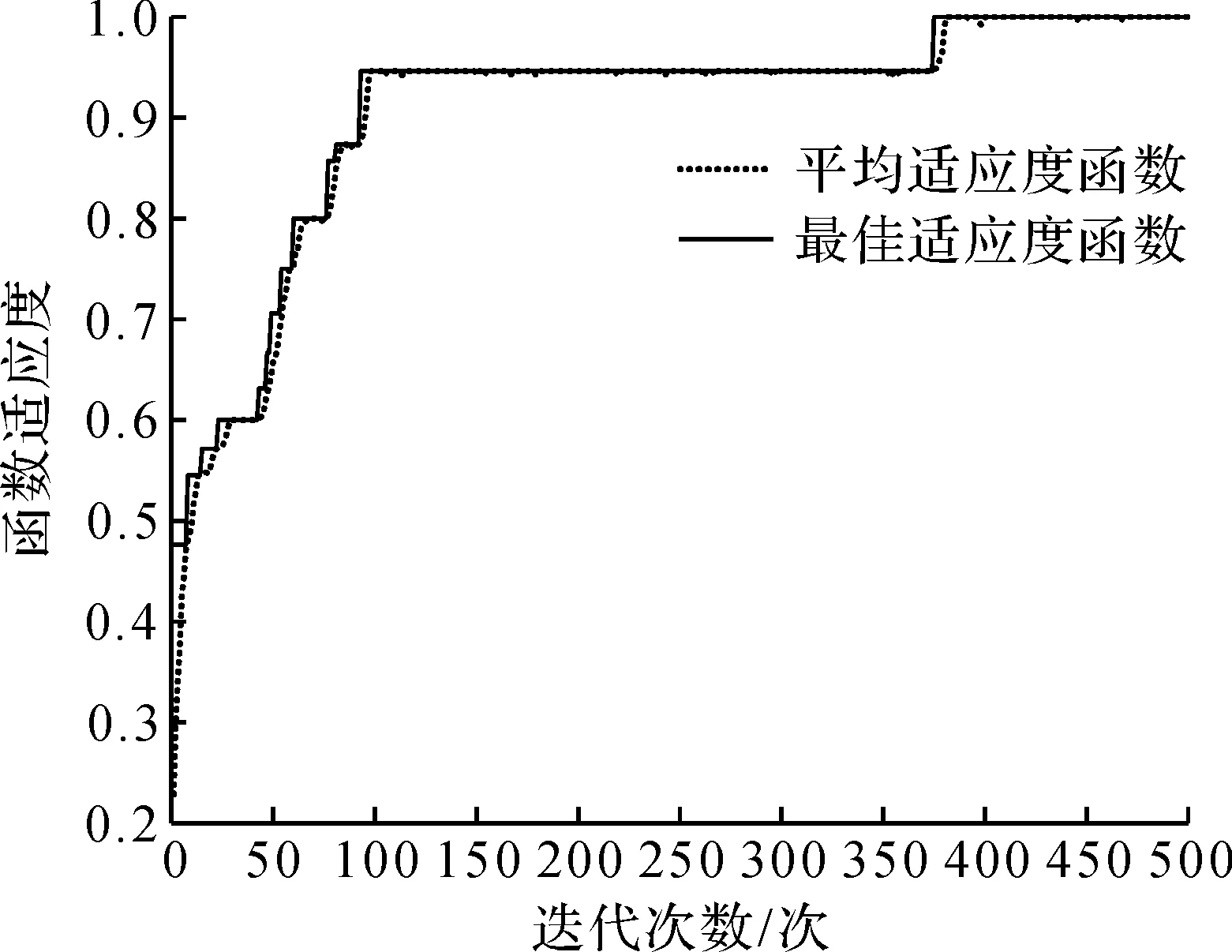
图3 内层遗传算法1进化曲线

图4 内层遗传算法2进化曲线
寻优结果(见图5),最佳染色体为[0 0 0 1 1 0 0 1 0 1 0 0 0 1 0],即两台1 280容量的蓄水池,两台1 680容量的蓄水池以及一台2 280容量的蓄水池。
2.2 机组启停向量M以及供水向量Q的优化
在确定最优的蓄水池组合N之后,再利用内层遗传算法1以及内层遗传算法2对M以及Q进行进一步优化。即多次(本次实验取50次)产生可行的启停向量M,并搜索最优供水向量Q,并记录最优值。
图6—7分别为50次实验的运行费用分布图以及最优情况变化曲线。最低能耗费用为80 063元。
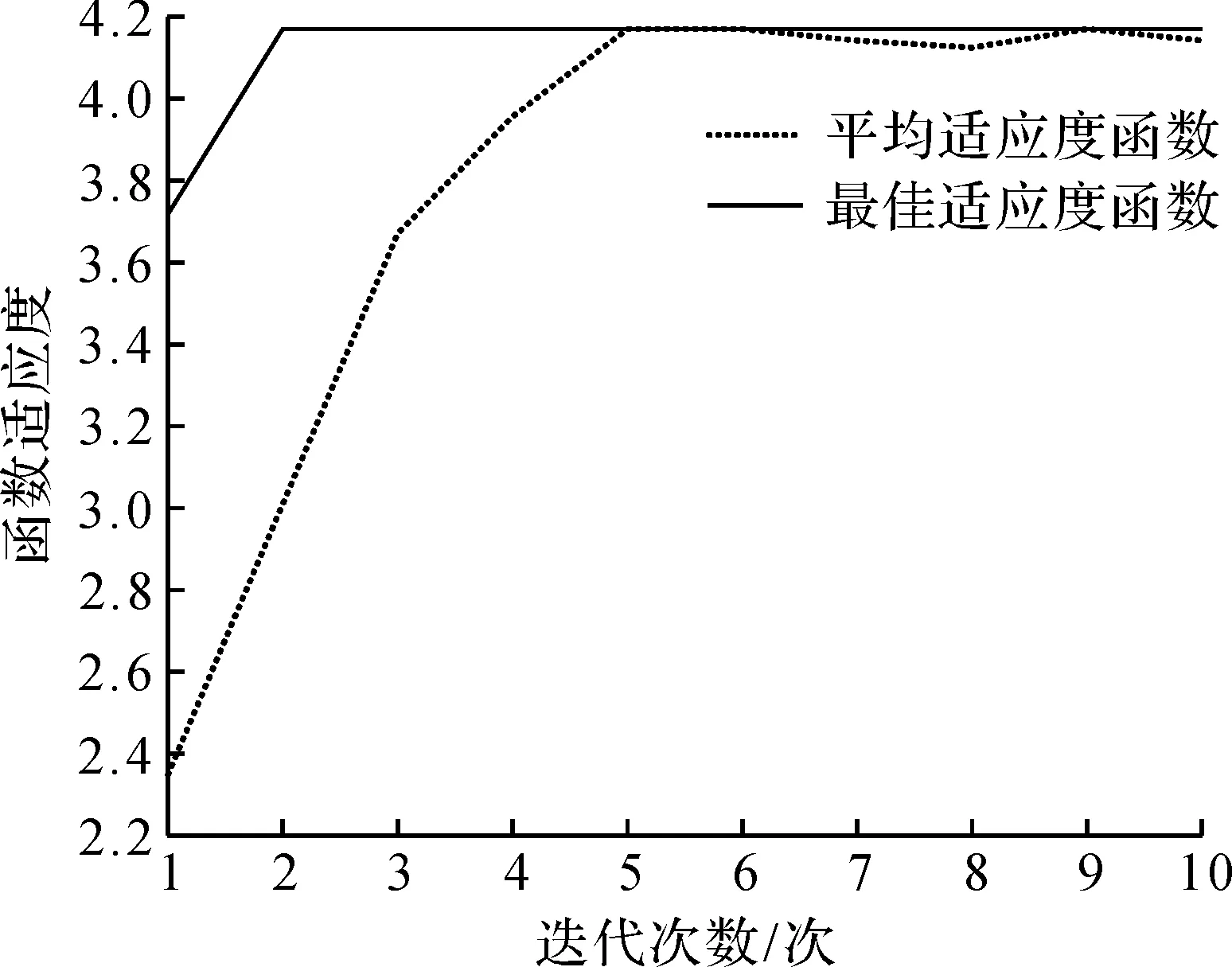
图5 外层遗传算法进化曲线

图6 运行费用分布图

图7 最优情况变化曲线
仿真结果表明,基于嵌套性遗传算法具有高效的全局搜索能力,避免了单次遗传算法有限的搜索能力,无法很好的同时对0-1向量M以及实数向量Q进行搜索,需要分别对这两个决策向量进行分步搜素。合理设置参数约束范围及适应度函数,可以快速计算出调度方案的优化结果。
3 结论
本文提出了一种多目标的海水淡化系统优化调度研究策略,采用嵌套型遗传算法进行求解。通过理论分析和仿真验证,本文研究得到如下结论:
(1)考虑海水淡化设备的优化配置,建立多目标规划模型,考虑可行的最小设备配置,并在此基础上进行调度优化。可实现对各蓄水池总容量、各个时间段总供水量以及运行费用降到最低要求。
(2)利用嵌套型遗传算法进行求解,分别对蓄水池组合、机组启停向量以及供水向量三组决策变量进行分步串行搜素,有效增强算法的搜索能力,找到可行的最优解。

