基于SFSO算法的多变量PID控制器设计

李闯勤

（航空工业飞机强度研究所，陕西 西安 710065）

在工业过程控制系统中，蒸馏塔作为一类复杂的控制对象，其输入输出间存在强耦合特性。由于其具有多个输入和多个输出，因此要实现对多变量过程控制对象的最优化控制就比较复杂。多变量过程系统的控制器设计，虽然采用多变量PID控制器，但是在多变量PID控制器的设计过程中，需要解决PID参数的优化与整定问题，以使系统达到控制最优。

基于社会力模型的群体智能优化算法SFSO（Swarm Optimization algorithm based on Social Force model）是阎高伟等人提出的一种群体智能优化算法[1，2]。本文将智能优化算法SFSO应用于蒸馏塔多变量PID控制器参数整定，并进行了研究与分析。

1  SFSO算法

社会力模型作为一种多个体自驱动系统，模型中的个体具有思考和对周围环境做出反应的能力，把人的主观愿望、个体之间的相互关系以及人与环境之间的相互影响有机联系起来。SFSO算法结合社会力模型、行人的决策行为以及个体间协作等行为，实现了对决策空间的搜索。在SFSO算法中，行人向目标运动的方向代表算法的搜索进化方向。算法在搜索过程中一旦陷入局部最优解，依靠行人间排斥力，使个体搜索路径发生变化，避免算法陷入局部最优[1]。

SFSO算法具有如下特点：（1）在求解多模态函数时能够并行对多个全局最优解进行搜索，并最终收敛到多个全局最优解；（2）算法的这种搜索机制能够使种群的多样性保持在一个较好的水平，防止算法过早陷入局部最优；（3）SFSO算法的搜索机制使算法在处理不同类型的优化问题时，具有很强的鲁棒性。

SFSO算法主要包括以下几个阶段：初始化、群体分类阶段、社会力驱动阶段和协作阶段[2]。

1.1  初始化

初始化阶段主要完成：（1）种群数量N、搜索代数Itermax等相关参数的设定。行人的初始速度、历史记忆、社会力初始化时均设置为零向量；（2）产生初始行人群体。行人α的当前位置 按照公式进行初始化。

1.2 群体分类阶段

在向目标运动的过程中，行人会根据自己当前位置到目标的距离而选择成为自由个体还是非自由个体。子群体Gk中的行人α成为自由个体的概率，按照如下步骤计算：（1）对Gk中的所有行人个体当前位置到目标的距离进行降序排列；（2）按照公式计算成为自由个体的概率。

其中，ρα为个体α成为自由个体的概率，μ为行人α的排序值。

1.3  社会力驱动阶段

在SFSO算法中，在同一子群体内，行人α所受的社会力主要包括行人α的期望力和其它行人β对行人α的排斥力。行人α的社会力由公式定义。

式中：pα为行人α的当前位置，为行人α所选择的目标位置。

在SFSO算法中，行人的期望速度由公式确定。

行人的位置更新按照公式进行。

1.4  协作阶段

在SFSO算法中，个体间通过协作在历史记忆附近进行搜索。个体间的协作主要是通过分享各自的信息来进行的，分享信息包括当前位置信息和历史记忆信息两部分。个体α按照公式在历史记忆附近搜索新的位置。

2  SFSO在多变量PID控制器设计中的应用

PID控制算法由比例、积分和微分环节组成，PID控制器的传递函数见公式（15）。

式中：KP为比例系数；KI为积分系数；KD为微分系数。

一个典型的2输入2输出的蒸馏塔控制过程示意图如图1所示，该过程的传递函数矩阵如式（16）所示[3-4]。

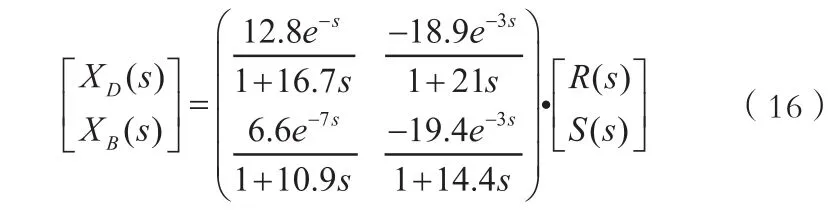
图 1 蒸馏塔控制示意图

针对该蒸馏塔控制过程的PID控制器如公式（17）所示。

利用SFSO算法优化设计多变量PID控制器时，其实质是寻找最优化PID参数，使控制系统在动态和静态性能上能够满足一定的性能指标要求，如：超调量、上升时间以及稳态误差、误差平方积分ISE、绝对误差积分IAE、时间与绝对误差的积分ITAE等。

利用SFSO算法对蒸馏塔多变量PID控制器参数（KP11KI11KP12KI12KD12KP21KI21KD21KP22KI22）进行优化时，参数的取值范围为[-1,1]，并采用公式（18）所示的IAE指标作为目标优化函数。

SFSO 算法的参数设置如下：N=30,Itermax=1000,ε=1,φ=0.001。SFSO算法最终获得的IAE的最优值为9.9319，获得的10个参数分别为KP11= 0.4285；KI11=0.1547；KP12=-0.3155；KI12=-0.0960；KD12=0.1173；KP21=-0.2083；KI21=0.0596；KD21=-0.2728；KP22=-0.1040；KI22=-0.0484。蒸馏塔的两个输出变量XD、XB的阶跃响应曲线如图 2所示。

从仿真结果可知，采用SFSO算法对PID控制器参数进行优化设计，系统阶跃响应具有超调量小、调节时间短等特点，能够快速跟随输入变化，保证系统响应指标满足蒸馏塔系统控制要求。

3 结束语

图2  蒸馏塔控制系统阶跃响应分析

蒸馏塔作为一类复杂的被控对象，其输入输出之间存在强耦合问题。针对蒸馏塔工艺控制需要，在研究分析的基础上，将智能SFSO优化算法应用于多变量PID控制器的参数设计。仿真结果表明，通过SFSO算法对多变量PID控制器参数进行优化设计，使系统获得了超调量小、调节时间短、抗干扰性能好等优点。