圆柱包容锁紧装置的失效分析与设计

徐 龙，裴永臣，袁德志

（1.吉林大学南岭校区机械与航空航天工程学院，吉林 长春 130025； 2.儒拉玛特自动化技术（长春）有限公司，吉林 长春 130103）

锁紧装置通常用于定位、承载和夹紧等，是许多机器中必不可少的部分。世界各地的研究人员已经研究了多种具有不同原理、方法和结构的锁紧装置。例如，Chen等人设计了一种在焊接过程中夹紧核燃料棒的机器，可在热辐射条件下使用[1]。Yang等人提出了使用巨型磁致伸缩材料TeDyFe的夹紧原理和相应方法[2]。Fassina等人设计了一个非整体的管夹连接器并进行了失效分析，指出应力值决定了它的失效[3]。Iyer等人基于三维有限元分析评估了干涉夹紧对单排铆钉疲劳寿命的影响[4]。Poursaeidi等人基于有限元分析软件ANSYS分析了燃气轮机中锁销的故障[5]。

圆柱包容锁紧装置是锁紧装置的重要组成部分，由于其结构简单，安装方便，成本低廉而被广泛使用。这类锁紧装置通过螺栓预紧力使立柱与圆柱孔之间产生摩擦力来平衡载荷。毫无疑问，不同的螺栓预紧力会产生不同的摩擦力，导致承载能力不同。操作员通常根据经验由预紧力估算承载能力，而结构参数或装配间隙的改变，会导致选择的预紧力不合适，发生例如塑性变形、断裂或承载能力不足等失效形式。

尽管圆柱包容锁紧装置已经发明了很长时间，但很少有人研究图1所示的3种圆柱包容锁紧装置的结构细节和失效模式。在本文中，提出了这3种锁紧装置的结构设计方法，得到了装配间隙和预紧力对承载力的影响，分析了失效模式。

1 建模和分析方法

本文选用的锁紧装置主体尺寸为800 mm × 800 mm ×200 mm，立柱为 100 mm，螺栓为M20。

图1   三种锁紧装置实物图

因其具有良好的对称性，故只需对1/4模型进行研究。首先分析对承载能力可能有影响的结构参数，如图2所示。

全封型：缝隙宽度a；侧壁厚度b；圆柱孔中心位置（X1，Y1）。缝隙型：长缝宽度d1；长缝距主体边缘的距离h1；短缝宽度d2，长度L；短缝距主体边缘的距离h2；圆柱孔中心位置（X2，Y2）。凹槽型：从边缘到圆柱孔中心的距离m；螺栓孔中心位置n；圆柱孔中心位置X3。

因为支反力减去主体的重力等于载荷，所以用更易获得的支反力代替承载能力，使用CATIA进行三维建模后导入ANSYS中进行仿真分析。

2 仿真分析及讨论

2.1 全封型

将预紧力选取为远小于螺栓承载极限的20000 N来探究各因素对锁紧装置承载能力的影响规律。设计了如表1所示的正交试验，试验结果按水平与因素求和进行分析，记录在表2中。

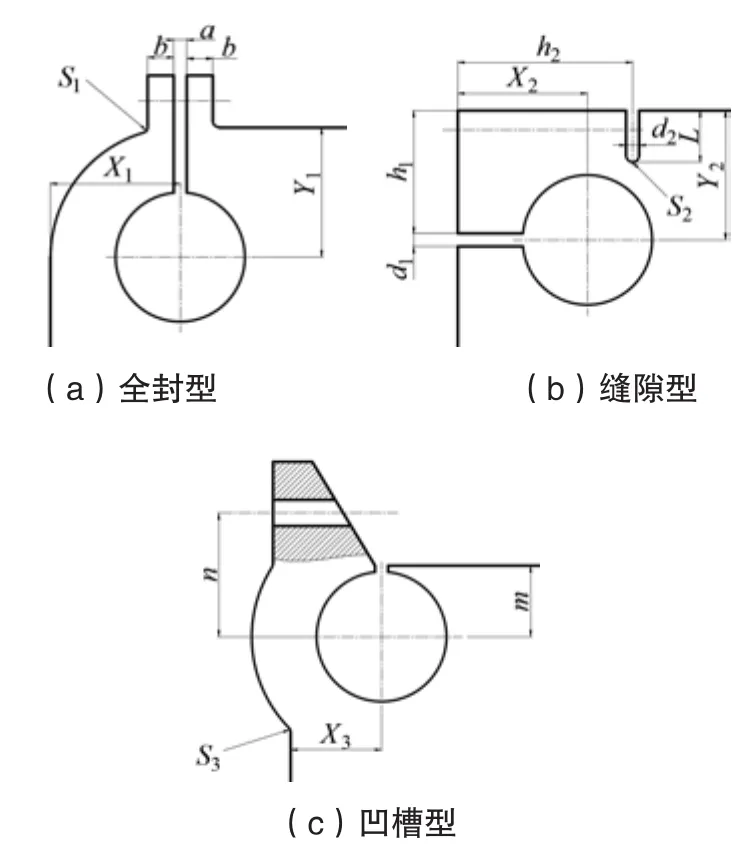
图2   三种锁紧装置结构及参数

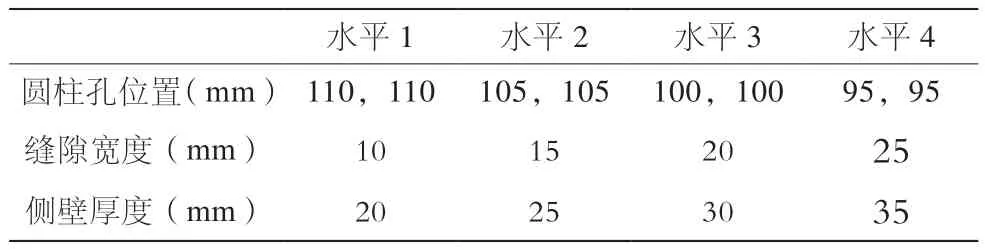
表1   全封型锁紧装置正交试验因素及水平取值

表2   全封型正交试验仿真结果分析

由正交试验结果分析可以得出：同预紧力下，圆柱孔位置越靠近边缘，锁紧装置的承载能力越强；缝隙宽度减小与侧壁厚度增大将增大锁紧装置的承载能力；3个因素的敏感性大小顺序为：缝隙宽度＞圆柱孔位置＞侧壁厚度。

根据力学原理及仿真应力云图，知应力集中位置为S1。由于圆柱孔位置的变化会改变该处壁厚，导致应力超过材料的屈服极限，应进一步分析。未发生屈服时，预紧力与应力的关系基本呈线性，可由试验数据通过线性插值得到其应力达到屈服极限355 MPa时的最大预紧力。将结果代回原模型中计算其最大支反力，结果见表3。在圆柱孔位置为（85，85）时全封型锁紧装置有最大承载能力，可承受载荷大小为85076 N。

表3   全封型的最大预紧力和支反力

综上所述，全封型锁紧装置的最优结构参数为：a=10mm,b=30 mm,(X1,Y1)=(85,85) mm。

以优化后的结构参数为基础进行装配间隙对承载能力影响规律的研究，得到如图3所示的响应曲面图。

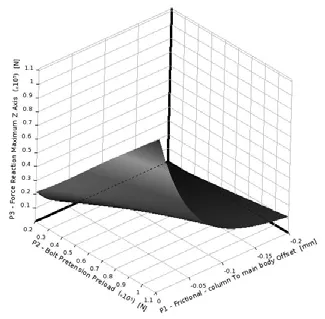
图3   预紧力、装配间隙与支反力响应曲面图（全封型）

从图3可看出，当装配间隙增大时，锁紧装置承载能力迅速衰减。为指导预紧力的选择，需要获得预紧力与承载能力之间的精确关系曲线，以H8/h7的间隙中间值为例给出关系曲线，如图4所示。

图4   预紧力与最大支反力关系图（全封型）

对于全封型锁紧装置，故障模式总结如下：应力集中位置S1处塑性变形；螺栓预紧力过小导致主体滑落；预紧力过大导致螺栓断裂。

通过仿真和分析，得出了以下几个设计建议。

（1）缝隙宽度应小于一定值，通常在5～15 mm之间；

（2）圆柱孔的位置具有最佳值，应通过仿真获得最佳值；

（3）侧壁的厚度对承载能力影响很小，但不能太薄以防止发生塑性变形；

（4）使用大圆角进行过渡，以减少S1位置的应力集中；

（5）装配间隙应尽可能小。

2.2 缝隙型

与全封型类似，缝隙型设计正交试验，各因素与水平取值如表4所示（d1与d2为10 mm、预紧力为20000 N），试验结果按水平与因素求和进行分析，记录在表5中。

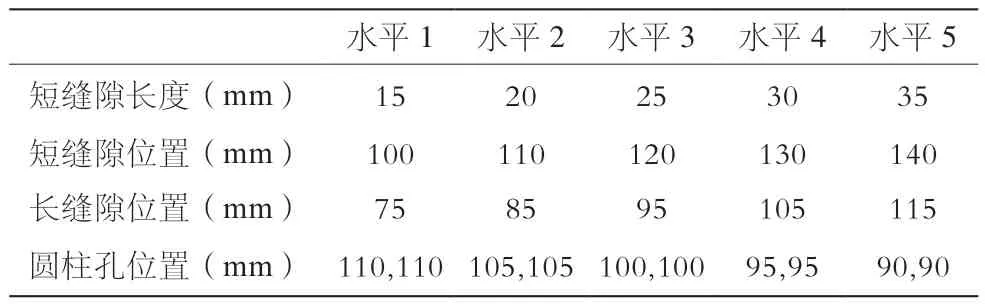
表4   缝隙型锁紧装置正交试验各因素水平取值表

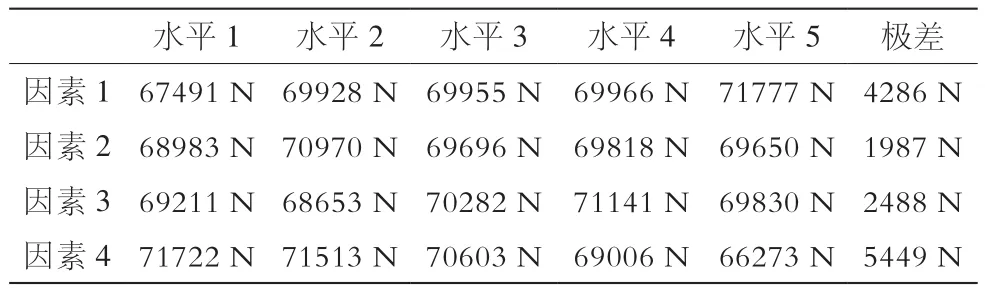
表5   缝隙型正交试验仿真结果分析

由正交试验结果分析得出：虽然圆柱孔位置远离边缘时锁紧装置的承载能力增大，但随着X2与Y2的增大，承载能力增长趋势减缓。当短缝隙长度L增大时，锁紧装置的承载能力也相应增大。各因素敏感性大小顺序为：圆柱孔位置＞短缝隙长度＞长缝隙位置＞短缝隙位置。

由于缝隙位置与圆柱孔位置存在交互作用，采用单变量法进一步分析长、短缝隙位置和宽度对锁紧装置承载能力的影响规律。选取正交试验中具有最大支反力的24号试验组的结构参数为基础进行探究。

发现当长缝隙对称面穿过圆柱孔轴线时锁紧装置有最大的承载能力。长、短缝隙宽度小于10 mm时，支反力在15100 N左右波动，相对变化量不到1‰，故认为在小于10 mm时对承载能力无影响。

该步仿真中发现，改变短缝隙位置时支反力最大值出现位置随圆柱孔位置改变而改变。由于短缝隙位置与圆柱孔位置存在交互作用，考虑与圆柱孔轴线的位置关系，最大值出现位置均为与圆柱孔轴线相距35 mm处，即h2=（X2+35）mm。

同样，对影响应力集中位置S2处壁厚的短缝隙长度L进一步探究。通过线性插值法得到在应力为屈服极限355 MPa时的预紧力大小以及最大支反力。结果记录于表6中，支反力随短缝隙长度的增加呈现出先增大后减小的趋势，在L=57.5 mm时出现了最大值。

表6   缝隙型的最大预紧力和支反力

综上所述，缝隙型锁紧装置的最优结构参数为：d1=10 mm，h1=100 mm，d2=10 mm，h2=（X2+35）mm，L=57.5 mm，（X2，Y2）=（105，105）mm。

以优化后的模型为基础进行装配间隙及预紧力对承载能力影响规律的研究。模拟过程与全封型相同，结果如图5所示，随着装配间隙尺寸的增加，承载能力将迅速下降。同样，给出了间隙大小为H8/h7中间值的预紧力与支反力关系曲线来指导预紧力的选择，如图6。

图5   装配间隙、螺栓预紧力与最大支反力响应曲面图（缝隙型）

缝隙型的失效形式除了应力集中位置不同外与全封型几乎完全相同，S2位置可能发生塑性变形。

通过仿真和分析，得出了以下几个设计建议。

（1）长缝和短缝的宽度对承载能力影响很小，适当控制即可；

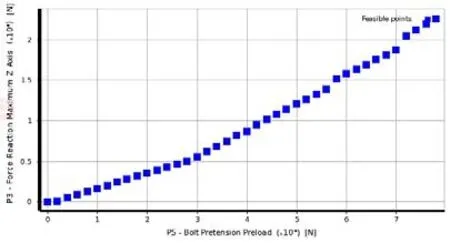
图6   缝隙型锁紧装置预紧力与支反力关系曲线

（2）圆柱孔的位置在承载能力增加趋势减缓的值附近选择；

（3）长缝的对称面应穿过圆柱孔的轴线；

（4）通过仿真获得合适的短缝位置和长度；

（5）使用大圆角过渡，减小S2位置的应力集中；

（6）增大螺母面积，减少主体与螺栓接触表面上的应力集中；

（7）装配间隙应尽可能小。

2.3 凹槽型

从前两种锁紧装置的分析经验来看，m、n与承载能力在一定范围内应具有良好的线性关系。为简化仿真分析过程，采用单变量法研究这些结构参数对锁紧装置承载能力的影响规律。

初始参数选取m为48 mm，螺栓孔位置n为98 mm，预紧力20000 N，圆柱孔位置为X3=40 mm。当m的值小于圆柱半径时，随着m的增大，支反力有明显增加，但m值超过圆柱半径后增长变得不明显，所以认为49.5 mm是参数m的较优解。螺栓孔位置远离圆柱孔轴线时同预紧力下锁紧装置的承载能力增大，但由于材料刚度的限制，螺栓孔位置过远时会产生局部变形，所以将螺栓孔位置选定为n=113 mm。

与前文类似，改变圆柱孔位置会导致应力集中位置S3处壁厚改变，对其进行进一步探究。得到最大预紧力与最大支反力，结果如表7所示。其中，因所选用的M20螺栓所能承受的最大预紧力为110000 N，故圆柱孔位置为40 mm与42 mm两组仿真的最大预紧力取为110000 N。结果表明，圆柱孔位置为40 mm时支反力有最大值。所以由以上仿真分析得到的凹槽型锁紧装置最优结构参数为：m=49.5 mm,n=113 mm,X3=40 mm。

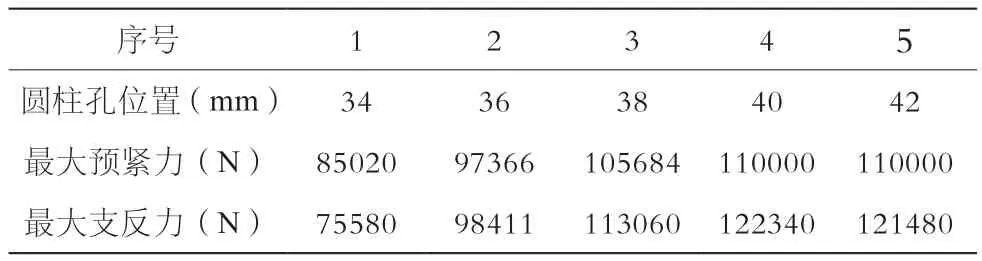
表7   凹槽型锁紧装置最大预紧力与最大支反力

以优化后的参数进行装配间隙及预紧力对承载能力影响规律的研究。模拟过程与全封型相同，结果如图7所示，随着装配间隙尺寸的增加，承载能力将迅速下降。针对凹槽型锁紧装置也给出了与之前相同间隙值情况下的预紧力与支反力关系曲线，如图7。

失效情况与前两种锁紧装置基本一样，应力集中位置为S3处。

通过前面的分析，可以得出有关凹槽型锁紧装置设计的一些建议。

（1）参数m应该比圆柱孔的半径稍大；

（2）最佳的圆柱孔位置X3需要通过仿真得到；

（3）随着螺栓孔位置n的增大，承载能力将增大，但是考虑到空间、材料刚度、成本等，不能选择过大的n，应考虑在40～60 mm之间选择；

（4）使用大圆角过渡，以减少S3位置的应力集中；

（5）装配间隙应尽可能小。

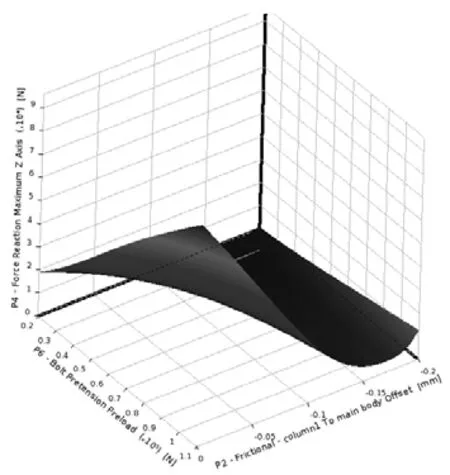
图7   预紧力、装配间隙与支反力响应曲面图（凹槽型）

图8   凹槽型锁紧装置预紧力与支反力关系

2.4 三种锁紧装置的对比分析

比较这三种锁紧装置，在相同的基本尺寸下，全封型的最大支反力为85076 N，缝隙型为72978 N，凹槽型为122340 N。因此，凹槽型锁紧装置具有最大的承载能力，全封型锁紧装置则比缝隙型锁紧装置稍好。因此，在需要大承载能力的场合，应考虑使用凹槽型锁紧装置。

从预紧力、装配间隙和支反力三者的响应曲面图可以看出，凹槽型锁紧装置的承载能力对装配间隙具有最大的敏感性。因此，在设计凹槽型锁紧装置时，应更加严格控制装配间隙。

3 结    论

本文提出了一种圆柱包容锁紧装置的结构优化方法。在分析失效模式的基础上，给出了一些设计建议。具体结果如下：

（1）提出了一种结构优化方法，采用正交试验法和有限元法对圆柱包容锁紧装置进行结构优化，获得了每个参数对承载能力的影响规律。

（2）通过仿真得到了预紧力与承载能力之间的定量关系，指导圆柱包容锁紧装置的设计及使用。

（3）立柱和圆柱孔之间的装配间隙对锁紧装置的承载能力有很大影响。装配间隙越小，承载能力越强。