自抗扰控制器的无摩擦气缸控制研究

刘 昱 ，王 安 ，2，刘昌龙 ，2，宋玉宝

（1.北京石油化工学院信息工程学院，北京 102617；2.北京化工大学信息科学与技术学院，北京 100029）

1 引言

气动系统因其实用性强，低成本，干净无污染，可靠性高，适应性强，发热率低等优点而发展迅速[1]。目前在汽车制造业、电子半导体制造业、航空航天、机器人、机械、化工等领域广泛应用。

气动伺服系统是一种特殊的气动系统，由气体压力产生驱动负载的输出力，其实质为压力控制[2]。因为气体的压缩性和管路系统产生的压力传递时延以及阀口的非线性流量特性，使气动伺服系统具有延迟和强的非线性，实现其高精度压力控制一直是重大难题。传统PID控制对系统高精度控制要求无法满足，因此，对气动伺服系统的压力控制进行新的控制策略研究，意义重大。

近年来，各国的气动研究者都为此做了大量的研究工作。文献[3]设计出一种多输入多输出的滑膜控制器，用低频正弦信号对气缸输出力和刚度的同步控制的跟踪效果较好；文献[4]提出线性状态反馈结合非线性补偿的复合控制方法研究气动力闭环控制，对正弦信号具有较好的控制效果；文献[5]设计出基于全阶热力学模型的气动伺服系统的自适应鲁棒控制器，保证了系统一定的瞬态性能和气缸输出力的高精度控制；文献[6]提出一种基于混沌粒子群的改进滑膜干扰观测器的控制方案，较好的解决气动伺服系统的延迟和非线性，具有较好的控制性能。基于Labwindows CVI软件开发平台，将自抗扰控制策略应用到气动伺服控制系统中，进行压力控制实验。实验结果表明自抗扰控制器控制精度高，响应快，对系统中的不确定性具有较强的抗干扰能力。

2 气动伺服系统模型

2.1 系统结构

主要基于比例流量阀及无摩擦气缸的压力控制系统研究。系统主要由比例流量阀（MPYE-5-1/8HF-010B）、无摩擦气缸、高精度压力传感器、研华PCL1716数据采集卡、工控机等组成，实验装置，如图1所示。

图1 压力控制实验装置Fig.1 The Experimental Device of Pressure Control

采用Labwindows CVI软件平台开发系统实时控制程序完成系统控制，将给定信号传送给比例流量阀控制压缩空气的流量，同时气缸腔内压力由高精度压力传感器实时测量，测量到压力数据通过数据采集卡传送给工控机。系统结构图，如图2所示。

图2 系统结构图Fig.2 System Structure Diagram

2.2 系统模型

考虑连接管路效应和气体流动的复杂性，为简化计算，现假设如下[7]：

（1）气体的流动为等熵过程；

（2）气体满足理想气体状态方程；

（3）管路对气压传递无影响；

（4）气体温度在流动过程保持不变。

2.2.1 比例流量阀模型

本实验研究采用FESTO公司的三位五通比例流量阀（MPYE-5-1/8HF-010B），为提高控制系统性能、降低模型复杂度，将阀的动力学模型视为一阶系统，并补偿阀的中位死区。

式中：kA、kfc—待定系数；Av—阀口有效截面积；U—电压实际输出信号；Uub、Ulb—为死区电压上下限，分别取 4.8V、5.2V。

气体通过阀口可看成流经过收缩喷管的无摩擦理想气体的等熵流动，故阀口流量方程为：

式中：Cf—流量系数；Av—阀口的有效截面积；pu、pd—流道前后压力；φ—流量函数；k—气体比热比；T—气体温度；bcr—临界压力比。对于空气，则k=1.4，R=287，C1=0.040418，C2=0.156174，bcr=0.528。

2.2.2 缸内压力模型

因无摩擦气缸的特殊结构导致其内泄流量不可忽略[8]。气体的泄露流量与气缸内压力在缸内压力达到稳态时，两者成正比关系，其模型方程为：

式中：kL，m0—待定系数。

由假设条件可知，缸内压力可用如下微分方程表示：

式中：Vc—缸腔总容积；mcin、mcout—气缸流入流出气体质量；pc—缸内压力。

若起始时活塞在气缸底部，则气缸总容积为：

式中：V0—气缸无效容积；Ac—气缸有效截面积；yc、Lc—活塞的位移和总行程。

2.2.3 控制系统模型

综合以上推导，该压力控制系统是一个二阶系统，近似模型为：

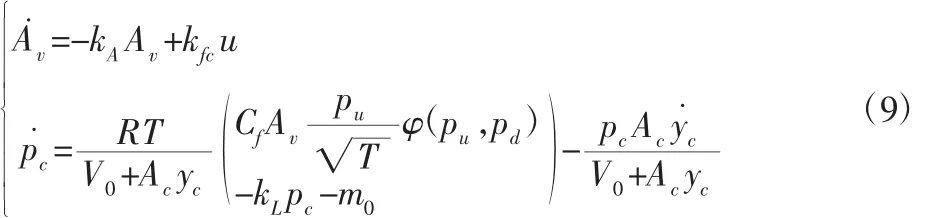
考虑控制目标为缸内压力，所以选取y=pc为系统输出变量，并对p˙c进行微分，选择新得的状态变量 X=［x1，x2］T=［pc，p˙c］T，将（9）变为规范化形式的状态方程：

充气时，Av=Avin，Avout=0；pu=ps，pd=pc；排气时，Av=Avout，Avin=0；pu=pc，pd=pa；其中 ps、pc、pa分别为气源压力、缸内压力、大气压力。

由上述过程可知，该系统是一个复杂的非线性时变系统，对模型参数无法精确获得，只获得了大致精确的数学模型，对控制系统的要求常规的PID控制算法难以满足。因此，需要引入一种新的控制算法来满足在模型、外界环境双重扰动下，仍能有很好的稳定性、动态性和跟踪精度。

3 自抗扰控制器设计

自抗扰控制器（Active Disturbances Rejection Controller，ADRC）由跟踪微分器（Tracking Differentiator，TD）、扩张状态观测器（Extended State Observer，ESO）、非线性状态误差反馈控制率（Nonlinear State Error Feedback，NLSEF）三部分组成[9]。ADRC 结构简单，并且不要求被控制对象的数学模型十分精确，可以实时估计补偿系统内外的总扰动，鲁棒性和实用性较强。

设有二阶被控对象：

式中：ω（t）—系统外扰；f（x1，x2，ω（t），t）—包含外扰与内扰的总扰动。以二阶系统为例，ADRC基本结构，如图3所示。

图3 ADRC基本结构图Fig.3 The Structure of ADRC

3.1 跟踪微分器（TD）

自抗扰控制器用TD来安排过度过程，获得光滑的输入信号，并对微分信号进行提取，在输入信号突变时有效减小超调，式（13）为跟踪微分器的离散化形式，由最速综合函数fhan构造。

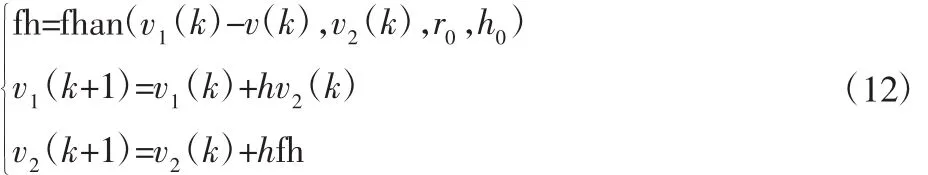
式中：fhan—最速控制综合函数；r0—速度因子；h0—滤波因子；h—采样步长。fhan（x1，x2，r，h）算法如下：

3.2 扩张状态观测器（ESO）

扩张状态观测器（ESO）将系统总扰动扩张成一个新的状态，然后利用系统的输入、输出重构（观测）出包含系统原有状态变量与扰动的所有状态[10]。对二阶对象，如式（11）所示。将系统总扰动f（x1，x2，ω（t），t）视为新的状态变量：x3（t）=f（x1，x2，ω（t），t）加入原系统中，使其扩张成一个新状态：

对此建立的状态观测器如下：

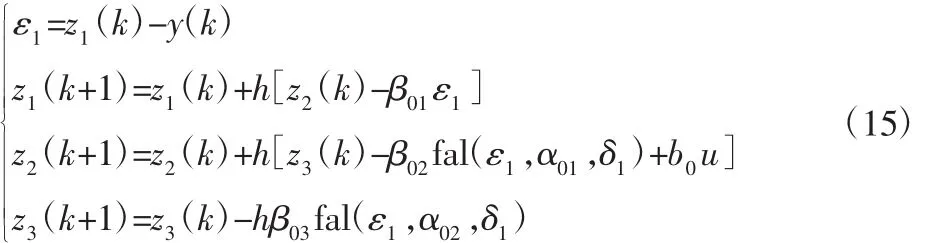
式中：b0—b 的估计值；z1、z2—x1、x2的实时估计；z3—系统“总扰动”的实时估计；β01、β02、β03—观测器参数；fal（x，α，δ）—非线性函数，α01、α02一般分别取 0.5，0.25，δ为线性区间长度估计。

3.3 非线性状态误差反馈控制率（NLSEF）

基于跟踪微分器和安排过度过程手段，可以跟踪产生过渡过程的误差信号，利用非线性函数fal（x，α，δ）构建非线性控制率，使稳态误差以幂函数形式递减，加快响应速度。

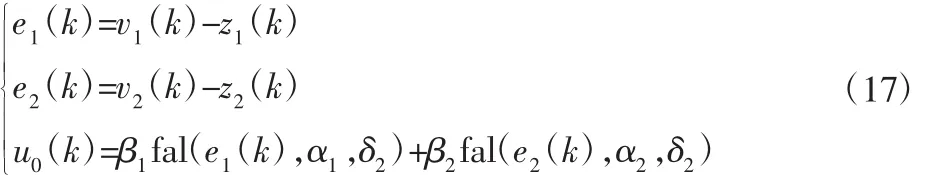
式中：β1、β2—增益系数，α1、α2的取值一般为 0<α1<1<α2。

实际上控制量u（k）由两部分组成，其中-z3（k）/b0是补偿扰动分量，u0（k）/b0是用非线性反馈来控制积分器串联型的分量。

扰动补偿形成控制量：

4 实验结果分析

本实验装置的关键参数，如表1所示。实验前，将气缸活塞杆固定，使气缸容积保持不变，对该系统分别使用PID控制算法和ADRC控制算法的压力控制实验。实验采样频率为100Hz，实验数据均未滤波处理。

表1 系统关键参数表Tab.1 System Key Parameter Table

在初始状态下，做0.1MPa的阶跃响应实验，其阶跃响应曲线，如图4所示。稳态误差的局部放大曲线，如图5所示。待系统稳定后，在第40s时对系统施加一个瞬时干扰，响应曲线，如图6所示。

图4 阶跃响应对比曲线Fig.4 Step Response Curve

图5 稳态误差曲线Fig.5 Steady-State Error Curve

图6 瞬时扰动响应曲线Fig.6 Instantaneous Disturbance Response Curve

在初始状态下，PID控制和ADRC控制跟踪幅值为0.1MPa，频率分别为0.02Hz和0.04Hz的正弦信号，正弦跟踪曲线，如图7所示。通过实验结果分析由图4得，在初始状态下，该系统在PID控制下的阶跃响应调节时间约为19.6s，稳态误差约为0.000625MPa，在ADRC控制下的阶跃响应时间约为14.4s，稳态误差约为0.000316MPa。与PID控制相比较可得，采用ADRC控制该系统的阶跃响应调节时间缩短了约26.53%，稳态误差减小了约49.44%。通过瞬时扰动实验结果图6分析得，ADRC抗干扰恢复时间约为6.9s，PID恢复时间约为11.4s；可见ADRC抗干扰和恢复能力相较于PID要更好。

图7 正弦跟踪响应对比曲线Fig.7 Sine Tracking Response Curve

对正弦信号跟踪分析由图7得，对幅值为0.1MPa，频率为0.02Hz的正弦信号跟踪：PID控制下系统平均跟踪误差约为0.012695MPa，ADRC控制下系统平均跟踪误差约为0.005396MPa，大约为PID的42.5%；对幅值为0.1MPa，频率为0.04Hz的正弦信号跟踪：PID控制下平均跟踪误差约为0.016173MPa，ADRC控制下平均跟踪误差约为0.009325MPa，大约为PID的57.66%。

综上实验结果分析得，相比较于传统PID，基于ADRC控制的系统压力控制精度更高，控制效果更加优异。

5 结论

将ADRC控制算法用于无摩擦气缸伺服系统的压力控制，有效的克服了气缸伺服系统的强非线性问题，满足了系统高精度压力控制的要求。利用TD来安排过度过程获得光滑的输入信号和微分信号提取，采用ESO对系统状态实时观测并对系统的总扰动进行估计补偿，设计带有总扰动补偿的非线性反馈控制率（NLSEF）来确保闭环系统的良好性能。最后通过实验比较，ADRC与传统PID相比较，其控制效果更加优异，控制性能更好，因而此方法在气动伺服系统的控制器设计中具有很好的实际意义。