社会消费品零售总额预测

刘娜

摘要：现运用ARIMA模型、BP神经网络模型以及构建的组合预测模型，对1985-2018年我国社会消费品零售总额进行分析。研究发现预测误差平方和倒数模型预测为最优模型，预测精度高达98.65%，预测结果显示2019-2021年我国社会消费品零售总额分别为405106.5653、426571.6308、446393.2806亿元，总体呈现增长趋势。

关键词：社会消费品零售总额;ARIMA模型;BP神经网络模型;组合预测

中图分类号：F740    文献标识码：A

文章编号：1005-913X（2020）05-0036-03

社会消费品零售总额是指企业或者单位，通过交易售给个人、社会集团，非生产、非经营用的实物商品金额，以及提供餐饮服务所取得的收入金额。2018年我国社会消费品零售总额380 986.9亿元，相比2017年增长4.2% ，截止2019年12月，全国社会消费品零售总额同比增长8.0% 。社会消费品零售总额大小直观地反映居民消费水平以及零售业经济发展状况，其精准分析与预测对于有关部门相关政策的制定以及重大事件决策具有一定的参考价值。

一、模型介绍

（一）ARIMA模型理论

ARIMA模型又称单整自回归移动平均模型，属时间序列短期预测分析方法之一。时间序列分析主要是根据已有的历史数据对未来年份进行预测。本文采用图示法和单位根检验相结合检验;数据平稳化处理，对于非平稳并且含指数趋势的时间序列，需先取对再进行差分处理;模型建立，确定参数跑（p，d，q）建立时间序列模型;模型检验，做残差检验诊断残差序列是否为白噪声序列;模型预测，使用R中的forecast包对拟合的ARIMA（p，d，q）模型进行预测。

（二）BP神经网络模型理论

BP神经网络是一种多层前馈神经网络，它是模仿人类大脑神经元的一种模型，它的运行路线是信号向前传递，误差则是反向传递。在向前传递时，将数据录入到输入层，经过隐含层的处理，经输出层输出。如果输出结果不是期望值，则进入反向传递过程，通过不断地调整权值和阈值从而进一步优化输出值，使其接近或等于期望值。BP神经网络分为训练和测试两个过程，训练过程是让模型具有记忆和预测的能力。神经网络流程如图1所示，其中为X输入值，Y为预测值，W为权值。

（三）ARIMA与BP神经网络组合模型

单个预测模型在预测的过程中不可避免的会出现误差，组合模型的建立能够有效减少误差。其基本思想就是充分利用单个预测方法所包含的独立的信息，对单个模型的预测结果进行加权处理。

等权法：通过给需要组合的各个模型结果，给予相同的权重。等权法可以有效避免精度大权重小、精度小权重大，并且计算简单操作方便。

预测误差平方和倒数法：预测模型误差平方和越小，表明该项预测模型的精度越高，它在组合模型中的重要性越高，公式如下，其中Dj为第j个模型的误差平方和：

误差方差均方倒数法：它是对预测误差平方和法的改进两者原理基本一样其公式如下，其中Ej为第j个模型的误差方差：

预测精度，其中Ei是相对误差：

二、实证分析

本研究数据来自国家统计局官网公布的1985-2018年社会消费品零售总额数据。文章保留2016-2018年的数据作为检验模型数据，1985-2015各年数据作为样本数据，所用软件为Matlab 2016a和R 软件3.6.2。

（一）建立ARIMA模型预测

1.模型建立

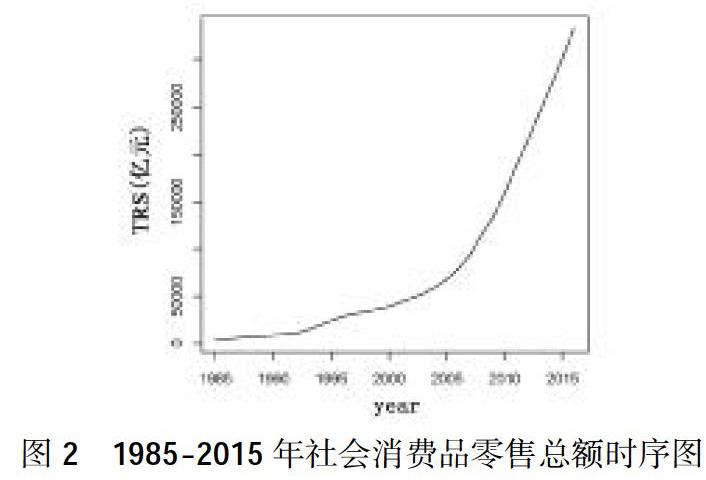
平穩的时间序列是建立时间序列模型的基础，如果时间序列图像有明显的趋势性或者规律性，此时序列平稳，反之则非平稳。如图2所示为1985至2015年社会消费品零售总额时间序列图，从图中可知在1985-2010年有上升趋势但是总体较为平缓。而2010年之后则以十分明显的呈指数趋势上升，序列不平稳。取对后的数据，消除了指数上升趋势，但其序列仍然不平稳，对于非平稳的数据进一步做差分处理，利用R软件中的ndiffs（）函数可知需进行二阶差分处理，结果如图3所示，序列在某一常数附近上下波动，并无明显上升或者下降趋势，此时序列平稳可以建立模型。

图示判断简单直观，但往往带有一定的主观性，基于此本文采用ADF检验法，对时间序列平稳性进行检验。用R软件做单位根检验，结果显示p-value = 0.01<0.05，此时拒绝原假设即序列平稳，可以构建ARIMA模型。为确定拟合情况最好的ARIMA模型阶数，通过自相关函数和偏自相关函数图确定的模型阶数 、R软件中的auto.arima（ ）包自动确定ARIMA模型的阶数一致，即文章最终确定模型ARIMA（0，2，0）。

2.模型检验、预测

为了检验ARIMA模型显著性，进行Ljung-Box法做残差检验，经检验p-value = 0.7718> 0.05，不能拒绝原假设认为模型显著有效。对保留的2016-2018年数据进行模型验证，模型预测结果显示2016-2018年我国社会消费品零售总额分别为333041.30、365877.90、399543.50亿元，同实际值相比，预测误差的方差2.82%，预测精度97.18%，说明模型预测效果较为可靠，ARIMA（0，2，0）可以拟合模型。

（二）建立BP神经网络模型进行预测

1.数据预处理

现将1985-2015年社会消费品零售总额指标作为输入，将2019-2021年社会消费品零售总额指标作为输出。对于原始数据进行预处理，能够将模型拟合的精度提高，为了让网络快速收敛，本文所选的是S型函数，归一化公式如下：

2.模型訓练

输入输出层的设计，本文采用含有一个隐含层的单输出的BP网络建立预测模型。目前，对于隐含层中神经元数目的确定目前并没有明确的公式，本文在选取隐含层神经元个数时，采用学者通常采用的经验公式：l=+a，其中n为输入层中神经元的个数，m为输出层中神经元的个数，a为1-10之间的常数。根据公式（1.14）可以计算出神经元个数在2-11个之间，经过大量反复试验，本文最终选取隐含层神经元个数为4。根据社会消费品零售总额的数据特征，本文选择输入层为2，输出层为1，即构建一个输入层、隐含层、输出层节点数为 2-4-1 的三层网络结构。

本文选择S型函数作为隐含层神经元的激励函数，将用来训练样本的数据先进行归一化处理，归一化后输入网络，并且设定网络参数，网络迭代次数epochs=5000次，期望误差goal=0.00065，学习速率lr=0.0354，设定完参数后开始训练网络。

3.模型预测

通过网络训练，得到2016-2018预测值分别为329667.20、350160.87、367478.81亿元。经计算，实际值与预测值相对误差为2.92%，预测精度为96.71%，预测误差的方差3.29%，结果在可接受范围内，但是比ARIMA模型预测精度低了0.47%。

（三）ARIMA模型与BP神经网络模型预测

为了充分利用两种模型各自的优势，对于ARIMA模型、BP网络模型分别提取不同数据信息，数据的线性部分由ARIMA 模型提取，非线性部分由神经网络提取。其基本思想就是对ARIMA模型、BP神经网络模型通过科学赋权重的方法，给定两个模型不同的权重，通过加权计算得出最终的预测结果。常见的确定权重的方法众多，但是符合本文数据特征的方法有：等权法、预测误差平方和倒数法、误差方差均方倒数法。

误差方差均方倒数模型：根据公式（1.10），利用EXCEL计算得知，给定ARIMA、BP网络分别0.409、0.591的权重，依据误差方差均方倒数模型，对预测2016-2018年数据进行拟合，计算预测相对误差计算结果如表1所示，从结果看出等权法的预测误差的方差为1.54%，预测精度为98.46%，比ARIMA模型的预测精度高了1.28%，比BP网络模型预测精度提高了1.75%，拟合情况较好。

等权组合预测模型：给定ARIMA和BP神经网络分别相同的权重得到组合模型，再根据组合模型对2016-2018年数据进行预测，计算预测相对误差如表2所示，从结果看出等权法的预测误差的方差为1.36%，通过公式计算预测精度为98.64%，相比于误差方差均方倒数模型预测精度提高了0.18%，拟合情况更优。

预测误差平方和倒数模型：根据公式（1.9）借助EXCEL计算得知， ARIMA和BP神经网络权重分别为0.578、0.422，利用得到的组合模型预测结果如表3所示，从结果看出预测误差平方和倒数法的预测误差的方差为1.35%比其他模型都小，预测精度提高到98.65%。

对模型进行组合时权重计算方式的不同会导致其组合模型精度也不同，所以在对单一模型进行组合时要结合数据本身的特征且从不同方面考虑其得到最优模型。根据对比几种预测模型的预测精度以及预测误差方差的大小，得到本文最优的组合模型为预测误差平方和倒数模型，几种模型具体对比结果如下表。

[表4 几种模型分析结果][模型 预测精度 预测误差的方差 ARIMA模型 97.18% 2.82% BP神经网络模型 96.71% 3.29% 误差方差均方倒数模型 98.46% 1.54% 等权组合预测模型 98.64% 1.36% 预测误差平方和倒数模型 98.65% 1.35% ]

3.基于组合模型预测

文章借助最优拟合模型预测误差平方和倒数模型，对2019-2021年我国社会消费品零售总额进行预测，2019-2021年社会消费品零售总额分别为405106.5653、426571.6308、446393.2806亿元，我国社会消费品零售总额在不断增长。

三、结论

本文运用预测误差平方和倒数模型进行预测，预测误差较小、精度较高、拟合情况较好，预测结果显示，2019-2021年我国社会消费品零售总额有增长趋势，鉴于文章是根据历史数据做预测，对于外生不可抗因素的干扰无法应对。

参考文献：

[1] 李庭辉，许涤龙.基于匹配性的社会消费品零售总额数据质量评估研究[J].统计与决策，2012（8）：24-27.

[2] 吕艳丽，陈兵建.基于ARMA模型的城乡居民收入差距分析与预测——以甘肃为例[J].区域经济，2017（2）：204-206.

[3] 肖学培.季节性ARIMA模型对社会消费品零售总额的建模和预报[J].经济研究，2019（4）：63-65.

[4] 王冬冬.基于ARIMA和BP神经网络模型的重庆市GDP实证分析[D].桂林：广西师范大学，2019.

[5] 刘海萍，王海涛，王洪利，等.基于BP神经网络的CPI预测模型[J].山东交通学院学报，2009，17（3）：83-86.

[6] 崔 博.神经网络在GDP预测中的应用[J].信息技术，2011（2）：103-105.

[7] 桂 梅，刘莲花.基于ARIMA模型对海南省社会消费品零售总额的预测[J].2017，2（3）.

[责任编辑：庞 林]