基于压缩感知的一种改进射电图像重建算法

潘润宁

摘  要： 针对射电天文图像重建中由于越来越大的数据集产生的保证与提高图像重建质量的问题，提出一种基于压缩感知技术的射电干涉图像凸优化重构算法。该算法对原始对偶算法引入迭代收缩算子和阈值模型，迭代收缩算子在每一步迭代过程中利用前两点进行组合更新，迭代过程更为精确，通过阈值模型克服不连续性产生的伪吉布斯效应，使得重建射电图像光滑并保留了有用高频信息。实验结果表明，改进算法在信噪比与重建精度方面优于PD算法，得到了更好的效果。

关键词： 射电图像重建; 压缩感知; 原始对偶算法; 射电天文观测; 凸优化算法; 阈值去噪

中图分类号： TN911.73?34                       文献标识码： A                         文章编号： 1004?373X（2020）09?0046?05

An improved radio image reconstruction algorithm based on compressed sensing

PAN Running

（MOE Key Laboratory of Cognitive Radio and Information Processing， Guilin University of Electronic Technology， Guilin 541004， China）

Abstract： For the poor image quality due to growth of data sets increasingly in the radio astronomical image reconstruction， a radio interference image convex optimization reconstruction algorithm based on the compressed sensing technology is proposed to ensure and improve the image quality. For the proposed algorithm， an iterative shrinkage operator and a threshold model are introduced into the primal dual algorithm. On the basis of the first two points， the iterative shrinkage operator implements combination update in each step of iteration to obtain more accurate iteration process， and the pseudo?Gibbs effect caused by discontinuity is overcome by the threshold model， which makes the reconstructed radio image smooth and useful high?frequency information retained. The experimental results show that the improved algorithm is superior to the PD algorithm in terms of signal?to?noise ratio （SNR） and reconstruction accuracy， and achieves a better effect.

Keywords： radio image reconstruction; compressed sensing; primal dual algorithm; radio astronomical observation;  convex optimization algorithm; threshold denoising

0  引  言

宇宙一直是人类进行探索的重要目标，从探知某一颗星体地表的结构，以至于到外太空之中是否存在着其他的生命文明，是否拥有可以被人类利用的物资资源等，这些信息可以由天文图像获得。到目前为止，射电天文图像重建中比较成熟的技术路线采用的算法大部分是以洁化算法[1]和最大熵算法[2]作为核心思想而进行改进的算法，而这两种算法并没有在理论和实际上解决欠采样问题。文献[3]发表的压缩感知理论为解决该问题提供了可能性。压缩感知引入了一种新的优于传统奈奎斯特采样的信号重建框架，相比于传统成像方法，在计算速度、灵活性和数据保真度方面有较大优势[4]。文献[5]利用压缩感知框架研究宇宙射线成像算法，比传统算法获得了更好的性能。文献[6]提出基于压缩感知的SparseRI，多功能圖像重构技术。文献[7]提出一种基于压缩感知理论新的解卷积的方法，用于恢复点源或展源图像，获得比传统算法更好的性能。文献[8]提出一种用于射电图像重建的原始对偶算法（PD），通过原始问题和对偶问题间的迭代得到重建结果。本文在基于PD算法的基础上，提出一种改进的算法，对射电图像得到了更好的重建质量，提高了重建图像的精度。

1  射电干涉成像

射电干涉测量天体是由一系列的阵列望远镜来虚拟综合等效口径及高角分辨率进行实现的。阵列望远镜测量天空亮度的强度数据，即射电干涉的能见度数据是在空间频率域中。Van?Cittert?Zernike理论指出了可见度[V（u，v）]和源亮度函数[I（l，m）]之间的关系：

[V（u，v）=I（l，m）e-i2π（ul+vm）dldm] （1）

式中：[（u，v）]是空间频率域的坐标;[（l，m）]是图像域的坐标。但是在现实测量中，采样是不完全的。对源亮度函数利用采样函数[S（u，v）]进行[u?v]覆盖后，得到可见度函数[V]与测量亮度[I（l，m）]的关系：

[I（l，m）=S（u，v）V（u，v）e-i2π（ul+vm）dudv]  （2）

通过离散重写式（2），得到一个线性测量模型：

[y=Φx+n]  （3）

式中：[x]为天空亮度;[y]为测量值;测量算子[Φ∈C?M×N]，映射图像域与[u?v]能见度空间;[n]为噪声。

由于望远镜的物理位置以及采样方案的局限性，使得式（3）成为一个不适定逆问题。测量算子[Φ=GMFZ]，其中，[G]为卷积差值算子矩阵，引入分块矩阵[M]，[F]为过采样傅里叶算子，[Z]为预补偿差值缩放算子。压缩感知理论指出，绝大多数信号通过一个字典[Ψ]能够有稀疏表示，[Ψ?x]只包含有少量的非零元素。从而可以通过解决以下不适定逆问题恢复信号[x]：

[minxΨ?x1s.t.    y-Φx2≤ε]   （4）

式中：[Ψ?]为[Ψ]的伴随算子;[ε]为噪声[l2]范数的上界。在此框架下，采用SDMM算法能够对数据进行分布式处理，但每次迭代都需要求解线性方程组，这样使得恢复大图像时需要的计算量很大。相比之下，PD算法的梯度算子、接近算子以及线性算子都可以单独使用，这与其他方案相比，在计算上具有很大的优势。

2  原始?对偶算法基本思想

现在引入求解约束优化问题的方法，即原始?对偶算法，其思想是通过对偶问题来对原始问题进行求解，就必须使得原始问题与对偶问题的最优值相等。考虑如下约束最优化问题：

[min f0（x）s.t.    hi（x）=0，    i=1，2，…，m          gj（x）≤0，    j=1，2，…，n] （5）

式（5）称为约束最优化问题的原始问题，将其构建为拉格朗日函数如下：

[L（x，λ，v）=f0+i=1mλifi（x）+i=1nvihi（x）]   （6）

那么，在满足约束条件下有：

[minxP（x）=minxmaxλ，vL（x，λ，v）=minxf（x）] （7）

即原始的优化问题与[minxP（x）]等价，则原始问题的最优值为：

[p*=minxP（x）]   （8）

然后考虑原始问题的对偶问题如下：

[maxλ，vD（λ，v）=maxλ，vminxL（x，λ，v）]     （9）

定义对偶问题的最优解为：

[d*=maxλ，vD（λ，v）] （10）

当原始问题和对偶问题都有最优解时，得到：

[d*=maxλ，vminxL（x，λ，v）≤minxmaxλ，vL（x，λ，v）=p*]  （11）

当原始问题的最优值与对偶问题的最优值相等，即[p*=d*]时，就可以用求解对偶问题来对原始问题进行求解。

3  改进的射电图像重建算法

3.1  射电干涉成像的原始?对偶问题

文献[8]提出了一种新的凸优化算法，将凸优化算法引入到射电干涉成像之中，在压缩感知的框架下，可以将成像任务写成如下形式：

[minxf（x）+l（Ψ?x）+h（Φx）]  （12）

式中[f=ιC（z）]，[ιC（z）]是凸集[C?RN]的指示函数：

[ιC（z）=0，    z∈C+∞，    z?C]  （13）

[h（z）=ιB（z），B=z∈C?M：z-y2≤ε]表示数据保真度项，该项对残差约束为低于由噪声水平[ε]定义的[l2]范数边界，[l=?1]表示给定的完备字典[Ψ]的稀疏先验性。

将原始对偶算法的思想应用到式（12）定义的最小化任务中，得到原始问题和对偶问题如下：

[minxf（x）+γl（Ψ?x）+h（Φx）]   （14）

[minu，vf*（（-Ψu-Φ?v）+1γl*（u）+h*（v））] （15）

式中：[γ]是一个附加的调整参数;[u]，[v]是对偶变量，算法收敛到一个库恩塔克点[（x，u，v）]，[x]即为原始问题的解，[（u，v）]则为对偶问题的解。[γ]的取值不會影响优化问题。解决成像问题即在原始问题式（14）与对偶问题式（15）之间迭代交替求出最优解。

3.2  改进的原始?对偶算法

3.2.1  迭代收缩算子

具有向前?向后迭代结构[9]的原始对偶算法框架，对于解决式（14）和式（15）具有较好的并行与可扩展性，在存储器需求和每次迭代的计算负载方面有较大的灵活性，但成像精确度不足，并且在低迭代次数时算法的重建结果信噪比较差。为了提高大视场下高分辨率天文图像的成像质量，针对存在的缺陷问题，在PD算法[8]基础上提出改进算法1。在提升图像重建结果信噪比的同时，考虑低迭代次数时信噪比过差的问题。

算法1

1.  输入[x（0），x（0），v（0），u（0），v（0），α，τ，κ，?，σ]

2.  重复[t=1，2，…]

3.  [p（t）=MFZx（t-1）]

4.  [v（t）=（I-ΡB）（v（t-1）+Gp（t））]

5.  [v（t）=v（t-1）+α（v（t）-vt-1）]

6.  [v（t）=G?v（t）]

7.  [u（t）=（I-ΓκΨs）（u（t-1）+Ψ?x（t-1））]

8.  [u（t）=u（t-1）+α（u-u（t-1））]

9.  [u（t）=Ψu（t）]

10. [x（t）=PC（x（t-1）-τ（Z?F??M?v（t）+σu（t）））]

11. [x（t）=x（t）+tk-1tk（x（t）-x（t-1））]

12. [x（t）=x（t-1）+α（x（t）-x（t-1））]

13. [x=2x（t）-x（t-1）]

14. 直至收敛

根据FISTA[10]技术，引入迭代收缩算子：

[tk+1=λ1λk+1+λ21λ2k+1+4t2k2，             t1=λ1， （λk）k≥1?ε，1， ε∈0，1] （16）

式中[λ]为可调节参数[11]，可以使得迭代收缩算子拥有更大的灵活性。

步骤10，步骤11中运用迭代收缩算子，不单是通过前一次迭代求得函数最小点[xk-1]，而且在迭代过程中利用前两点[xk，xk-1]进行特定的线性组合更新得出[x]，由此每次得到的迭代结果更为准确。

3.2.2  改进的阈值模型

引入文献[12]中的阈值模型对原算法进行改进。由于软阈值模型构造的稀疏先验函数存在原始信号估计不准确的问题，[Ψ?x]的系数由固定的阈值进行收缩，具有恒定误差[13]，会丢失一些有用的高频信息，可能使得重构图像存在边缘模糊等现象，损失图像的细节，也可能导致重建系数和原始系数间产生偏差。鉴于软阈值自身所具有的缺陷，使用改进的阈值模型为：

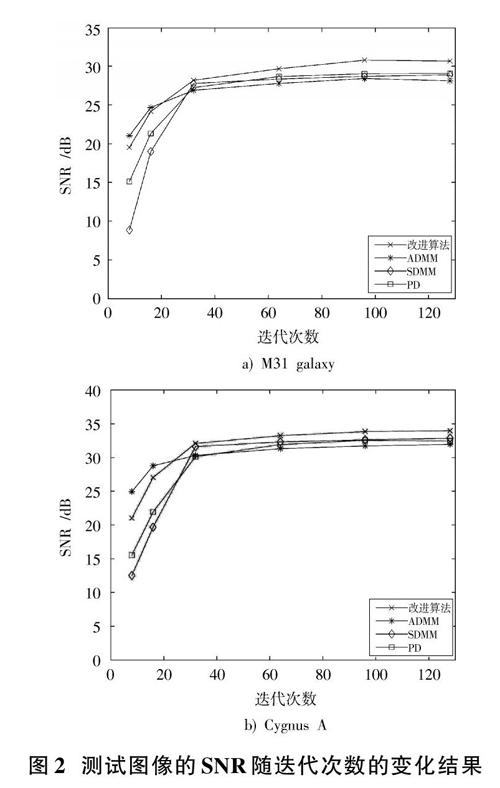
[ΓT（z）=sgn（z）z-Texpz-Ta，    z≥T0，    z

式中：[a]是一个调节因子，使得该阈值模型具有灵活可调性，针对含噪信号进行改变，可以获得去噪效果更优的阈值函数曲线;[sgn（）]是符号函数。新的阈值模型能够克服不连续性产生的伪吉布斯效应，使得重构图像更加光滑，有更好的去噪效果。

改进的原始?对偶算法如算法1所示。所有的对偶变量在步骤4～步骤9中并行更新。步骤4通过应用共轭函数[h*]的接近算子，将残差约束到[l2-ball]上以实现数据保真度，这就接受了一个封闭形式的解投影到[l2-ball]上：

[PB（z）?εz-yz-y2+y，    z-y2>εz，    z-y2≤ε]    （18）

步骤10中通过对偶变量[v（t），u（t）]对原始变量进行类子梯度更新，投影到凸集[C]上：

[PC（z）??（z），    ?（z）>00，    ?（z）≤0]   （19）

然后送到步骤11中用迭代收缩算子更新，最后在步骤12中得到[x（t）]。其中，[κ]为无标度参数，[?，σ，τ]为更新步长，[?=1Φ2S]，[σ=1Ψ2S]，[τ=0.49]，[α]为松弛因子。

4  仿真实验

为了测试改进算法对射电天文图像的重构性能，下面通过实验仿真进行评估，并与其他三种算法（交替方向乘子法（ADMM）、同时同向乘子法（SDMM）以及原始对偶算法（PD））进行比较。实验中，使用高斯采样随机生成[u?v]覆盖，为了模拟RI中通常存在的不完全采样，使用逆高斯分布在高频数据中引入空穴。稀疏先验使用SARA小波集合[14]，基集合分为[nd=9]个单独基，第一个是狄拉克基，其他8个基为Daubechies小波的前8个Db1～Db8。小波等级设置[n=4]。插值内核矩阵[G]使用[8×8]Kaiser?Bessel进行插值，平均近似均匀分布的频率值，以估计与每个可见度相关的频率处的值。过采样因子设置为4。由于宇宙噪声服从高斯分布，实验中通过引入高斯白噪声对原始数据进行干扰，输入信噪比为[PISNR=20logy02n2]，[y0]为洁净的测量矢量，计算可见度[M]下进行图像重构的平均信噪比。算法的重构性能由信噪比，即真实天空的标准偏差[σx]与估计模型的标准偏差[σx-x]的比值来定义：

[PSNR=20lgσxσx-x]   （20）

对于实验中的算法，其终止标准为全局残差范数[j=1ndyi-Φjx（t）22]低于阈值[ε2=（2M+34M）σ2] ，或迭代满足[l2]约束条件，并且[δ≤δ]解范数变化很小时终止，其中，[δ=x（t）-x（t-1）2x（t）2]。

实验中测试用图如图1所示。其中，以[lg]为标度。

首先研究在不同可见度[M]下本文算法以及其他三种算法的重构性能。以M31 galaxy图像为例，如表1所示，输入数据分为16块，ISNR为20 dB，设置最大迭代次数为100次，得到可见度[M]分别在10[N]，5[N]，2[N]，1[N]时重建结果的信噪比。结果表示在各个可见度设置下，本文算法均优于PD，ADMM，SDMM三种算法的重构质量。可见度为1[N]时，重构得到的SNR优于其他算法1 dB左右;可见度为10[N]时，重构后的SNR比其余三种算法约有2 dB左右的增益，随着可见度数据的增加，优势更加明显。

接下来研究本文算法随着重构迭代次数变化得到的SNR结果的变化情况。以M31 galaxy和Cygnus A图像为例，输入数据分为16块，ISNR为20 dB，可见度[M=][10N]。如图2所示，本文算法在迭代稳定后，信噪比均高于PD，ADMM，SDMM三种算法，能够得到更好的射电图像质量。在较低迭代次数时，较之改进前的PD算法，信噪比有更显著的提升，并且约为SMDD算法的2倍。

重建结果如图3所示。以W28 supernova remnant为例，图3a）为本文算法重建结果（29.36 dB）;图3b）为PD算法重建结果（27.12 dB）。参数设置在可见度[M=2N]，输入数据分为16块，ISNR为20 dB。两个重建效果图显示本文算法较PD算法获得的质量更高，图像更清晰，边缘表现更为细腻，能保留更多的高频信息，在信噪比上提高了2 dB，有较少伪影。而PD算法则丢失了较多图像细节，光源外沿模糊。本文算法在使边缘轮廓较PD算法更为清晰的基础上，能保留更多的射电图像细节，在结构内部区域中也拥有更好的表现。

5  结  语

为了提高射电图像重建质量，本文提出了一种改进的基于压缩感知的射电图像重建算法。该算法在原始对偶算法的基础上，利用迭代收缩算子和阈值模型精确重构原始信号并提高算法魯棒性。实验仿真结果表明，本文算法有效地提高了重构图像的精度和质量。

参考文献

[1] H?GBOM J A. Aperture synthesis with a non?regular distribution of interferometer baselines [J]. Astronomy & astrophysics supplement， 2011， 15（15）： 417.

[2] FOCSA A， TOMA S A， DATCU M. Maximum entropy image reconstruction applied to C?band ground based synthetic aperture radar [C]// 2017 IEEE International Geoscience and Remote Sensing Symposium （IGARSS）. Fort Worth， TX， US： IEEE， 2017： 3437?3440.

[3] CANDES E J， ROMBERG J， TAO T. Robust uncertainty principles： exact signal reconstruction from highly incomplete frequency information [J]. IEEE transactions on information theory， 2006， 52（2）： 489?509.

[4] WIAUX Y， JACQUES L， PUY G， et al. Compressed sensing imaging techniques for radio interferometry [J]. Monthly notices of the Royal Astronomical Society， 2017， 395（3）： 1733?1742.

[5] WIAUX Y， PUY G， VANDERGHEYNST P. Compressed sen?sing reconstruction of a string signal from interferometric observations of the cosmic microwave background [J]. Monthly notices of the Royal Astronomical Society， 2010， 402（4）： 2626?2636.

[6] WENGER S， MAGNOR M， PIHLSTR?M Y， et al. SparseRI： a compressed sensing framework for aperture synthesis imaging in radio astronomy [J]. Publications of the Astronomical Society of the Pacific， 2010， 122（897）： 1367?1374.

[7] LI F， BROWN S， CORNWELL T J， et al. The application of compressive sampling to radio astronomy： II. Faraday rotation measure synthesis [J]. Astronomy & astrophysics， 2012， 531（2）： 1261?1268.

[8] ONOSE A， CARRILLO R E， REPETTT A， et al. Scalable splitting algorithms for big?data interferometric imaging in the SKA era [J]. Monthly notices of the Royal Astronomical Society， 2016， 462（4）： 4314?4335.

[9] KOMODAKIS N， PESQUET J C. Playing with duality： an overview of recent primal?dual approaches for solving large?scale optimization problems [J]. IEEE signal processing magazine， 2015， 32（6）： 31?54.

[10] CHEN Shaoli， YANG Min. An adaptive fast iterative shrin?kage threshold algorithm [C]// 2017 29th Chinese Control and Decision Conference （CCDC）. Chongqing， China： IEEE， 2017： 2190?2194.

[11] ZIBETTI M V W， HELOU E S， PIPA D R. Accelerating over?relaxed and monotone fast iterative shrinkage?thresholding algorithms with line search for sparse reconstructions [J]. IEEE transactions on image processing， 2017， 26（7）： 3569?3578.

[12] ZHANG Songjie， MA Yuliang， ZHANG Qizhong， et al. Motor imagery electroencephalogram de?noising method based on EEMD and improved wavelet threshold [C]// 2018 Chinese Control And Decision Conference （CCDC）. Shenyang， China： IEEE， 2018： 5589?5594.

[13] 易清明，陈明敏，石敏.一种改进的小波去噪方法在红外图像中应用[J].计算机工程与应用，2016，52（1）：173?177.

[14] CARRILLO R E， MCEWEN J D， WIAUX Y. Sparsity avera?ging reweighted analysis （SARA）： a novel algorithm for radio?interferometric imaging [J]. Monthly notices of the Royal Astronomical Society， 2012， 426（2）： 1223?1234.