一种声学测试弹着点坐标的稳健估计方法

王玉龙 卢小汐 张亚辉 李宏凯 苏磊

摘  要： 针对火炮弹着点声检靶系统中弹丸着靶坐标精度不稳定的问题，建立抗差最小二乘法。该方法通过等价权函数将抗差估计与最小二乘法结合起来，利用残差对异常值进行降权处理，从而消除异常值对精度的不良影响。最后，对火炮弹着点声检靶系统进行仿真分析。分析和试验表明，抗差最小二乘法对异常值是稳健的，且精度优于一般最小二乘法，当靶幅为10 m×10 m且风速测试误差为3 m/s时，火炮弹着点声检靶系统针对火炮弹丸弹着点坐标测试精度优于5 cm。

关键词： 弹着点坐标; 稳健估计; 抗差最小二乘法; 抗差估计; 残差变化; 声定位

中图分类号： TN911.1?34; TJ306                   文献标识码： A                    文章编号： 1004?373X（2020）09?0025?04

A robust estimation method of acoustic test for impact point coordinate

WANG Yulong， LU Xiaoxi， ZHANG Yahui， LI Hongkai， SU Lei

（Huayin Ordnance Test Center， Huayin 714200， China）

Abstract： A robustified least square method is established for the instability coordinate precision of the sound detection target system for the projectile impact point. In the method， the robust estimation is combined with the least square method by the equivalent weight function， and the residual is used to reduce the weight of the outliers to eliminate the adverse effects of the outliers on the accuracy. The simulation analysis of sound detection target system for the projectile impact point was carried out. The analysis and test results show that the robustified least square method is robust to outliers and its accuracy is higher than that obtained with the general least square method. When the target area is 10 m×10 m and the measurement error of wind speed is 3 m/s， the tested coordinate accuracy of the impact point obtained with the sound detection target system for projectile impact point is within 5 cm.

Keywords： impact point coordinate; robust estimation; robustified least square method; robust estimation; residual variation; acoustic positioning

0  引  言

聲学立靶弹着点测试法属于基于到达时间差的无源定位，一般可得到一组非线性双曲方程组。一般采用最小二乘法（Least Square，LS）进行求解[1?3]。在弹着点声学靶系统试验测试过程中发现，有时传感器测量的时差存在粗差，即异常值或野值。由于测试系统中每个传感器所处位置不同，根据其测试波形处理得到的波达时刻也不同，很难从表面上区分哪些测试数据属于异常值或野值。在采用最小二乘法确定着靶坐标时，因为最小二乘法对异常值的敏感性，使得系统测试精度变低。

本文将抗差估计[4?5]与最小二乘法结合，建立了稳健估计方法（Robust Least Square，RLS），消除了异常值对定位结果精度的影响，且计算流程与最小二乘法一致。最后，给出了仿真与试验结果。

1  定位原理

声学靶系统主要采用传声器阵列，采集超音速弹丸产生的激波信号，再根据传声器坐标与激波时间差，确定弹丸通过空中虚拟平面的坐标。声学靶及立靶坐标系示意图如图1所示。其中，传声器采用双圆环布阵，每个圆环上均匀分布12个传声器，[xz]平面为水平面，[z]轴指向炮口方向，[xy]平面为竖直平面，[xy]平面即为虚拟靶平面，双圆环阵列位于靶平面内。

计算分析和实验表明，风对定位精度的影响不可忽略。假定风平行地面运动，且在弹丸着靶时刻靶面周围的局部风场是均匀的。因为风在[z]方向的分量[vz]影响较小[6?8]，所以主要考虑风在[x]方向的分量[vx]。利用矢量叠加原理可得到定位方程组如下：

[（x1-x-vx（t0+t1））2+（y1-y）2=v0（t0+t1）（x2-x-vx（t0+t2））2+（y2-y）2=v0（t0+t2）                                                 ?（xn-x-vx（t0+tn））2+（yn-y）2=v0（t0+tn）] （1）

式中：[ti，i=1，2，…，n]是激波到达各个传感器的相对时间（即时延或时差）;[t0]是激波视速度在靶面上传播至首先触发传感器的时间;[v0]是视速度。

方程组（1）中的未知参量为[x，y，v0，t0]。当[n≥4]时方程组（1）有解;当[n=4]时，方程组（1）是非线性方程组;[n>4]时，方程组（1）是超定非线性方程组（矛盾方程组）。求解方程组（1）即得[x，y，v0，t0]。

2  弹着点稳健估计方法

2.1  迭代公式

最小二乘法理论完善，算法成熟，得到了广泛应用。但是，当观测数据含有粗差（或异常值）时，经典最小二乘法的结果可能因异常值的存在而不可靠。在声靶试验过程中，由于传感器偶然抖动、风吹等不确定因素的影响，传感器测量的时差有时会出现异常值。此时，应用最小二乘法计算时，导致着靶测试精度低。稳健估计（也叫抗差估计）是指在存在异常值的情况下，通过选择适当的估计方法，使估计结果尽可能少地受到异常值干扰。稳健估计的原则是充分利用有效信息，限制利用可用信息，排除有害信息。

抗差最小二乘法通过等价权将抗差估计与最小二乘法结合起来，其实质是等价权函数的设计。当实测时差不含异常值时，抗差最小二乘法的结果与最小二乘法结果一致;当实测时差含有异常值时，抗差最小二乘法能够消除异常值的影响。

下面详细推导抗差最小二乘法的迭代公式，记：

[fi=（x-xi+vx（t0+ti））2+（y-yi）2-v20（ti+t0）2，                             i=1，2，…，n]   （2）

设[f： D?R4→Rn]，[f=（f1，f2，…，fn）T]。求解非线性方程组（1）等价于求解如下非线性最小二乘问题。

[minx∈D12fT（x）f（x）]   （3）

利用Taylor级数展开将非线性问题转化为线性问题，在[x0=（x0，y0，v00，t00）]展开得：

[f（x0）+DfT（x0）（x-x0）=0]   （4）

式中：[Df（x0）=Df1DxDf1DyDf1Dv0Df1Dt0Df2DxDf2DyDf2Dv0Df2Dt0????DfnDxDfnDyDfnDv0DfnDt0x0]是Jacobi矩阵;[DfiDx=2（x-xi+vx（t0+ti））];[DfiDy=2（y-yi）];[DfiDv0=][-2v0（ti+t0）2];[DfiDt0=-2v20（ti+t0）];[i=1，2，…，n]。

记[b=-f（x0）]，[A=DfT（x0）]，[X=（x-x0）]，则：

[AX=b] （5）

进而，有：[x1=x0+（ATP0A）-1ATP0b]。

一般地，抗差最小二乘迭代公式如下：

[xk+1=xk+（ATkPkAk）-1ATkPkbk，k=0，1，2，…] （6）

式中[Pk]称为等价权矩阵或等价权函数。特别地，当取[Pk=I]时，抗差最小二乘法退化为最小二乘法。

就数学表达式而言，抗差最小二乘法与加权最小二乘法基本相同，其区别是权函数的内容不同。加权最小二乘法的权是先验的，而抗差最小二乘法的权是残差的函数。

2.2  等价权矩阵的确定

权函数的作用在于：将所有的观测数据划分为正常观测值、可利用观测值和粗差观测值（异常值）三个部分。对于正常观测值，使其保持原有的权不变，对余差较大的可利用观测值进行降权处理，而那些粗差观测值，则使其权为零。经过这样的处理，就可以根据各个观测值及“后验权”，求得最接近于正常情况下的结果。本文中权函数选为IGGⅢ权函数（IGG是中国科学院测量与地球物理研究所的英文缩写），其表达式如下：

[Pi（vi）=1，    vi≤k0k0vik1-vik1-k02，    k0k1] （7）

式中：[vi=δiσ]，[δi=fi]是残差，[σ]是标准化残差，[σ=i=1nδi（n-1）]，[k0∈（1，1.5）]，[k1∈（2.5，8.0）]，本文取[k0=1.5]，[k1=3]。

IGGⅢ权函数充分考虑了正常阶段、可疑階段和淘汰阶段三个部分，公式简单，易于实现，如图2所示。

2.3  算法流程图

抗差最小二乘法的计算流程如图3所示。

2.4  等价权和残差变化的算例

以某型榴弹试验为例进行分析，图4给出了迭代过程中不同传感器对应的残差和等价权，其中横坐标代表传感器编号，纵坐标分别代表残差、标准化残差和等价权。

由图4可知，在迭代的过程中，有多个传声器的等价权发生变化，随着迭代的不断进行，最后6号传声器的等价权减小，并降为0，即最终判断6号传感器存在异常。图5给出了对应的弹着点误差随迭代次数的变化曲线。

由图5可知，随着迭代次数的增加，水平误差基本不变，而高低误差由42.3 cm降低到1.0 cm，即抗差最小二乘法消除了异常值的影响。

3  仿真分析

影响声学靶测量误差的因素主要有：传感器坐标测试误差、传感器时延误差、温度测试误差和风速测试误差。传感器坐标测试误差和时延误差由设备决定，温度变化比较稳定。声靶计算修正时用到的环境风速是激波在靶面附近传播几毫秒间的瞬态风速，测试误差较大。下面以靶幅10 m×10 m，传感器坐标测试误差为1 mm，传感器时延误差为5 μs，温度测试误差为5 ℃，风速测试误差分别为1 m/s，2 m/s，3 m/s和4 m/s时，给出误差分布图，如图6，图7所示。

由图6和图7知，随着风速测试误差的增加，水平误差和高低误差也随之增加。表1给出了在不同风速测试误差时的均方根误差。

4  试验数据结果与分析

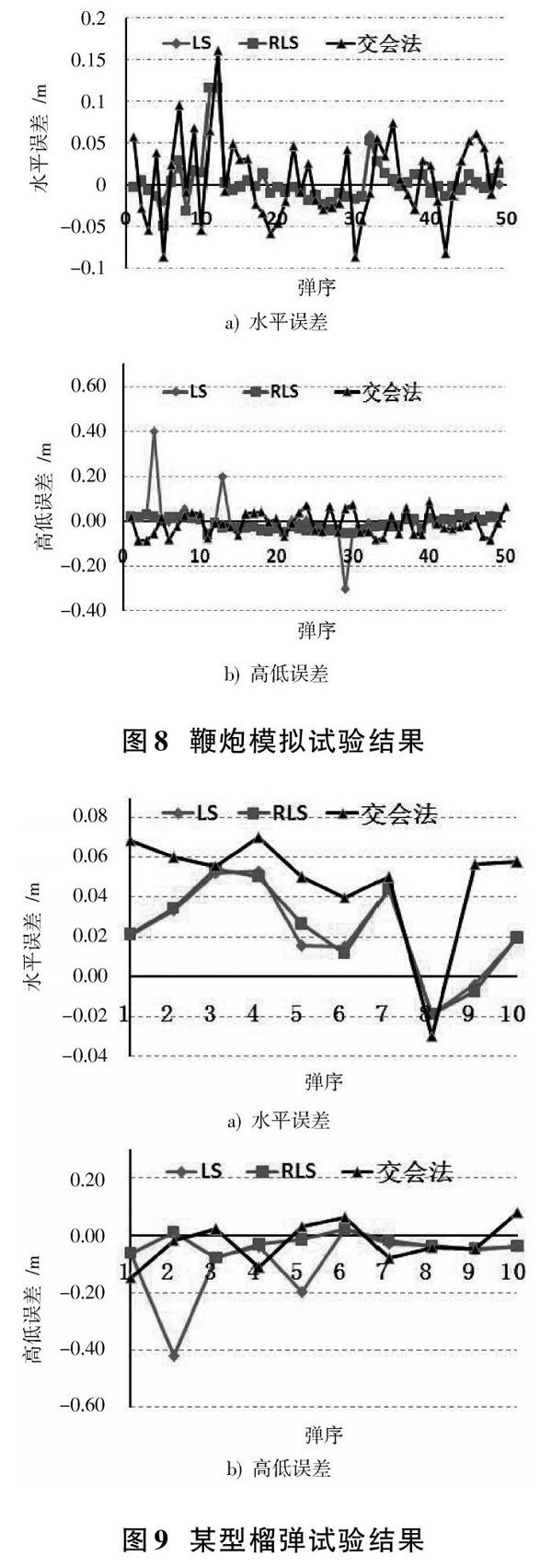
4.1  鞭炮模拟试验

采用鞭炮爆炸激发传声器，事先测量出鞭炮炸点和传声器的相对关系，作为真值，检测声学靶的精度。分别采用LS法、RLS法和交会法进行计算，对比不同算法的精度。其中，交会法采用文献[8]中的交会计算方法。试验结果如图8所示。

由图8可知，交会法的水平均方根误差为5.0 cm，高低均方根误差为6.0 cm;LS法的水平均方根误差为2.8 cm，高低均方根误差为8.1 cm;RLS法的水平均方根误差为2.8 cm，高低均方根误差为2.9 cm。从而可知，LS法容易受到异常值的影响，而RLS法能够保证测量的稳健性，并且RLS法的精度优于交会法。

4.2  某型榴弹试验

某型榴弹试验同样分别采用LS法、RLS法和交会法进行计算，对比不同算法的精度。结果如图9所示。

由图9知，交会法的水平均方根误差为5.5 cm，高低均方根误差为7.6 cm;LS法的水平均方根误差为3.2 cm，高低均方根误差为15.4 cm;RLS法的水平均方根误差为3.3 cm，高低均方根误差为4.5 cm。与鞭炮模拟试验结果类似，RLS法精度最高。

5  結  论

本文针对火炮弹着点声学靶系统定位计算方法进行研究，建立了基于抗差最小二乘法的稳健估计方法，提高了弹丸着靶坐标的测试精度。对火炮弹着点声学靶系统进行仿真分析，风速测试误差越大，着靶坐标测试精度越低。当风速测试误差为3 m/s时，着靶坐标测试精度为5 cm。

参考文献

[1] 王磊，陈昭男.基于被动声学的超声速武器脱靶量解算方法[J].应用声学，2018，37（3）：385?390.

[2] 苗晟，周维，唐浩，等.一种声源定位系统设计[J].计算机科学，2013，40（11A）：398?400.

[3] 刘哲，陈日林，滕鹏晓，等.基于平面传声器阵列的声源定位系统[J].声学技术，2011，30（2）：123?128.

[4] 张洋，张志刚，钱栋，等.基于IGGⅢ模型的高精度抗差坐标转换算法研究[J].全球定位系统，2017，42（5）：29?32.

[5] 李蝉，张士峰，张力军.应用抗差无迹卡尔曼滤波的再入弹道处理技术[J].国防科技大学学报，2017，39（1）：1?5.

[6] MSI. Strafe scoring target type 590 air?to?ground training [EB/OL]. [2014?07?20]. http：//www.msinstruments.com.

[7] 蒋东东，狄长安.八点线式声学立靶弹着点检测系统研究[J].电子测量技术，2010，33（4）：19?21.

[8] 冯斌，石秀华.双三角阵声靶测试系统研究[J].应用声学，2012，31（2）：140?144.

[9] 董杰，高楼.弹丸任意角度入射弹着点声学检测模型[J].计算机仿真，2015，32（1）：10?14.