等堆积效率条件下水层厚度对浆体特性变化影响
徐志强,郑剑平,李凡飞,王 磊,涂亚楠
(1.中国矿业大学(北京) 化学与环境工程学院,北京 100083;2.教育部煤基浆体燃料工程研究中心,北京 100083)
近年来,我国能源安全形势变得日益严峻,煤炭资源作为当前我国主要能源,其清洁高效利用至关重要。水煤浆技术作为煤炭清洁高效利用技术之一,在一定程度上得到了很大的发展。目前,水煤浆主要应用于东南沿海区域的中小型工业锅炉、陶瓷等建材领域中的喷雾干燥塔的燃料和现代煤化工领域作为德士古气化炉的原料[1],应用广泛。但如何制备出高浓度水煤浆,高效率地利用煤炭资源显得尤为重要。
水煤浆的制备过程中,有效地控制好颗粒的粒度分布,形成良好的粒度级配,可制得高浓度浆体。不同粒度分布一般堆积效率也会不同,其对水煤浆的可制浆浓度、流变性和稳定性等产生重要影响[2]。一般而言,堆积效率越高,可制浆浓度越高,稳定性越好[3]。但对于等堆积效率而不同粒度分布条件下,水煤浆制浆浓度和稳定性的变化规律方面却未见相似研究。
本文提出了一种颗粒外围水层厚度的概念和相应理论计算方法,并探讨了相同堆积效率、不同粒度分布条件下,水煤浆的可制浆浓度与稳定性随着颗粒外围水层厚度的变化规律。
1 模型建立
在张荣曾提出的隔层堆积理论模型[2]及Tu等提出的颗粒堆积效果评价指标E的计算方法[3]等的研究基础上,提出了水煤浆体系中煤颗粒外围水层厚度的计算模型。
1.1 颗粒外围水层厚度的定义
在水煤浆体系中,颗粒与颗粒间不直接接触,两个颗粒的表面之间存在一层水。单就某个颗粒而言,其外围水层厚度被认为是中间层的一半,记为L。显然L值与水煤浆浓度直接相关,如图1所示。

图1 颗粒外围水层厚度L的示意图
1.2 假设
参照Tu提出的堆积效果评价指标E的计算模型假设[3],本模型的假设如下:
1)均匀性假设——在水煤浆体系中,煤颗粒是均匀分布的。
2)离散型假设——整个水煤浆体系可以划分为有限数量的计算微元结构,且每个结构中的颗粒粒径分布完全一致,且具有相同的堆积模式和堆积效率。
3)可变形假设——计算微元可以发生变形、重组,甚至可以分割为数量不限的更小结构离散到整个体系,但在计算中仍被认为是同一个微元的内部元素。
4)平均性假设——在同一个水煤浆体系中,所有颗粒的L值均相等。
5)堆积模式一致性假设——忽略因粒度效应对不同大小颗粒表面水层厚度的影响,且水层厚度无论多大或多小均不对颗粒堆积体系膨胀或压缩有任何干扰。
1.3 建模计算
首先参照Tu提出的堆积效果评价指标E的计算模型[3],使用同样的方法计算E值。
而对于任一颗粒,当外围形成水层后,其体积将发生膨胀。显然,不同粒径颗粒的膨胀率是不同的。如图1所示,由于有水的存在,可认为每个颗粒均增加了一层外围水层,其粒径将增大2L。
对于任一i级次级粒级,其平均粒径di因外层有水层后的平均粒径Di为:Di=di+2L。则相应的体积膨胀率φi为:
此时,以膨胀后的窄粒级固体颗粒体积作为实际体积替换Tu的方法中的窄粒级固体颗粒体积进行相似计算。据上述总表观体积,并利用颗粒体积、颗粒视密度、颗粒真密度、水的密度等参数,就可以计算出颗粒体积增大2L后的体系的固体颗粒质量浓度,或者就是水煤浆的计算浓度。显然,这个计算过程无法给出确定的L值。因此具体的计算操作是,先给定L一个小值,并以更小的增量ΔL进行反复计算,直至水煤浆计算浓度值恰好超过实测浓度值时,将此值及前一个值做平均,即可得到相对准确的L值。其准确性可以由增量ΔL的大小来确定,本文中采用0.01μm。
2 煤样性质与研究方法
2.1 煤样性质
煤样来自于神东集团哈拉沟选煤厂神优2号产品,其工业分析与元素分析见表1。
由1.3节计算过程解释可知,为了较为准确计算各煤样制备的水煤浆的L值,需要测试煤样的真密度、孔隙率,本文参照真密度测试国家标准检测煤样的真密度及采用压汞法测试煤样的孔隙率,并计算出内在水分,测量结果见表2。

表1 煤样煤质分析结果 %

表2 煤样的密度、孔隙率和内水
2.2 研究方法
研究选取亚甲基二萘磺酸钠(NNO)作为制浆用分散剂,其最佳用量经预试验确定为干煤质量的0.8%。样品处理方法为:将收到的煤样在空气中进行干燥2~3d,制成实验所需的空气干燥基。将空气干燥基煤样(>100kg),拣出大块矸石后,然后按照GB/T 474—2008经过小型颚式破碎机破碎至3mm以下过筛后,利用二分器进行混合、缩分至10kg,用样品袋真空封存,存放在阴凉处。其余煤样送入球磨机中进行磨制,控制不同的研磨时间后,用电动振筛机过0.3mm筛子,筛上物料再投入球磨机研磨,最终制取0.3mm以下煤粒封存于样品袋中并标记好。研磨时间根据其物料粒度分布(采用OMIC LS-C(I)型激光粒度分析仪测试粒度分布)进行控制,以得到煤样的粗样、细样、超细样三种样品(CS、FS、CFS),作为配置不同粒度分布的制浆样品。由此得到的粒度分布如图2所示。
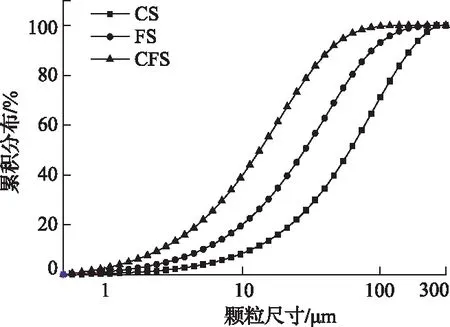
图2 煤样粒度分布图
制浆方法为:将粗、细、超细样品按选定的配比准确称量,加入一定量的分散剂和水,使用高速搅拌器,在低转速条件下将煤粉、分散剂和水进行预先捏混4~5min,使煤样充分润湿,形成有一定流动性的混合物,然后进行高速搅拌混匀10min,搅拌速率为1000r/min,使煤颗粒与药剂间得到进一步熟化。粗、细及超细样品的配比依据E值相近、L值不同的原则进行遴选。最终CS∶FS∶CFS质量比为0∶5∶8、0∶5∶2、3∶8∶1、9∶9∶1,其E值分布在84.61±0.01%,见表3。

表3 不同配比下颗粒间堆积效率E和水层厚度L
煤浆特性检测方法:水煤浆浓度采用Sartorius MA35快速水分分析仪测试,表观粘度、切应力和剪切率等采用Brookfield DV2T型旋转粘度计测试,并依据Herschel-Bulkley模型[1,4-8]进行拟合。在此,定义可制浆浓度R值:在最优用药量、常温及剪切速率为100s-1条件下,水煤浆的表观粘度达到1000mPa·s时的浆体浓度。水煤浆稳定性采用Turbiscan Lab稳定性分析仪进行测试分析,观察15d静置后,析水率h和稳定性指标TSI值的变化规律[9-11]。
3 水层厚度L对浆体特性变化的影响
3.1 L值对可制浆浓度R的影响
不同L值下的可制浆浓度R如图3所示。可见,随着L值的增大(由最小值到最大值增大了约50%),R值也呈现增加趋势。也就是说,在堆积效率相近的条件下,适当增大L值将会提高制浆浓度。这主要是因为等堆积条件时,L值大的配比中粗颗粒含量占比大,相当于整体外表面积下降。此时若仍以等浓度且等堆积效率制备水煤浆时,L值大的配比的水煤浆体系中的自由水量相对L值小的配比要多一些,从而使粘度下降。故在可制浆浓度角度进行考察时,相应的制浆浓度会高一些。但由图3还可以发现,所有配比的可制浆浓度均分布在59.95±0.3%之间,在很窄的范围内变化。也就是说,尽管L值相对增大了约50%,但所对应研究的浓度值仅相对提高了约0.5%,浓度增大幅度很小。可见,在堆积效率相近的情况下,L值仅能在很有限的范围内对可制浆浓度进行调节,且满足L值越大,可制浆浓度越大。因此,图3也从侧面验证了,采用E值进行堆积效率和制浆过程的指导更为有效。
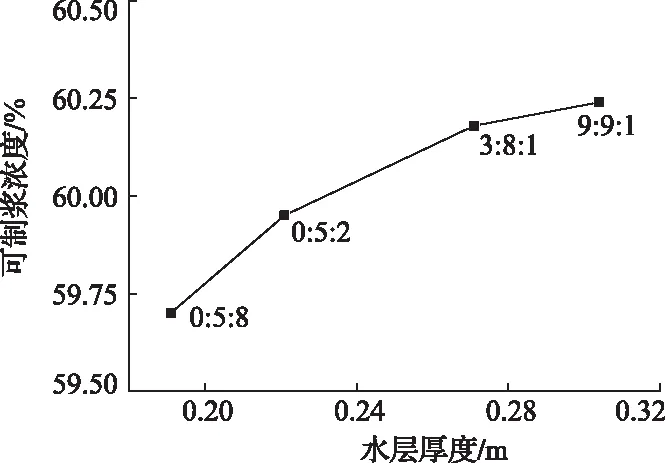
图3 R与L的关系
3.2 L值对水煤浆析水率h的影响
不同L值条件下,水煤浆经过静置15d后的析水率如图4所示。可见,颗粒外围水层厚度L值越大,静置15d后的析水率也越大。主要是因为四个配比的E值是近似相等的,即制备水煤浆的可制浆浓度也都是很相近的,水层厚度L越大,也就意味着体系中形成的煤、水、分散剂的三维空间结构中所包含的自由水含量就越多。随着静置时间的增加,原形成的三维稳定体系被慢慢破坏掉,失去稳定,将释放出自由水,且L值越大,释放出自由水量越多,即形成更厚顶部澄清层,析水率h也就更大。

图4 L与h之间的关系
3.3 L值对水煤浆稳定性指标TSI的影响
不同L值条件下,经Turbiscan Lab稳定性分析仪基于背散射光谱检测结果得到的水煤浆稳定性指标TSI值如图5所示。可见,在堆积效率相近的条件下,TSI值随着L值的增大而增大,即水煤浆稳定性变差。这主要是由于L值表征了复合颗粒(指含有外围水层的煤颗粒)间的距离,其值越高,表明颗粒受微观条件下的布朗运动引起的微剪切越强,可以自由移动的距离也就越大,从而不仅提供了更多的动能,也提供了更宽的可压缩移动范围,进而导致颗粒团聚并沉降的态势更高,使得水煤浆整体的稳定性变差。

图5 TSI与L的关系
4 结 论
1)等堆积效率下,颗粒整体较粗的煤所制备的水煤浆的水层更厚,其可制浆浓度更高,但提高的幅度很小,揭示了采用E值进行堆积效率和制浆过程的指导更为有效。
2)水层厚度越大,外围水层中的自由水含量也越多,颗粒的可移动范围也越大,颗粒受到微剪切的影响作用也就越显著,使得体系的析水率越大,稳定性指标TSI值越高,水煤浆趋于更不稳定。

