基于优势粗糙集的交通事故多属性关联分析

郭 庆

(合肥工业大学 数学学院,安徽 合肥 230601)

经典粗糙集模型[1-2]只能局限于分类问题而不能有效地处理分级决策问题。基于此原因,文献[3]提出了优势粗糙集模型,该模型主要以优势关系代替等价关系对决策等级类进行近似。近年来,很多学者针对优势粗糙集模型做了相应的改进并应用于多个领域[4-9]。交通事故指标分析方法主要包括专家评议法、层次分析法、模糊聚类、关联度分析、决策树分析、BP神经网络、Bayes网络等方法[10-13]。作为一种处理不精确、不确定与不完全数据的新的数学理论,粗糙集模型能在无先验知识并且没有事先对数据或知识进行主观评价的条件下,仅仅利用数据本身所包含的信息,就能够客观有效地对数据进行分析和处理。文献[14]通过事故多发点的统计数据建立了基于粗糙集理论的决策表,并对交通事故的影响因素的程度大小进行了分析;文献[15]构建了基于分辨矩阵的属性约简算法模型,并结合实测数据验证分析,提取出导致拥堵的关键因素;文献[16]研究了高速公路黑点成因分析,提出了一种基于粗糙集与模糊集的因素权重算法。

现有的研究都是基于等价关系并且只对单个决策属性的粗糙集模型进行分析,并未考虑交通事故指标的多元性及其指标值大小的比较。本文以交通事故指标为背景,从隐患指标和事故指标2个一级指标构造一种多决策属性优势粗糙集模型,分析其相关性质及其与单决策属性优势粗糙集模型的区别与联系,定义隐患指标相对于事故指标的分类质量,并基于分类质量给出指标的相对约简及其最简序决策规则的获取方法;最后结合具体的数据对模型进行验证。

1 优势粗糙集

在优势粗糙集模型中,有序的属性也称为准则,相应的信息系统称为序信息系统,对应的序关系通常分为优势关系与劣势关系。

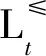
2 交通事故指标的粗糙集模型及其性质

交通事故数据可以用一个决策信息系统S=(U,C∪D,V,f)表示[13],其中,U表示论域,即所有待研究的交通事故数据集；C表示交通隐患指标集;D表示交通事故指标集。本文考虑多个事故指标的情形,设D={t(1),t(2),…,t(n)}表示所有的事故指标集,并且第i个事故指标t(i)下的序分类记为:

(1)

(2)

(3)

(4)

分别表示论域中在多个事故指标t(1),t(2),…,t(h)下的优势序分类集与劣势序分类集。

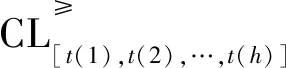
(5)

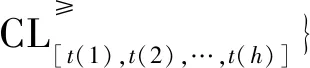
(6)

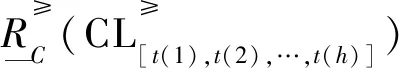
(7)

性质1 多个事故指标下优势序分类的上下近似集满足下列性质:

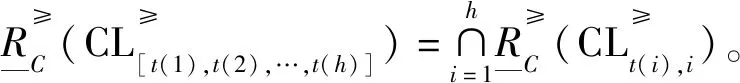
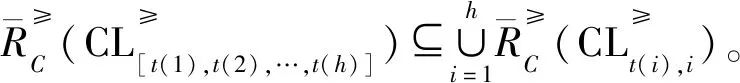
证明

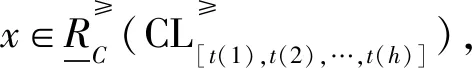
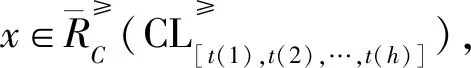
性质1揭示了优势关系下单个事故指标下的上下近似与多个事故指标下的上下近似之间的区别与联系;劣势关系的情形可类似得到,这里不再一一给出。

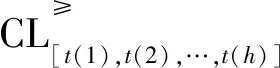
(8)

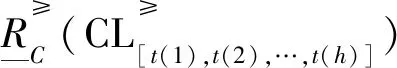
3 实例分析

为了验证模型的有效性,本文采用文献[10]中的部分数据见表1所列,其中,ai表示所研究的对象；隐患指标包括如下7个指标:r1表示城镇化水平,r2表示道路交通网密度,r3表示千人均车辆保有量,r4表示恶劣天气比例,r5表示交通违法率,r6表示驾驶员技术的平均水平,r7表示道路管控的水平；事故指标包括如下3个指标:d1表示事故的致死率,d2表示交通事故的死亡率,d3表示万辆机动车引发的死亡率。表中各项指标的详细意义可参考文献[10]。

表1 道路交通安全指标原始数据

首先对表1进行数据预处理[10],即对各个指标进行量化等级,具体如下:

r1:[45,50)为1级,[50,55)为2级,[55,60)为3级,[60,65)为4级,[65,70)为5级;

r2:[1.5,2)为1级,[1.2,1.5)为2级,[1,1.2)为3级,[0.8,1)为4级,[0,0.8)为5级;

r3:[225,300)为1级,[200,225)为2级,[175,200)为3级,[150,175)为4级,[0,150)为5级;

r4:[0,30)为1级,[30,35)为2级,[35,40)为3级,[40,45)为4级,[45,50)为5级;

r5:[0,2)为1级,[2,4)为2级,[4,6)为3级,[6,8)为4级,[8,10)为5级；

r6:[8,10)为1级,[6,8)为2级,[4,6)为3级,[2,4)为4级,[0,2)为5级;

r7:[20,30)为1级,[15,20)为2级,[10,15)为3级,[5,10)为4级,[0,5)为5级。

d1:[10,14)为1级,[14,18)为2级,[18,22)为3级,[22,26)为4级,[26,30)为5 级;

d2:[0,0.2)为1级,[0.2,0.25)为2级,[0.25,0.3)为3级,[0.3,0.4)为4级,[0.4,0.5)为5级;

d3:[0,2)为1级,[2,5)为2级,[5,10)为3级,[10,15)为4级,[15,20)为5级。

其中,1级表示非常安全;2级表示较安全；3级表示安全;4级表示较不安全;5级表示不安全。根据上述量化等级,将表1转化，见表2所列。

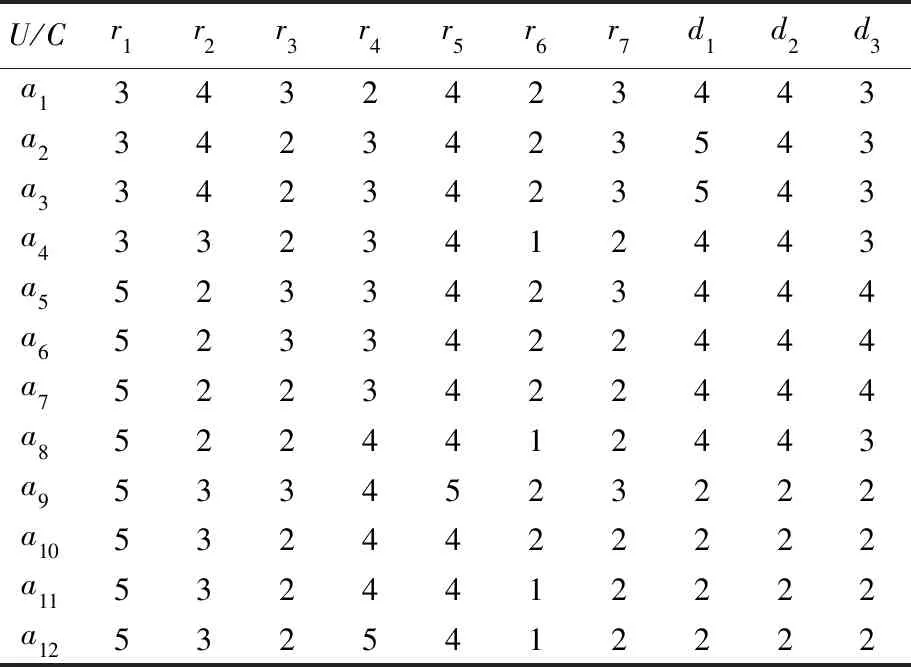
表2 量化等级后的指标数据

由(5)式和(6)式可得到如下计算结果:

由(8)式得:

于是可得4个相对隐患指标约简集:

R1={r1,r2,r4,r5,r6,r7},

R2={r1,r2,r3,r4,r6,r7},

R3={r1,r2,r3,r4,r5,r7},

R4={r1,r2,r3,r4,r5,r6}。

根据下近似集中的对象可获取下列确定性序决策规则:

规则1:若r1≥3∧r2≥4∧r4≥2∧r5≥4∧r6≥2∧r7≥3,则d1≥4∧d2≥4∧d3≥3。

规则2:若r1≥3∧r2≥4∧r4≥3∧r5≥4∧r6≥2∧r7≥3,则d1≥4∧d2≥4∧d3≥3。

规则3:若r1≥3∧r2≥4∧r4≥3∧r5≥4∧r6≥2∧r7≥3,则d1≥5∧d2≥4∧d3≥3。

规则4:若r1≥3∧r2≥4∧r3≥3∧r4≥2∧r6≥2∧r7≥3,则d1≥4∧d2≥4∧d3≥3。

规则5:若r1≥3∧r2≥4∧r3≥2∧r4≥3∧r6≥2∧r7≥3,则d1≥5∧d2≥4∧d3≥3。

规则6:若r1≥3∧r2≥4∧r3≥3∧r4≥2∧r5≥4∧r7≥3,则d1≥4∧d2≥4∧d3≥3。

规则7:若r1≥3∧r2≥4∧r3≥2∧r4≥3∧r5≥4∧r7≥3,则d1≥5∧d2≥4∧d3≥3。

规则8:若r1≥3∧r2≥4∧r3≥3∧r4≥2∧r5≥4∧r6≥2,则d1≥4∧d2≥4∧d3≥3。

规则9:若r1≥3∧r2≥4∧r3≥2∧r4≥3∧r5≥4∧r7≥2,则d1≥5∧d2≥4∧d3≥3。

可能性序决策规则可由边界集中的对象类似得到,这里不再一一给出。

基于相关系数,文献[10]给出单个隐患指标与单个事故指标之间的正负相关计算结果,但未体现隐患指标与事故指标间的整体关联性。

本文基于多决策属性的优势粗糙集模型直接面向具体数据表,消去冗余的隐患指标,并获取多个交通隐患指标与多个事故指标间的序决策规则,且计算方便。以决策规则1为例,如果该地区城镇化水平高于3级,道路交通网密度高于4级,恶劣天气比例高于2级,交通违法率高于4级,驾驶员技术的平均水平高于2级,且道路管控的水平高于3级,那么该地区交通事故的致死率高于4级,交通事故的死亡率高于4级,且万辆机动车引发的死亡率高于3级。

4 结 论

现有交通事故指标分析的粗糙集模型不能有效处理多个决策属性的情形。本文面向交通事故指标数据,分别从隐患指标和事故指标2个一级指标,构造了一种多决策属性优势粗糙集模型,分析了其相关性质及其与单决策属性优势粗糙集模型的区别与联系,定义了隐患指标相对于事故指标的分类质量,给出了隐患指标相对于事故指标的相对约简的求解及其序最简决策规则的获取方法,结合具体的数据对模型进行了验证,拓展了粗糙集理论在交通事故指标关联分析中的应用。