基于多光伏互补模型的最优出力设定值算法

薛 婧,董王朝

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

光伏发电受自然气候因素影响,具有很大的不确定性。在大规模光伏并网条件下,为保证系统的可靠性,一方面令光伏电站运行于降额状态,限电弃光;另一方面需要额外安排一定容量的备用,以响应光伏出力随机波动,维持电力系统功率平衡[1]。互补模型可利用光伏电站出力的空间分布不均匀性,对多个光伏电站组成的联合系统实现统一调度,在满足供电安全约束的条件下,降低联合系统的备用需求,进而降低电网的运行成本。

现有研究关于互补模型在电力系统中的应用,多集中在风光互补[2-4]、风水互补[5-6]、风光储互补[7]等领域。文献[2]提出了光伏电站和风电场互补出力调度策略;文献[3]提出了风光荷联合概率密度函数,将光伏、风电与负荷的概率分布相结合;文献[4]提出了改进的拉格朗日分解法求解风光互补优化模型;文献[5]通过在风电场与水电站间建设高压直流输电线路的方式来改进互补系统出力平稳性;文献[6]建立了充分利用清洁能源的风水火发电系统多目标优化模型;文献[7]提出一种风光储混合系统的容量优化方法,考虑了并网与离网2种运行方式;文献[8]提出在光伏市电互补系统结构的基础上,提出一种功率自动分配方法;文献[9]提出了适用于2个风电场的互补备用控制策略,但在扩展到多个风场的情况时遇到困难。对于部分区域电网,不一定同时接入多种可再生能源,或不同可再生能源容量相差较大,多种能源互补无法实现。以合肥电网为例,新能源以光伏为主,而风电并网较少。此外,随全球能源互联网的发展,有可能实现光伏功率的跨时区输送,不同区域电网的光伏功率可以互为备用。因此,有必要研究单一类型可再生能源的互补模型,如多光伏电站间的功率互补。

关于多光伏电站互补的研究较少。文献[10]考虑光伏出力相关性,改进出力序列生成方法;文献[11]研究多光伏电站对概率潮流的影响;文献[12]利用多点线性近似方法,提高含光伏配网概率潮流的精度;文献[13]考虑同一区域内光伏出力强相关性对无功优化的影响;文献[14]从可靠性的角度出发,研究光伏出力波动与相关性,评估光伏发电置信容量。现有研究不曾涉及利用多光伏电站间出力相关性降低备用的需求,也没有给出光伏电站出力设定值的计算方法。

现有方法[15]确定备用需求,常采用预测误差标准差的固定比例。此类确定性方法从经济性和可靠性角度来看并非最优。而概率方法一般假设预测误差服从特定概率分布,以备用在一定置信水平下大于预测误差确定备用需求,其中以正态分布最为常用[16-17]。但也有研究表明,采用正态分布拟合光伏预测误差不符合实际情况[18];文献[19]采用Weibull分布描述光照强度的不确定性;文献[20]认为Beta分布描述非对称性具有优势,但对多峰分布的描述存在不足。混合高斯模型(Gaussian mixture model,GMM)[21-22]不局限于特定概率密度函数形式假设,使用若干高斯密度函数的线性组合逼近非正态密度函数,可用于建立光伏出力预测误差的分布模型。

本文提出考虑备用约束的多光伏电站互补模型,针对互补模型中,光伏出力设定值取值困难的问题,提出差分进化算法结合内点法求解最优出力设定值。采用差分进化算法对各个光伏电站的出力设定值进行随机寻优,以充分利用光伏发电为目标,以备用容量满足供电安全置信度为约束条件。获得最优出力设定值之后,将其带入多光伏电站互补模型中,求解各光伏电站各时段调整后的有功出力以及备用容量需求。

1 多光伏电站互补模型

1.1 光伏电站互补策略

本文提出改进的多光伏电站互补模型,其效果为使得各光伏出力之和接近于设定值之和而不大于设定值之和。在给定时段内,若某个光伏电站可用出力相对于出力设定值有余量,该余量可用于补偿其他光伏电站出力相对于出力设定值的不足。同时,降额运行也降低了多光伏电站联合系统对于备用的需求。该模型可以满足多光伏电站、多时段的调度要求。目标函数如下:

(1)

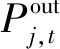
约束条件如下:

(2)

1.2 备用需求分析

光伏电站的备用容量需求与预测误差ew有关。不考虑互补模型,备用容量应当在一定的置信水平α下,满足出力计划,即

(3)

考虑多光伏电站互补,要求备用容量在同样置信水平下,满足出力计划,即

(4)

对比(3)式、(4)式可知,考虑互补之后,光伏电站不再根据预测出力制定出力计划与备用计划,以出力设定值作为运行参考。且(3)式、(4)式中,只有ew为随机变量,已知分布即可计算概率。引入GMM方法[21],估计光伏出力预测误差的概率密度函数(probability density function,PDF)。同时考虑光伏出力波动较大,对不同时刻的预测误差分别建模。GMM的PDF可表示为:

(5)

其中,ai为权重系数;μi为均值;σi为标准差;N(Xi;μiσi)为第i个高斯分量的分布函数。GMM参数可采用最大似然估计法获取。

2 最优出力设定值算法

采用互补模型调整出力,首先要确定每个光伏电站的出力设定值。考虑到单个光伏电站的实时出力与出力设定值有关,而该光伏电站所需的备用容量又与其实时出力有关。若要确定光伏电站的最优出力设定值,则可通过差分进化(differential evolution,DE)算法对设定值进行随机寻优,最优出力设定值算法实际上完成了多光伏电站互补模型的参数确定。

引入DE算法随机搜索各个光伏电站的出力设定值,将随机生成的出力设定值带入多光伏电站互补模型中,采用内点法进行求解。求解时,应满足光伏电站备用安全约束,以充分利用光伏发电为目标,得到各个光伏电站的出力设定值以及各时段备用容量需求。当该光伏电站在出力设定值之下时,配合备用,可以满足要求的供电可靠性。计算步骤如下:

(1) 设置DE算法种群规模、缩放因子与交叉概率。

(2) 初始化种群。种群中每个个体都是最优出力设定值的一组解,第k代种群可表示为:

(6)

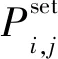
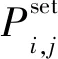
(7)

(3) 对每个个体采用内点法求解最优备用。将(1)式、(2)式引入松弛变量s1,t、s2,t与拉格朗日乘子yt、zt,由目标函数转化得拉格朗日函数L,即

(8)

令拉格朗日函数对所有变量及乘子的偏导为0,得到:

(9)

(9)式为多光伏电站互补模型的KKT方程组，求解(9)式,可得对应出力设定值组合下的光伏电站有功出力,进一步根据(4)式、(5)式计算各光伏电站的备用容量需求。

(4) 评估每个个体的总社会效益TCB,即

(10)

其中中,Cj,t、Bj,t分别为光伏发电效益与备用成本。

(11)

其中,缩放算子F∈[0,2],起放大控制偏差变量的作用。光伏电站并不需要太过精确的设定值,缩放因子F取值为1。

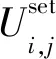
(12)

其中,rand(i)为产生(0,1)之间随机数发生器的第i个估计值,randn(i)∈{1,2,…,D}序列中随机选择的一个整数,用它来确定至少从变异种群获得一个参数;CR为交叉概率,取值范围为[0,1]。

(8) 选择。按照贪婪准则将每个测试个体与种群中的对应个体进行比较,总社会效益高的个体进入下一代种群。

(9)k=k+1,如果没有超过最大值,那么转步骤(5)。

(10) 输出最优主力设定值组合,及所需的备用容量。

算法流程如图1所示。

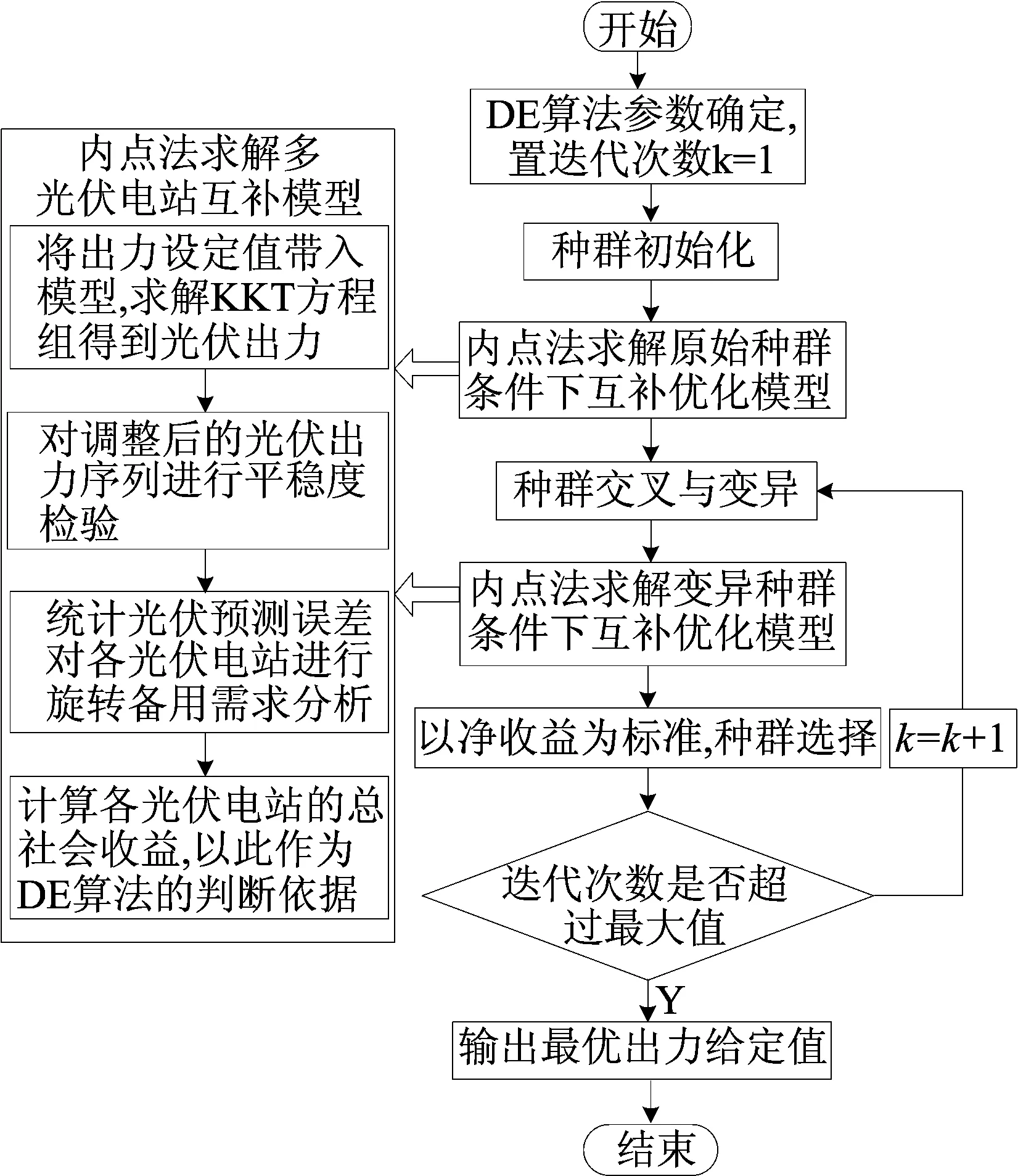
图1 最优出力设定值算法流程

3 算例分析

采用比利时Elia电力公司[23]的历史数据,将安特卫普、列日、西佛兰德3个地区的光伏出力视为3个光伏电站,装机容量为535.19、371.93、478.36 MW。设光伏出力收益与备用成本分别为200、300 美元/MW,取光伏电站供电安全置信水平α=0.90。

以13时段为例,采用GMM方法建立该时段的光伏出力预测误差的PDF,并与经验结果对比,结果如图2所示。

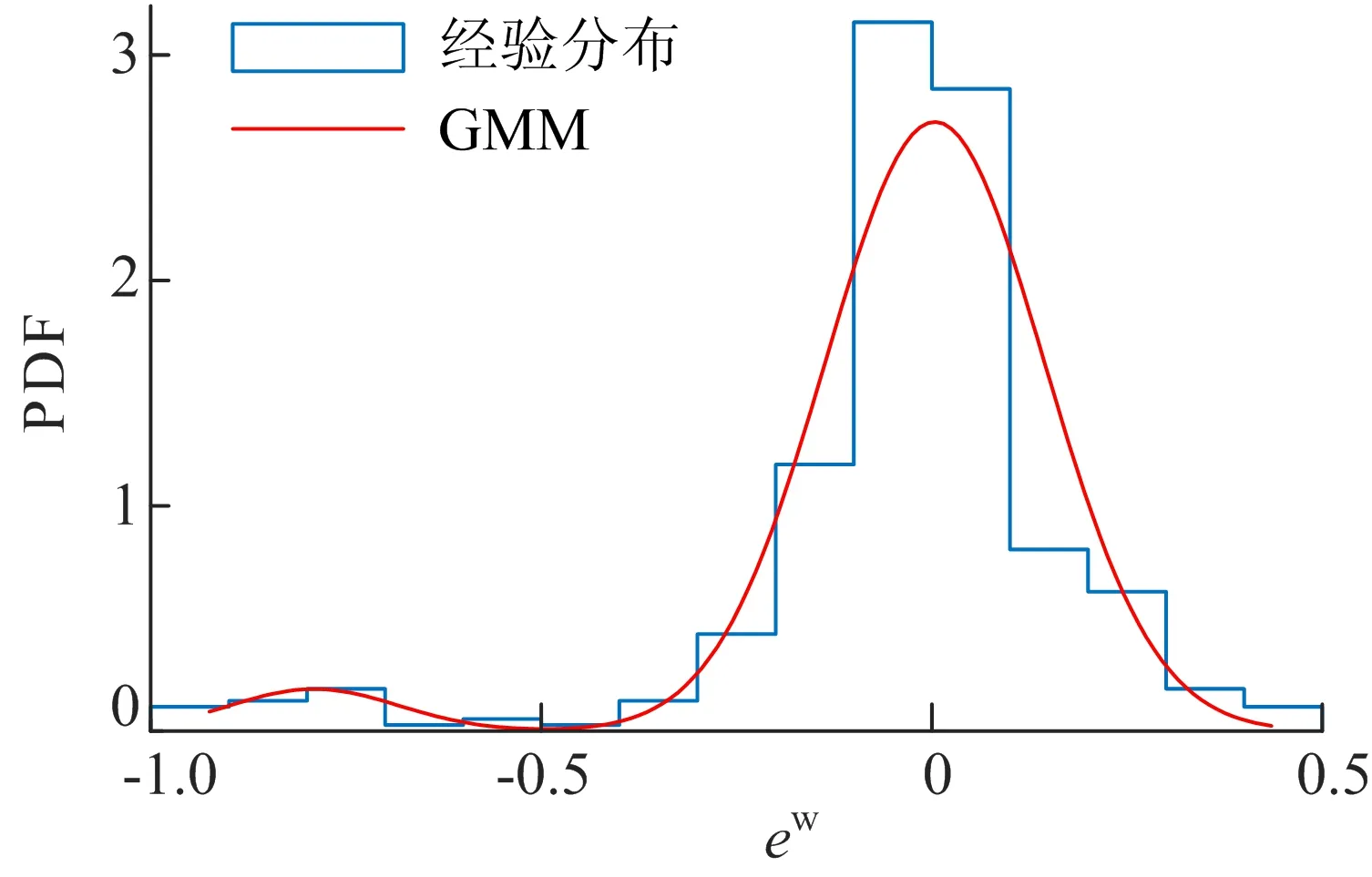
图2 光伏出力预测误差的PDF

GMM方法对多峰分布的描述具有优势,这是Beta分布所不具有的。

以所提互补模型优化2018年7月1日的日出力曲线,设置三光伏电站的出力设定值从装机容量的30%增长到100%,不考虑DE算法优化。各个光伏电站平均出力、平均备用需求以及总社会效益的变化情况如图3所示。

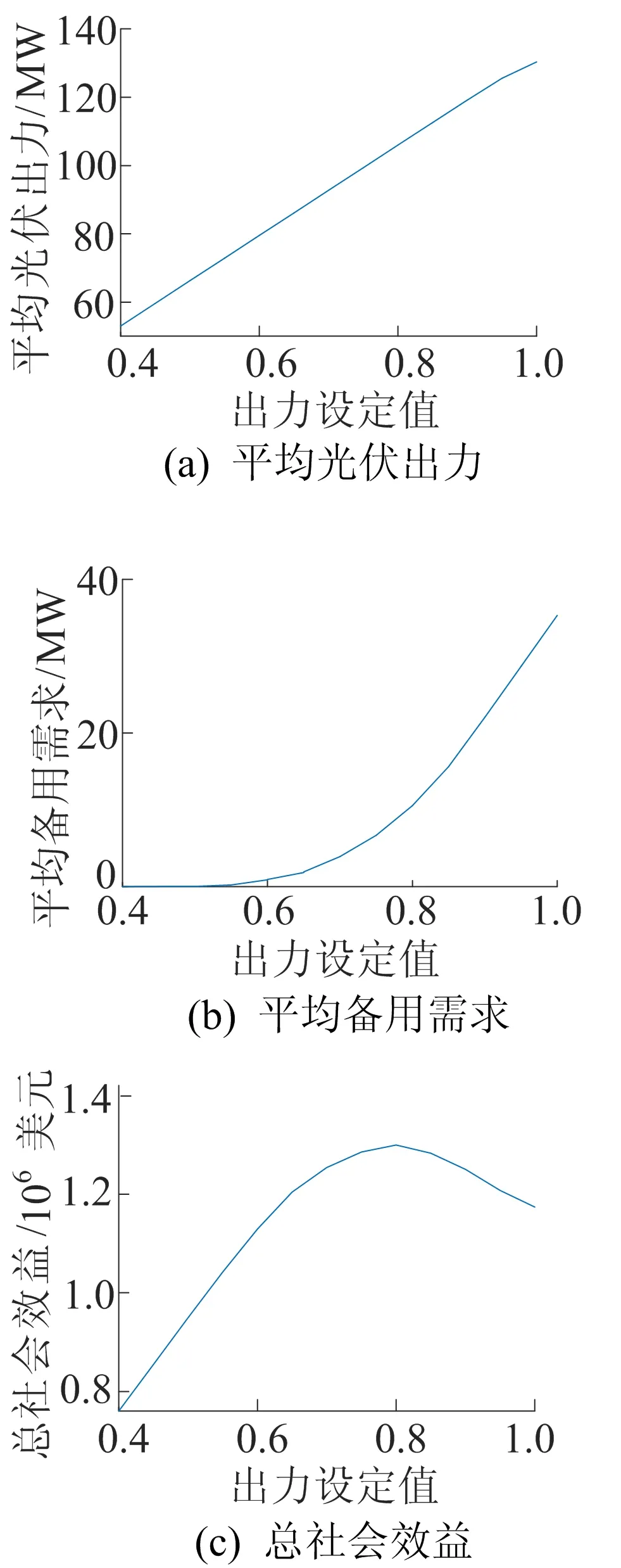
图3 出力设定值对光伏出力、备用需求以及总社会效益的影响

由图3可知,随着出力设定值的增大,发电量与备用需求同步增大。设定值越大,各光伏电站的降额比例越低,其出力特性也就越接近调整前的状态,发电量与备用需求同步增加。根据(10)式,总社会效益等于光伏发电收益减去备用购买成本,因此在图3中的设定值变化范围内,存在出力设定值组合使得总社会效益最大,求解最优出力设定值具有可行性。

采用所提最优出力设定值算法得到优化后的日出力曲线如图4所示。如果为各光伏电站提供100%备用,那么完全可以做到0弃光,但需要支付高额的备用成本。本文算法综合考虑光伏发电效益与备用成本,令光伏电站适度弃光,以降低备用需求。优化前后的总社会效益分别为1.16×106、1.38×106美元。图4中3个光伏电站平均弃光率为5.82%,最大弃光功率为27.34 MW。弃光现象在光伏出力较大时相对明显。降额运行同时降低了多光伏电站联合系统对于备用的需求,进而降低备用成本。从电网角度来说,降低了整体的运行成本。

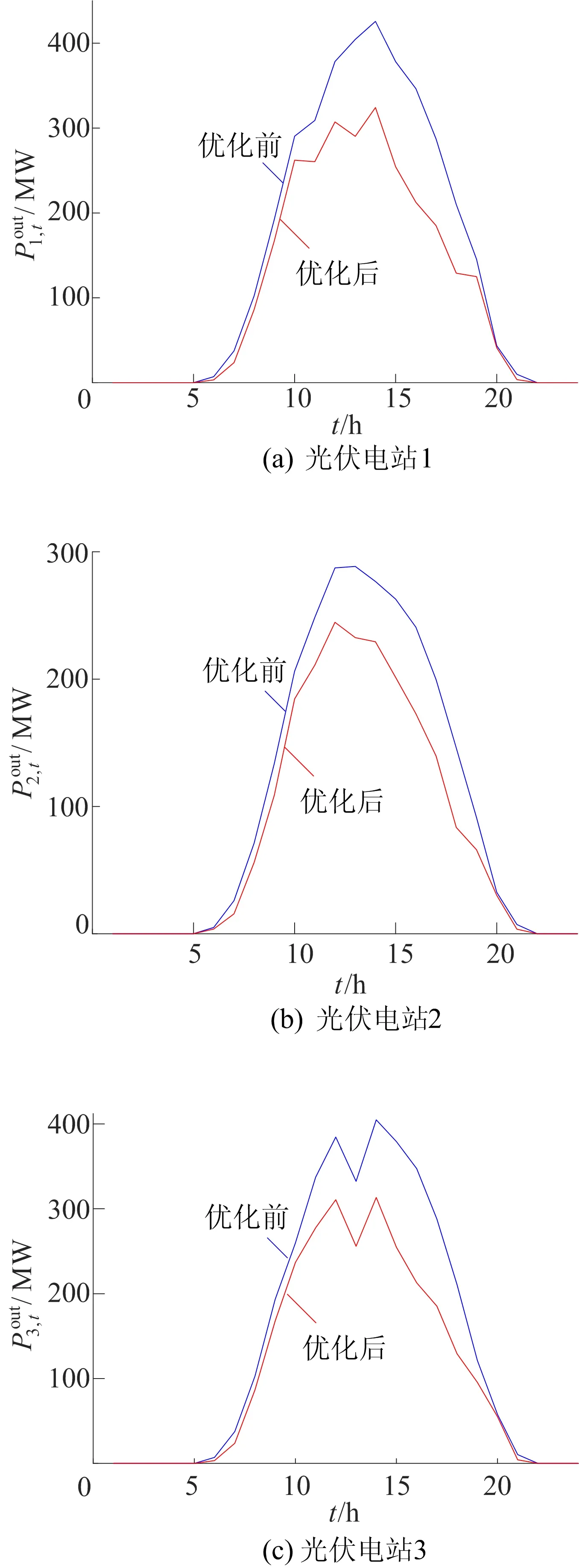
图4 优化前后光伏电站出力曲线

采用最优出力设定值的互补模型与直接按照预测误差满足置信度2种方法得到的备用需求如图5所示。

备用需求与光伏出力正相关,光伏出力越高,备用需求越大。优化后的光伏电站备用需求明显降低,总备用需求相比优化前降低70.05%。甚至在9、10、11时段,光伏电站的备用需求为0。由于降额运行,这些时段的实际出力已经满足供电安全置信水平,不再需要额外的备用。

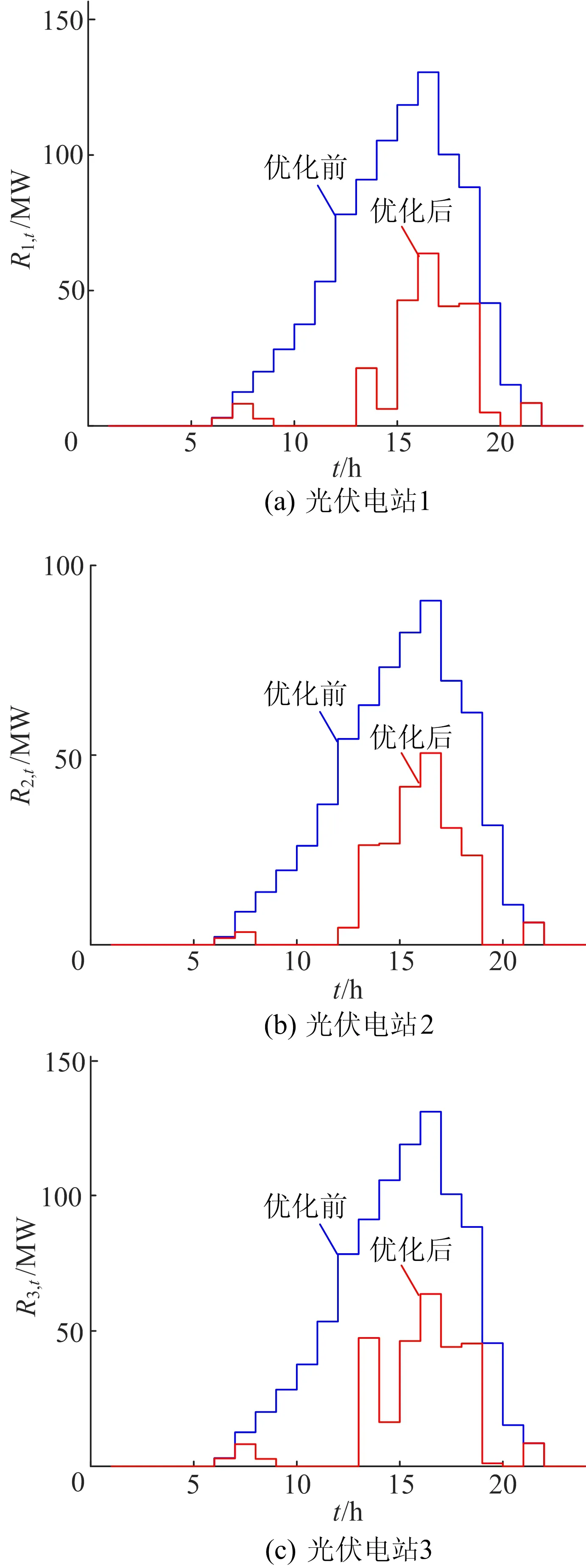
图5 光伏电站备用需求

4 结 论

本文建立适用于多光伏电站的互补模型,实现多光伏电站间有功出力的降额运行。同时在分析光伏电站有功出力特性、备用容量需求以及总社会效益的基础上,提出了混合差分进化算法求解最优出力设定值,解决了互补模型中出力设定值参数选取困难的问题。

仿真算例证明了本文所提出的多光伏电站互补模型能够在满足供电安全可靠性约束的条件下,有效降低光伏电站的备用需求,提高光伏电站的总社会效益。同时,本文提出的最优出力设定值算法为制定光伏出力生产调度计划提供了充分的理论支持。