OU过程下方差互换的定价问题研究

贾兆丽,杨舒荃,吴霍俊

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

波动率衍生品作为一种特殊的金融衍生品,其价值依赖于将来波动率的期望水平。随着人们对风险控制和对冲的需求不断增加,波动率衍生品的交易受到越来越广泛的关注。目前,交易最活跃、最普遍的波动率衍生品是方差互换和波动率互换。

自20世纪90年代末以来,有许多学者致力于研究合适的方法来定价方差互换。在连续取样方面，文献[1]首次提出了自由偏好随机波动模型,并用于普通的方差互换及奇异的波动率衍生品定价中;文献[2]利用非参数方法研究了基于对数合约下方差互换的Delta对冲策略;文献[3]分析了3/2随机波动率模型下,通过连续取样合理近似离散取样的互换的定价问题,并给出了连续近似存在的条件。实际操作中,连续选取标的资产的实际变差可能会对互换产品的定价带来系统偏差。用高频的数据来估计定价公式,会由于小的样本取样或是大的分割而导致更大的误差。

在离散取样方面,文献[4]推导出在随机波动率模型为Heston模型下的方差互换的闭型定价公式;文献[5]分析了Heston随机波动模型对波动率衍生品远期价格的影响,并提出了一种新的研究方法,即将服从对数正态分布的方差与随机波动率的二次变差相结合;文献[6]研究了一种时齐随机波动率模型下方差互换的远期价格,得到了离散取样的方差互换的近似定价公式。在跳扩散模型下,文献[7]得到了条件方差互换和Corridor方差互换等几种方差互换衍生品的定价公式；文献[8]结合体制转换模型、马尔科夫链近似方法和傅里叶变换,提出了一种投影方法来计算波动率衍生品的价格。此外,还有文献[9-12]阐述了几种随机波动率模型对方差和波动率互换定价的影响。

本文主要采用积分变换的研究方法,计算实际波动率(方差)的特征函数及衍生品的支付函数的积分变换。在离散取样的基础上假设随机波动率服从OU过程,并利用微分方程求解方差互换的远期价格,最终得到方差互换等波动率衍生品的定价公式。

1 方差互换

方差互换是众多互换产品的一种,它是一份远期合约,收益基于标的资产指数的实际变差。该资产指数可以是标普500或是NASDAK指数等。合约买方从签订方可获得的收益,取决于整个合约期内实现的资产指数方差与合约签订时敲定方差的差值, 偿付额为一设定的单位乘数与此差值的乘积,即

(1)

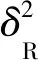
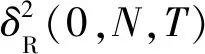
(2)

(3)

其中,Sti为在第i次观测时间ti时刻的股票价格;T为合约到期日;k为年化因子,若取样频率是每一个交易日,假设每年有252 d为交易天数,则k=252;若每周为取样频率,则k=52;若每月为取样频率,则k=12;以此类推。本文只考虑等距离散观测,即Δ=ti-ti-1为常数, 总共观测N次,ti=iΔt(i=1,…,N)。为了模拟的方便,将实际变差乘以名义本金M,且取M=10 000。

2 方差互换的定价

2.1 模型建立

设(Ω,F,Ft,P)为概率空间,Ft,t∈[0,T]为自然域。假设存在风险中性概率测度Q,且随机波动率服从均值回复OU过程,用St表示股票价格过程,其瞬时波动率记为vt,满足的随机微分方程如下:

(4)

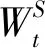
2.2 主要结果与证明

本文采用微分方程求解方差互换的远期价格,离散情况下的实际变差由第2种定义 (3) 式给出。

定理1 当波动率服从OU过程,动态资产价格过程满足方程(4),则方差互换的敲定价格KVar有如下形式:

(5)

其中

g(v0)=(E(1))2v4+2D(1)E(1)v3-[(D(1))2+

2C(1)E(1)+E(2)]v2-(2C(1)D(1)+

D(2))v-(C(1))2-C(2)；

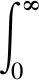
(C(1))2-C(2)，vti-1=v；

证明由实际变差的定义可知,要计算方差互换的远期价格,就是求N个的期望，即

(6)

假设Δt为常数,ti=iΔt(i=1,…,N)。问题转化为求下列2个微分方程的解,在没有特别说明的情况下,计算过程中i、ti及ti-1认为是已知的常数。

(7)

(8)

其中

由Fourier变换性质有:

F[xn]=2πjnδ(n)(ω)

(9)

由Dirac函数的性质可得:

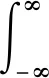
(10)

令x=lnS,则方程(7)变为:

(11)

在方程(11)中,对支付函数两边关于变量x进行Fourier变换,得:

F[(x-lnI)2]=2π[-δ(2)(ω)-

2jδ(1)(ω)lnI+δ(ω)ln2I]

(12)

方程(7)的解为:

P=F-1{exp[C(ω,ti-t)+D(ω,ti-

t)v+E(ω,ti-t)v2]×

2π[-δ(2)(ω)-2jδ(1)(ω)lnI+δ(ω)ln2I]}=

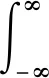
E(ω,ti-t)v2]×[-δ(2)(ω)-

2jδ(1)(ω)lnI+δ(ω)ln2I]exp(jxω)dω=

-h(2)(0)+2jh(1)(0)lnI+h(0)ln2I

(13)

其中

h(ω)=exp[C(ω,ti-t)+D(ω,ti-t)v+

E(ω,ti-t)v2+jxω]

(14)

通过计算(14)式的一阶、二阶导数可得:

(15)

其中

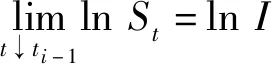
(16)

其中

g(v)=(E(1))2v4+2D(1)E(1)v3-

[(D(1))2+2C(1)E(1)+E(2)]v2-(2C(1)D(1)+

D(2))v-(C(1))2-C(2);

同理D(1)、D(2)、E(1)、E(2)也有类似定义。

方程(8)的解为:

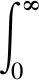
g(vti-1)p(vti-1|vt)dvti-1

(17)

其中,p(vti-1|vt)为OU过程的概率转移密度。

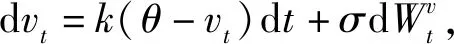
θ(1-exp(-k(T-t))),

(18)

(6)式的期望可以表示为:

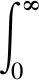
(19)

(19)式的计算可以通过一般的数学软件来进行,从而可以求出方差互换的远期价格，写成以下较为简单的形式:

(20)

其中

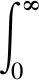
(C(1))2-C(2)，vti-1=v；

综上,可以得到方差互换的远期价格为:

(21)

3 结 论

本文假设标的资产的价格服从随机波动率模型,通过交换积分次序,利用广义的傅里叶变换方法,得到了密度函数的积分变换及支付函数的积分表达式。在离散取样下,给出了随机波动率服从OU过程时方差互换的定价公式。该结果丰富并发展了金融衍生品的定价理论,同时可以应用于其他金融衍生品的定价,为资产定价理论的研究提供了新的模型。