三维动态海面高频段雷达回波多普勒谱分析∗

（西南电子技术研究所 成都 610036）

1 引言

在微波遥感中，天波超视距雷达利用海洋表面对高频（High Frequency，HF）电磁波的散射机制，可以从雷达回波中提取海面风场、浪场、流场等海况信息，从而实现对海洋环境大范围、高精度和全天候的实时监测。国内外众多学者对天波超视距雷达的海洋回波谱进行了各种实验和理论的研究。焦培南等[1]采用实验方法，研究了高频天波返回雷达对地面及海面的多普勒回波频谱特性，以及电离层状态、风向、海流等参数对多普勒频谱的影响。针对高频天波超视距雷达盲区问题，国内学者提出采用天波地波混合体制雷达观测海杂波特性的方法，并对每种特性进行了详细的分析和解释[2～3]。由于采用实验方法研究高频天波超视距雷达海面的散射多普勒频谱，容易受到电离层污染的影响以及实验硬件条件的限制，且成本高，可重复性差，因此有必要开展对海面多普勒频谱的数值仿真模拟研究。因此，本文提出了海面雷达多普勒频谱的数值仿真模拟方法，进而研究三维动态海面在高频波段的雷达回波多普勒频谱特性，并解释了相关雷达回波特性与海面散射机理。

2 三维动态海面几何建模

海浪谱是描述海浪、揭示海浪内部结构最有力的工具之一。在大量的实测海浪谱研究中，以Pier⁃son-Moskowitz（PM）谱应用最为广泛。PM谱是Pierson，Moskowitz等通过对北大西洋上1955年～1960年的观测资料进行分析得到的无因次谱[4]，大量的海面数据统计表明，PM谱能很好地表征真实的充分成长的风场海面波。

通常，三维动态海面可以采用谱快速傅立叶变换（FFT）方法得到。其中，带有各向异性的扩展因子的二维PM谱可表示为

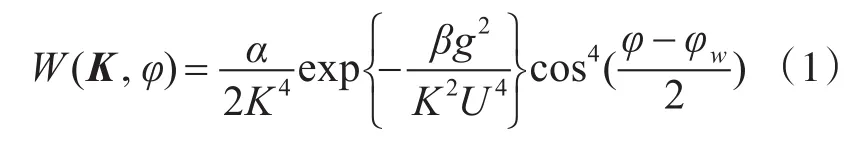
U(m/s)是海面上方19.5m处的风速，α=8.1×10-3，β=0.74为常数，g=9.81m/s2为重力加速度，K=|K| 为空间波数，其中，K=(Kx，Ky)=(Kcosφ，Ksinφ)，φw为风向。

动态随机海面的产生过程则有以下几个步骤：首先产生一组正态分布的复随机序列R(K)；然后依式（2）求得空间傅里叶变换分量S(K，t)；最后由IFFT得到三维动态海面每个点的高度。

3 多普勒频谱分析

3.1 准静态方法

准静态方法将动态海面在时间间隔τ内看成静止的（准静态），且入射波视为连续波，近而采用频域方法求解某时刻静止海面的电磁散射特性[5]。Toporkov对准静态方法的基本原理做了详细的解释，一般来说，在时间间隔τ内海面的变化不能太明显，满足如下关系：，其中Cp是主波的相速，决定了海面的水平面的运动速度。对于PM谱海面来说，Cp可由式（3）得到。

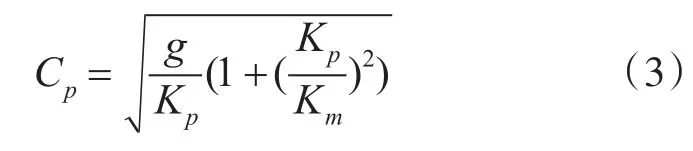
同时，时间间隔需满足τ>2L c，L为海面长度，c为电磁波传播速度，以保证照射到海面上的电磁波可以视为连续波且波形不会出现畸变。

3.2 蒙特卡罗法仿真

对于随机粗糙海面，需要进行蒙特卡罗法仿真，以此得到海面电磁散射特性。综合多种电磁仿真方法的计算资源要求，本文采用快速的近似方法来分析动态海面的电磁散射。

海面被离散为三角小贴片，设n̂为三角贴片的外法向矢量，为入射电磁波的方向矢量，则海面的照明区和阴影区可用简单的方法来判断：当时，为暗区，反之为亮区。基尔霍夫近似认为暗区的电磁流均为0，只有在亮区存在电（磁）流。定义小面元的水平极化方向为，垂直极化方向为。由Fresnel式（6）可知小面元处得反射系数RH（水平极化）和RV（垂直极化）为

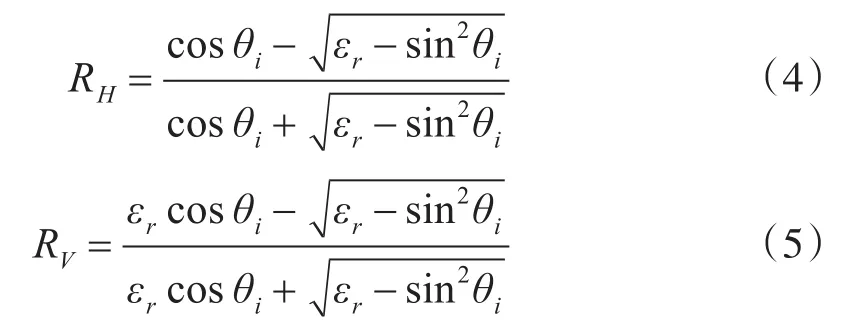
式中θi为小面元的局部入射角，可根据公式求得，εr=73.0-5375.8i为 15MHz时海水的相对介电常数，其中。设入射电场为，则磁场其中，k=2πλ，λ为电磁波长，η0=120π为自由空间中的特征阻抗。亮区表面感应电磁流可由以下公式得到

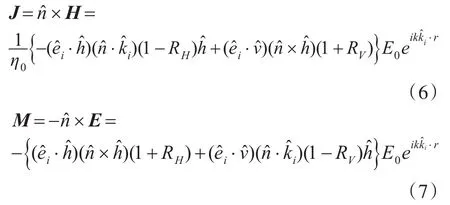
H为海面上的总磁场，E为总电场。从海面表面电磁流可得远区散射电场为

T为观测时间。由于海面的随机性，一次海面演进过程中所得到的雷达多普勒频谱同时含有这些随机因素的影响，采用蒙特卡罗法即多次求解取平均的方法来考察动态海面的多普勒回波的统计特性。N次宗量平均的多普勒频谱为

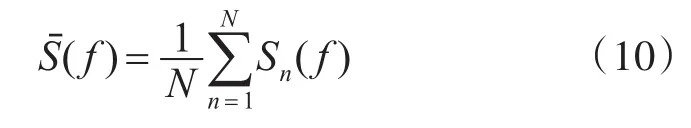
上述过程完整的描述了蒙特卡罗法求解动态海面雷达回波多普勒频谱的方法。

4 计算结果及分析

在对海面的仿真计算中，雷达频率设置为15MHz，采用垂直极化方式。

4.1 Bragg散射机理

Bragg散射的根本原因是波浪间后向散射电磁场回波的相干叠加[8]，如图1所示。只有当海浪波长 Λ，电磁波长λ以及入射角度θi满足条件Λ=nλ/2sinθi下才会产生，n为正整数。波浪间的电磁场后向散射回波相位相差2π的整数倍，产生相干叠加，后向散射明显增强。在HF频段，海浪波长和雷达波长相比拟，Bragg散射对雷达后向散射影响很大。

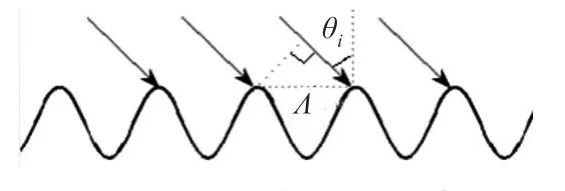
图1 Bragg散射机理示意图

为说明电磁仿真对海面信息的敏感性，采用海浪波长满足Bragg散射条件的组合正弦波海面：，海面沿x轴的正向传播，两个正弦波分量的传播速度分别为5m/s和7m/s，大小设为200m×160m。依据上述时间间隔的选取规则，采用时间间隔τ=0.2s，观测时间T=40s。取 Λ=λ，以满足Bragg谐振条件。当入射角为30o时，此海面的多普勒频谱如图2所示，可见两个最高的峰值分别位于-0.25Hz和-0.35Hz，对应于两个正弦分量的运动速度，与理论值吻合。

4.2 动态海面的多普勒频谱

海面可以看成是由一组不同频率，不同相位，不同速度的正弦波相互叠加而成，因此在每一入射角度下，都会有和入射电磁波产生谐振的频谱分量，这一频谱分量的后向散射产生相干叠加，反应到多普勒频谱中即为Bragg峰。

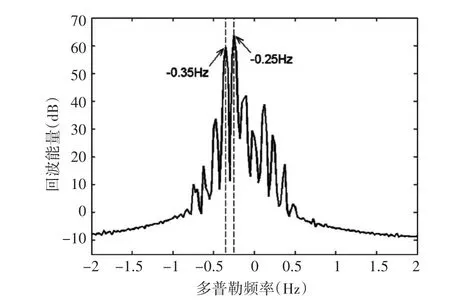
图2 组合正弦海面的多普勒回波

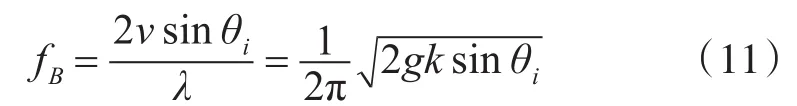
海面大小设置为840m×120m，时间间隔τ=0.2s，观测总时间T=40s。采用蒙特卡罗法，产生50组不相关的随机动态海面，求得其平均多普勒频谱。图3为海面上方风速分别为7m/s，15m/s情况下雷达照射角度分别为30°，40°，50°和60°时雷达多普勒频谱。随着入射角度的增加，回波电平降低，Bragg峰愈加明显，这说明在海面散射机制中镜面散射是主导地位，随着角度的增加，Bragg散射对后向回波的叠加效应成为雷达回波的主要因素。

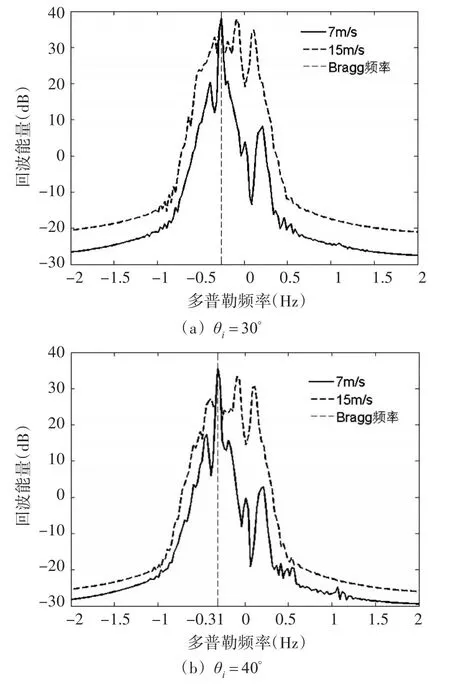
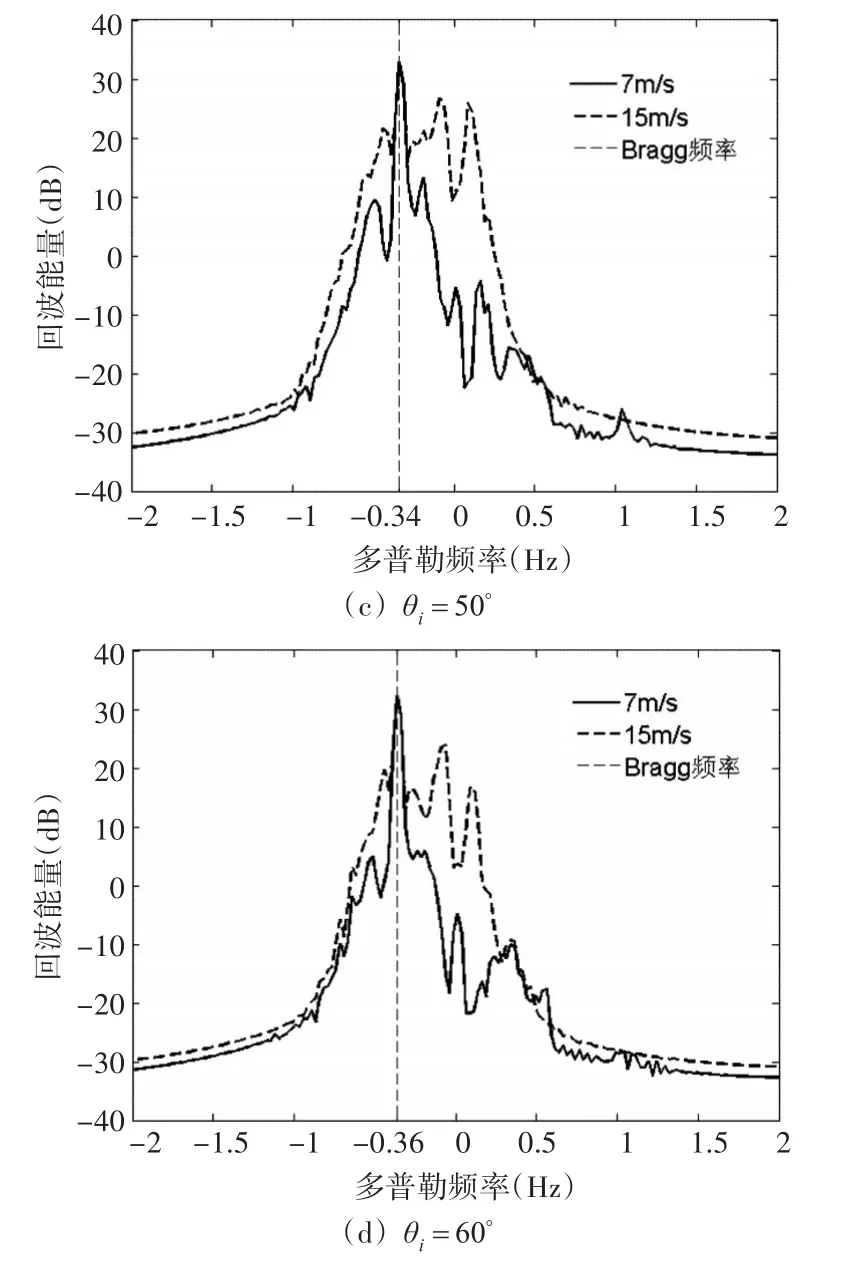
图3 典型动态PM海面的雷达回波多普勒频谱

通过图3的实验对比发现：随着风速的增大，海面的雷达多普勒回波频谱呈现出展开效应。这是由于PM谱海面是传播特性不同的正弦形式简单随机波动波叠加而成，其各分量波的运动速度也不尽相同，且海面各点随时间振动，非相干散射增强，由此反映到海面多普勒回波谱中导致频谱展宽效应。因此，在对各向异性的风场海浪监测中，雷达回波的多普勒域信号更为复杂，对目标的检测更加困难。

5 结语

针对高频天波超视距雷达电磁仿真问题，将准静态方法引入到高频天波超视距雷达下的三维动态海面回波频谱的研究中，解释了Bragg散射的产生机理，通过与正弦海面的回波频谱对比，证明由海面的随机性而导致的非相干散射是使得频谱展宽的主要原因。本文研究为天波超视距雷达系统对海监测提供了重要的理论基础和必要的技术手段。