基于自适应滤波的光纤惯性陀螺仪降噪技术研究∗

（昆明船舶设备研究试验中心 昆明 650051）

1 引言

光纤陀螺仪（FOG）作为测量惯性角速度的一种常用敏感元件，已成为捷联惯性导航系统不可缺少的新型设备[1]。它具有体积小，全固态，重量轻，动态范围大等特点，已被广泛应用于许多领域。使其在航空航天以及航海领域上得到了充分的重视[2]。该系统检测的Sagnac相移是在信号传导过程中微小有用信息量，很容易被噪声干扰。所以采用快速有效的算法对信息进行滤波减弱噪声影响，对改善陀螺系统整体性能具有重要作用。

对于消除噪声，通常采用光纤传导路径和电路滤波这些方式，然而采用数字滤波消除随机噪声也是重要方法[3]。文献[4]采用卡尔曼滤波的方式，但此方法的收敛快速性不能适应系统快速反应的要求。文献[5]运用神经网络算法，仿真效果良好但难以在实际工程中实现，文献[6]运用NLMS算法的自适应滤波方法，但滤波阶值的设置对效果影响太大。本文运用新的LMS算法融合自适应滤波器来降低噪声。在保证系统快速性需求前提下获得最优参数，收敛性能及降噪效果均好于普通的LMS算法，对去除光纤陀螺噪声影响具有重要意义。

2 光纤陀螺噪声机理及LMS算法

2.1 光纤陀螺噪声来源

光纤陀螺的输出含有大量统计特性可近似为白噪声的噪声项[7]。其中主要有光源相对强度噪声、散粒噪声、电阻热噪声、信号量化噪声、热相位噪声以及其他环境因素的扰动引起的噪声[8]。按照产生原因大致可包含在以下三个过程中：光路传播过程、信号检测过程、环境扰动。

2.2 Allan方差噪声分析

相关论文曾作出验证[9]，频域上σ2(τ)与输出功率谱密度呈线性相关：

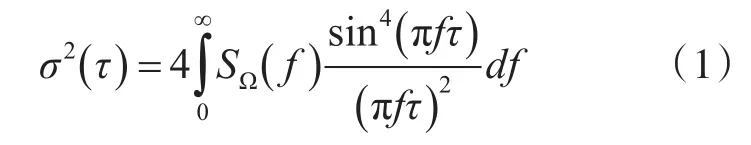
通过此种方式，可以迅速分辨系统输出信息保含的各种特性噪声项及量化。即角随机项、量化噪声、偏置不稳定性、速率斜坡、速率随机项等。如图1所示。

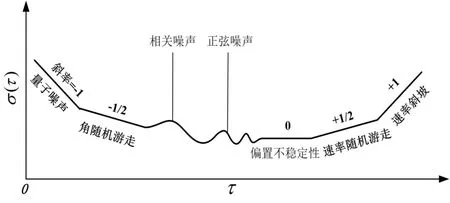
图1 Allan方差分析各种噪声项

2.3 分数变阶数LMS算法

最小均方差（Least Mean Square，LMS）算法是结构简单且工程性好的算法[10]。分数变阶数LMS算法（Fractional Tap-length LMS，FTLMS）是Gong在2005年提出的[11]，突破阶值总是在整数间变化的限制，把分数累加后进行更新。对代价函数做一定改进，增强算法自适应性，减小计算量。大大提高了算法的收敛速度。在FTLMS算法中阶值误差方程在片段误差平方值来定义[12]，如下式：

分数阶数记作lf(n)，其更新过程是：

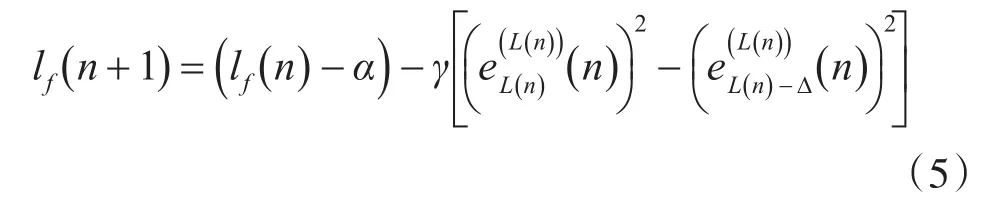
式子里γ是阶数迭代步长。α为泄露参数。其值选取不能超过一定值，减缓收敛速率。其数值远小于γ。算法更新过程中，lf(n)分数值作累积取整，其表达式为

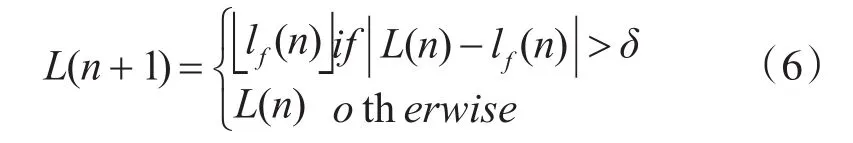
式中，μ为权值系数的更新步长。

FTLMS分数阶值细化了阶值定义，拓宽了该方法应用范围。

2.4 变迭代参数的FTLMS算法

对上节算法作一些调整，即使参数也随系统改变，称之为变参数FTLMS算法（VP-FTLMS）。根据上面叙述，式（5）可以写成：

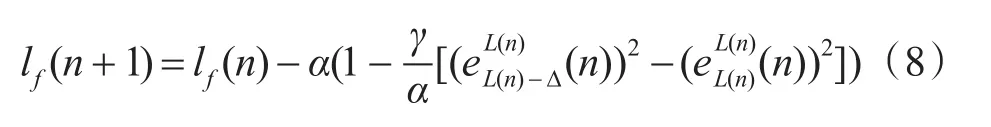
因为α>0，容易看出α/γ比值，即α/γ会较明显影响阶数收敛性。上文已知α<<γ，γ一定时，α取值基本不影响α/γ。γ作为迭代参数，γ值与收敛速率正相关，与稳态性负相关。所以，γ值是协调收敛速率与稳态性能的重要因素。故引入一个新变化量g，用于使参数γ可调整。本文以额外平均方差意义下定义此变化量。称为改变参数的FTLMS算法，简写为VP-FTLMS算法。

从LMS算法理论方程可知，瞬态误差即：e(n)=ζ(n)+t(n)，t(n)为系统噪声，ζ(n)为迭代噪声，则：

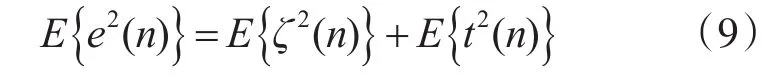
上式中，E{e2(n)}是平均方误差（Mean Square Error MSE），E{ζ2(n)}为额外均方误差（Excess Mean Square Error，EMSE）。E{t2(n)}系统噪声均方值。因为EMSE在系统稳定之后趋向零，符合滤波的迭代进程，所以运用EMSE改变迭代参数[13]。EMSE估计表达式为

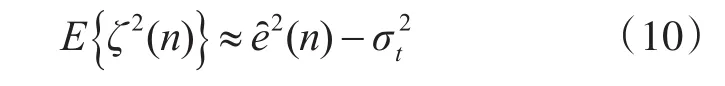
式（11）平滑系统瞬时误差，消除误差项震荡影响。g是新定义可改变量，式中用瞬态额外均方差与初始值与瞬态值和的比值来表达。式中的ρ是平滑输出误差方差的参数，ρ≤1。在（13）中γmax代表迭代步长γ稳态所得值。

则改进后系数的更新方程是：

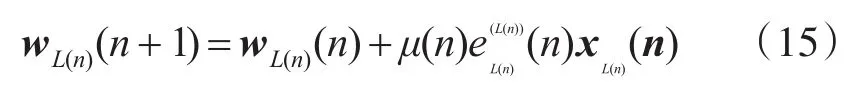
其中L(n)是取整阶数。

3 自适应降噪方案设计

3.1 前向线性预测

线性预测指运用数据中已得知量线性估计数据序列中未知量。一步预测即利用数据序列一组连续值往前或者往后线性预测估计一个量。这里用某时刻之前M个量，预估出在此之后的量，就是前向一步线性预测[14]，即前向线性预测滤波器（Forward Linear Prediction Filter，FLP Filter）。

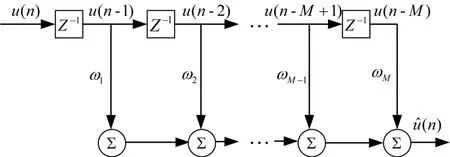
图2 FLP滤波器基本结构图

在此基础上的自适应滤波模型框图如图3。

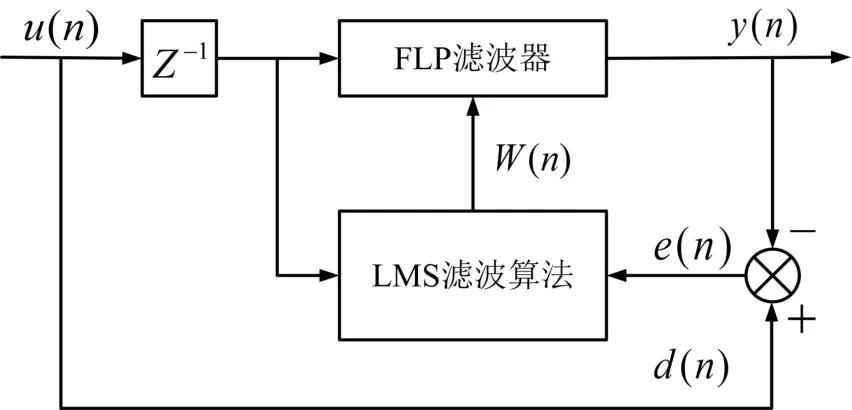
图3 自适应滤波模型图

时刻n的输出采样为u(n)，滤波阶数为L。输入即u(n-1)，u(n-2)，…，u(n-L)，记作向量形式为U(n)。L×1维的向量即权值系数W(n)。则y(n)为当前时刻整体输出值u(n)的估计û(n)，则即：

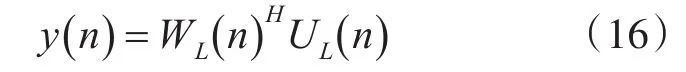
目标响应函数d(n)即等于u(n)，则：

根据以上理论基础，运用前向线性预测作为自适应滤波的主要结构来减弱系统噪声，而权值计算方法融合新的VP-FTLMS算法。

3.2 自适应滤波器

自适应滤波器优势在于根据条件变化相应改变参数始其收敛于最优解，此过程并不改变自身结构，易工程实现。运用最优解反馈到FLP滤波器，从而获得系统信息估计。

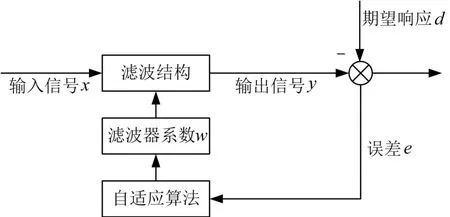
图4 自适应滤波器结构图

本文以光纤陀螺去除无用信息前提下应用自适应滤波，其算法融合新的变化参数算法（VP-FTLMS），以期得到滤波阶值最优，对输出信息作出较好估计，从而达到系统噪声抑制的目的。

4 实验与分析

实验数据采用精度0.01°/h陀螺仪X轴方向输出的真实数据。根据前文理论获得最优参数，将α取值是0.001，γ取值是经验值0.04，∆可以选为2。滤波器μ取值是0.05，阶值初始值定为5。基于FT-LMS滤波阶数的收敛过程如图5所示。

图5 滤波器阶数收敛图

可以看出，阶值自初始设定5逐渐收敛到30，即得到最优解为30。进而选取五种阶值，对比其作用效果得出最优阶值收敛性。将阶值分别选定在30附近相差10的位置，其他初值保持相同。将原始输出数据通过五个阶数不同的滤波器后的输出对比结果如图6所示。

图6 五种阶数值的作用效果对比

通过数据可明显看出，在数字滤波过程后，有效去除了大量无用信息。这种滤波作用与阶数值成正相关，当阶数超过某临界值后，则不再明显变化。

下面将FTLMS与改进VP-FTLMS在收敛快速方面进行比较，如图7所示。

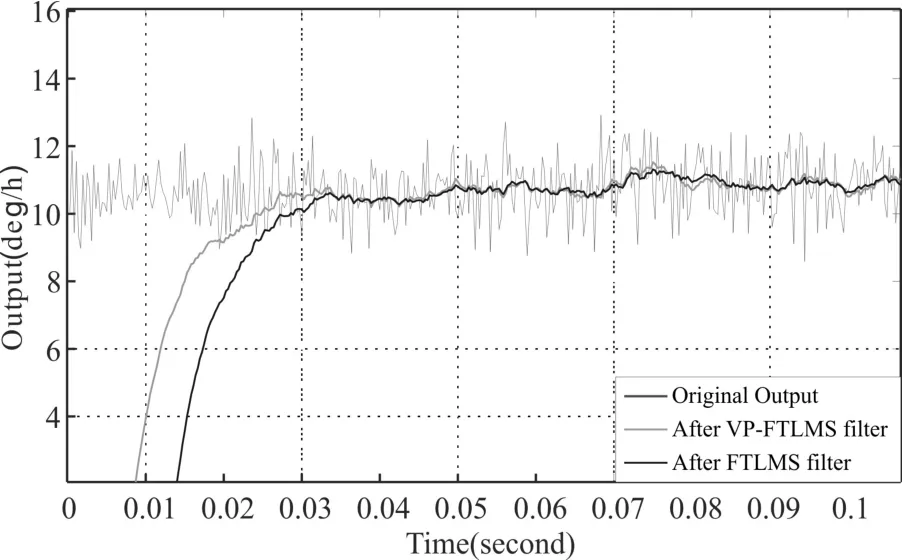
图7 FTLMS与VP-FTLMS收敛性能对比

由上面分析可得，VP-FTLMS算法比普通变阶数收敛灵敏性有了很大提升。在真实数据上也得到了验证。说明新方法理论上的正确性和实际应用可行性。改进的算法能够根据系统输出信息之间的相关性，将有用信号从输出信号中提取出来，进而达到降低系统输出噪声的目的。较好地体现了融合新算法的动态跟踪性能，快速去除了系统输出过程中包含的大量无用信息，对进一步改善惯性导航系统具有一定工程意义。

5 结语

本文在详细的惯性器件输出的噪声理论分析基础上，针对输出信息中角随机游走项，运用了改进LMS的方法降低系统输出信息中的无关量。以VP-FTLMS作为融合算法获得参数最优值，运用真实测得的数据进行了算法实验，验证了该方法得出最优参数正确性，能够看出融合VP-FTLMS改进算法具有较好滤波效果。有效地从系统输出噪声中提取出需要的微小信息，一定程度提高整体的精确性，对惯性系统进一步提高具有工程意义。